Probas xeométricas

1993/06/01 Angulo, Patxi Iturria: Elhuyar aldizkaria

• Matematika

O teorema de Pitágoras non é o único que pode demostrarse por xeometría. Moitas das similitudes e diferenzas matemáticas pódense contrastar utilizando figuras xeométricas. Neste artigo presentámosche algunhas delas.

A primeira figura mostra a verificación xeométrica simple dunha das fórmulas básicas:

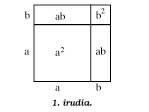
(a + b)2 ⁼ a2 + ^2ab + b2

Na segunda figura si é similar á fórmula anterior

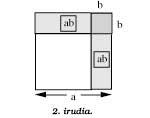
(a - b)2 ⁼ a2 - ^2ab + b2

trátase da expresión xeométrica correspondente á fórmula. Obsérvese que o cadrado ^{correspondente ao sumando} b2 está dentro do rectángulo correspondente ao sumando ab e que ao cadrado a2 quítaselle ^dúas veces ( -2ab).

^Si na figura ² extraemos o cadrado b2 polo cadrado a2 (figura 3), a superficie trazada, 2ab, non cambia. Agora obsérvase a seguinte diferenciación:

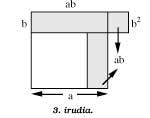
2ab a2 ⁺ b2

Continuando coas diferenzas, a figura 4 mostra a demostración xeométrica doutra diferenciación equivalente á anterior:

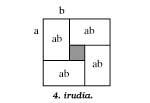
4ab (a + b) 2

Calculemos agora a suma con infinito sumando (Figura 5). Engadindo a metade ao cadrado ao lado 1 obtemos 1 + 1/2 = 3/2. Sumando a esta suma a cuarta parte do cadrado temos 1 + 1/2+ + 1/4 = 3/2 + 1/4 = 7/4. Engadindo un oitavo a este último 1 + 1/2 + 1/4 + 1/8 = 7/4 + 1/8 = =15/8. Como se pode apreciar na figura, esta suma é inferior a 2. O seguinte sumando 1/16 pódese introducir no oco que está baleiro. No oco que queda sen cubrir sempre poderemos incluír todos os sumandos seguintes. Finalmente cubriremos o rectángulo 1x2. Por tanto,

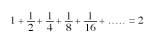
Conseguiremos a igualdade. Os puntos que aparecen nesta igualdade indican que está infinito sumando.

Pasando a outra fórmula, calcularemos a suma dos primeiros números. Paira iso utilizaremos os cadrados básicos. (Ver figura 6).

Si continuamos así, calcularemos a suma dos n primeiros números (ver figura 7).

1 + 2 + 3 + ... + n = n (n + 1)/ 2.Utilizando

cadrados básicos podemos probar outras fórmulas. A figura 8 móstranos que as sumas dos números impares son números cadrados.

Que pasa cos números pares?. Imos velo.

A suma dos números pares non forman cadrados, senón rectángulos. (Ver figura 9).

Esta é a expresión xeométrica doutra nova fórmula.

Terminaremos coa explicación xeométrica doutra fórmula máis complicada:

13 ⁺ 23 + ³³ +... ⁺ n3 == (1 + ² +
3 + ... + n)2

a fórmula.

Seguindo a liña das expresións das fórmulas anteriores, obtemos a seguintes igualdade:

13 ⁼ 113 +
23 ⁼ 9 = ³² = (1 + 2)213 ⁺ 23 + 33 = ³⁶
= ⁶² = (1 ⁺ 2 + 3)213 ⁺ 23 + 33 ⁺ 43 = 100 = 102 = ⁽¹
+ ² + 3 ⁺ 4)2

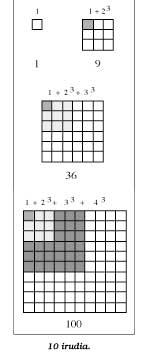
e xeneralizando os resultados conseguiriamos dita fórmula.