Quan la ficció es fa realitat

2014/05/01 Azkune Galparsoro, Gorka - Ikertzailea eta irakasleaEuskal Herriko Unibertsitateko Informatika Fakultatea Iturria: Elhuyar aldizkaria

• Fisika
• Sariak

Quàntica, sempre quàntica

La idea científica que més s'acosta a la mena de teletransporte que hem vist en sèries com Start Trek és la teletransporte quàntic, l'objectiu del qual és transportar un sistema quàntic des del punt A fins al punt B, sense cap mena de suport o canal físic. Però per a entendre tot això correctament hem d'explicar algunes de les bases de la física quàntica. No t'espantis! Perquè ho farem d'una manera molt senzilla.

Caixes i boletes

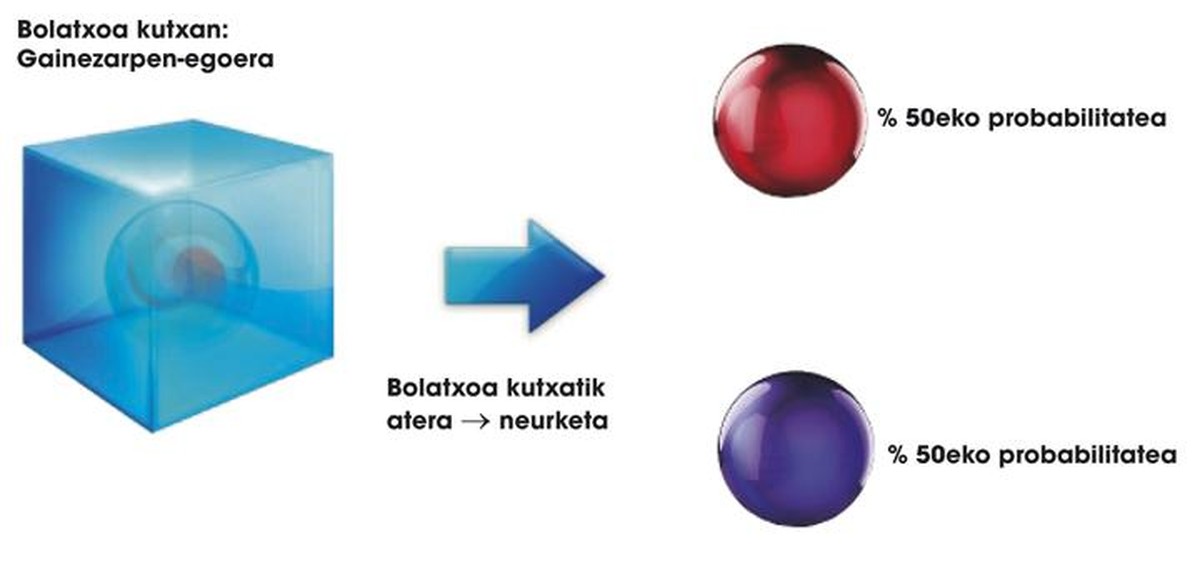
Quan parlem de sistemes quàntics parlem de conceptes com a àtoms, electrons, protons o fotons. Per a facilitar les coses, els sistemes quàntics seran unes boletes especials guardades en unes caixes especials. Aquestes boletes poden tenir dos colors: vermell | G> o blau | O>. La primera peculiaritat d'aquestes boletes és que, mentre romanen a l'interior de la caixa, poden estar en un estat de combinació de | G> i | O> colors:

a | G> + b | O>

on a i b són dos nombres reals. El seu significat és senzill: indiquen la probabilitat del color que tindrà la boleta en sortir de la caixa. És a dir, si una boleta es troba en estat 0,5 | G> + 0,5 | O>, en obrir-se la caixa la probabilitat de tenir | G> és del 50%. En la quàntica aquesta propietat de les boletes es diu propietat de la superposició. Això ens porta a una altra llei especial: les boletes dins de la caixa poden estar en estat de superposició, però quan obrim la caixa només poden ser | G> o | O>. No hi ha superposició fora de caixa. El sinònim quàntic d'obertura de caixa és el mesurament, on s'anul·la l'estat de solapament de les boletes (veure figura 1).

No obstant això, les caixes no s'utilitzen únicament per a guardar boletes. Si agita la caixa de manera diferent, podem canviar l'estat de la boleta, per exemple canviant les proporcions de les combinacions. L'equivalent a l'agitació són operacions quàntiques. Hi ha molts tipus i nosaltres no aprofundirem. De moment, pensa que agitant la caixa som capaces de realitzar les operacions que desitgem.

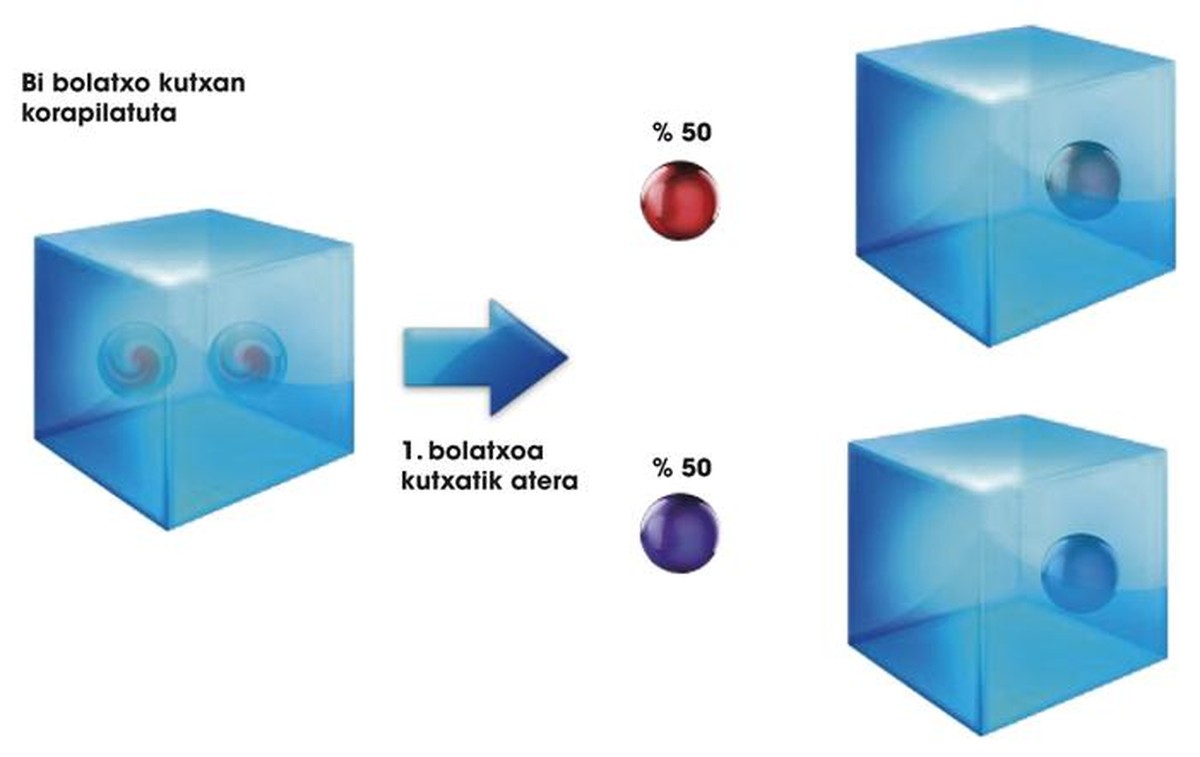
Per a acabar amb aquest apartat, hem d'esmentar una altra particularitat de les nostres caixes i boletes. Si col·loquem dues boletes en la mateixa caixa i agitem la caixa, podem coronar les boletes juntes. Així, agitant la Boleta 1 i la Boleta 2 en la mateixa caixa, podem obtenir l'estat 0,5 | G 1 G 2 > + 0,5 | O 1 O 2 >. En Quàntica, aquesta situació es diu complicada, ja que les dues boletes queden complicades. En aquesta situació, si de la caixa només sortim la boleta 1 i veiem que està en estat | G>, ja sabem que sense haver de sortir de la caixa, la boleta 2 estarà en estat | G> (veure figura 2). Tingues en compte que això no és possible si les dues boletes estan en dues caixes, encara que estiguin superposades. En aquest cas, si surt la primera boleta i | G>, la segona boleta pot ser | G> o | O>. No existeix cap relació entre tots dos.

Són molts els estudis que s'estan duent a terme sobre les dificultats. Després de complicar dues boletes es mantenen complicades fins que es realitza un mesurament, encara que la distància entre elles sigui molt gran. Sigui com sigui la distància, la mesura en una boleta actua bruscament sobre l'altra boleta i canvia el seu estat encara que no l'hàgim tocat. Encara no sabem per què i com es complica, però ja som capaços d'utilitzar-ho. Com es pot imaginar, és la clau per a aconseguir la teletransporte.

Figura . Principi de superposició i mesura en el cas d'una boleta. Ed. Gorka Azkune

Figura . El principi de l'embolic i les seves conseqüències amb dues boletes. Ed. Gorka Azkune

Telreporte quàntic

Tenim dos bons amics, Alaitz i Beñat, i un dia junts van decidir complicar dues boletes. Després de l'embolic, cadascun va agafar la seva boleta en una caixa especial, sense mirar mai a la boleta. Així, quan cadascun es traslladava a la seva casa, les dues boletes seguien embullades, malgrat estar allunyades.

Alaitz té una altra boleta a la seva casa, ficada en una altra caixa, en un estat de superposició desconegut. Alaitz, amant dels reptes, pensa: "Com puc enviar a Beñat la nova boleta en la situació en la qual es troba sense moure't de casa? ". No pot treure la boleta de la caixa, ja que en aquest cas canviaria el seu estat natural a | G> o | O>. Ell vol enviar la boleta a Beñat en el seu estat natural, això és, a | G> + b | O> en situació de superposició. Alaitzena sembla un repte difícil, no?

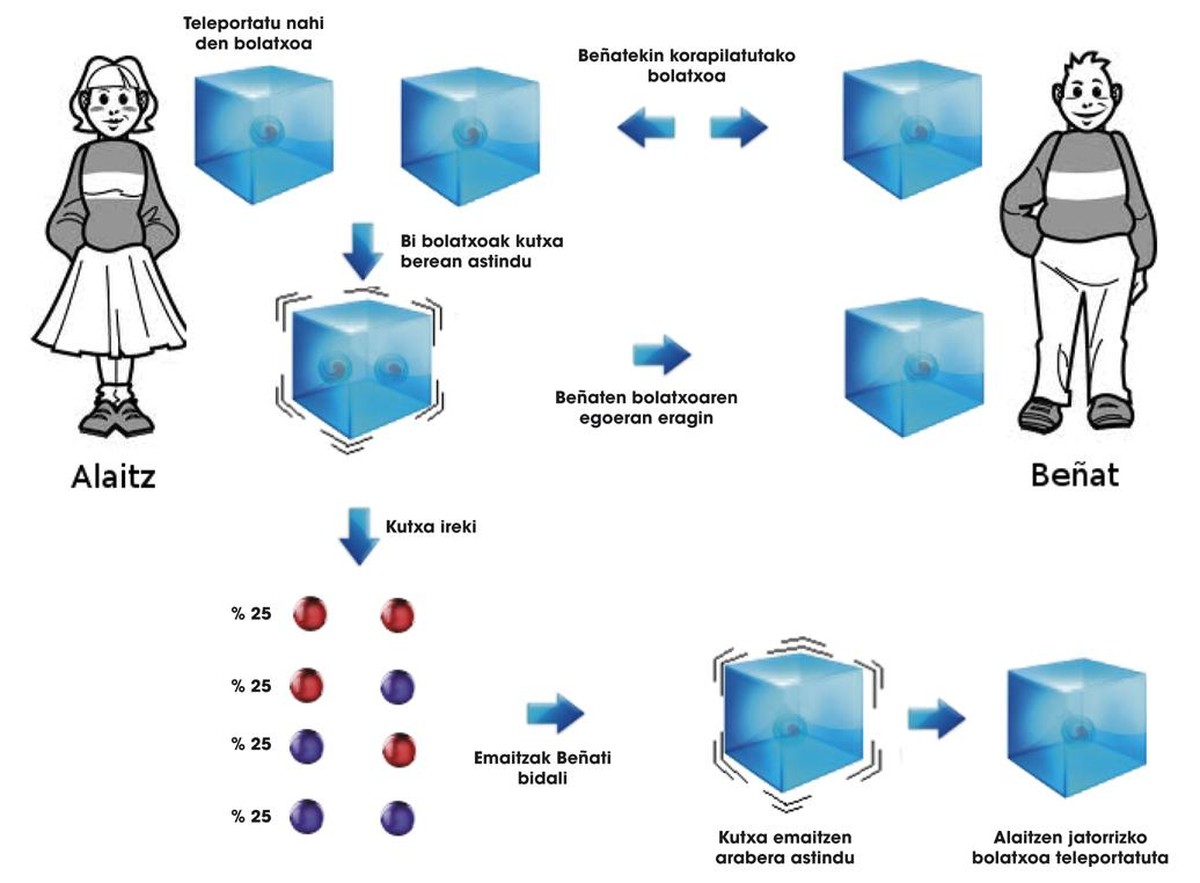
Però com Alaitz és una noia intel·ligent, troba una solució. La boleta que vol enviar a Beñat la col·loca en la mateixa caixa amb la qual ja tenia embullada amb Beñat. Recorda que Beñat té la seva boleta guardada a la seva casa. Alaitz realitza diverses operacions en les dues boletes que té a les seves mans, sacsejant la caixa d'una manera especial. Com a conseqüència de l'enredamiento, aquestes operacions també afecten la boleta de Beñat, i Alaitz sap a més la seva influència. Per això, obre la caixa per a conèixer l'estat de les seves dues boletes. Les boletes poden estar en estat | GG>, | GU>, | UG> o | UU> respectivament. Segons el resultat, Alaitz coneix l'estat de la boleta de Beñat. Sorprenentment, després de les operacions d'Alaitz, aquestes possibles situacions són a | G> + b | O>, a | O> + b | G>, a | G> - b | O> i a | O> - b | G>.

Així que Alaitz, tan aviat veu les seves dues boletes, li crida Beñat i li diu com agita la caixa de la seva boleta per a aconseguir la boleta que Alaitz vol enviar. Quàntica ens ha demostrat que, sabent com assotar la caixa, de les quatre situacions que hem presentat, es pot obtenir l'estat original de la boleta d'Alaitz. El procés descrit es pot veure en la figura 3. Al final del procés, la boleta d'inici d'Alaitz ha estat telaudida a casa de Beñat!

Figura . Procés de teletransporte d'una boleta entre Alaitz i Beñat. Ed. Gorka Azkune

És la teletransporte quàntica la teletransporte dels nostres somnis?

La resposta breu a aquesta pregunta és negativa. Segons la física actual, no es pot aconseguir alguna cosa semblança a la teletransporte de Star Trek. Per què? Quines diferències hi ha entre la teletransporte quàntica que acabem de veure i la de Star Trek?

1. Entre Alaitz i Beñat mai s'han mogut boletes: L'estat de la boleta inicial d'Alaitz s'ha copiat a la boleta de Beñat, però no hi ha hagut transport de matèria.

2. La teletransporte quàntic no és instantani. Perquè es produeixi el teletransporte, Alaitz ha d'informar a Beñat de la situació de les seves dues boletes per telèfon, correu electrònic o cridant. Aquesta comunicació pot produir-se a la velocitat màxima de la llum però no a la velocitat. Per tant, la telreporte quàntic necessita un temps per a dur-se a terme i no pot superar la velocitat de la llum.

Malgrat els problemes, sembla que, almenys teòricament, podem aconseguir que una persona pugui teletransportarse. Però tingues en compte les dificultats tècniques:

1. Per a portar una boleta de teletreball hem de tenir una altra en l'arribada (boleta de Beñat). Per tant, hem de tenir altres partícules en la meta de la persona que volem teletransportar.

2. Les operacions i mesures haurien de realitzar-se tenint en compte totes les propietats de les partícules d'una persona. En el cas de les boletes, només hem esmentat el color, però les partícules quàntiques tenen moltes propietats.

3. Hauríem d'enviar tota la informació d'aquests milions de mesures en destinació utilitzant els canals de comunicació habituals.

Això és només el principi. En Quàntica ja s'ha vist que és molt difícil mantenir el nus entre dues partícules, que han de ser aïllades del món. Per tant, encara que no es menyspreï del tot, podem considerar gairebé impossible que una persona pugui teletransportarse. A més, i passant a un àmbit més filosòfic, és la mateixa persona la que hem teletransportado així? En definitiva, hem copiat la informació d'una persona a altres partícules de matèria. Deixem la pregunta en l'aire.

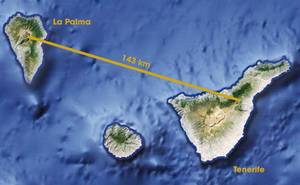
No obstant això, amb la tecnologia actual ja s'ha aconseguit teletransportar fotons i alguns àtoms. En el cas dels fotons, es va aconseguir la teladrinalización entre les illes de Tenerife i La Palma, imposant un rècord de 143 km (veure figura 4). Les explicacions d'aquest experiment van ser publicades en la prestigiosa revista Nature en 2012. Per part seva, investigadors de la Universitat de Maryland van aconseguir en 2009 teletransportar un àtom a una curta distància.

Teletransporte avui i demà

Figura . Experiment de teletransporte a les illes Canàries. Ed. Google earth

Dominem la teletransporte quàntic a nivell teòric: es coneixen les propietats d'aquesta, sabem com fer-ho i sabem les seves limitacions. Tecnològicament també s'han fet passos molt importants, tal com hem explicat. Estem convençuts que en el futur serem capaços de teletransportar distàncies més llargues i majors quantitats d'informació, però on està el límit? Qui sap.

La telreporte quàntic serà una tecnologia molt important en el futur. Imprescindible en la criptografia quàntica, serà una de les claus en el futur per a l'obtenció d'ordinadors quàntics. Segurament s'utilitzarà en aplicacions que ara no podem imaginar, que en principi només existia en l'àmbit de la ficció.

A Euskal Herria tenim l'honor de ser un grup d'investigadors capdavanters en aquests temes. El grup Quàntum Technologies for Information Science1, del Dr. Enrique Solano, que va venir de la mà d'Ikerbasque a Leioa, ja gaudeix de gran prestigi internacional. Exemple d'això és l'article publicat en la revista Nature en 2010.

Aquí i allà, els investigadors ens aportaran un nou coneixement sobre el nostre fascinant món. La telreporte quàntic ens obre noves portes, però ningú pot saber què estarà darrere d'elles. Com diu Pedro Miguel Etxenike, el nou coneixement augmenta el desconeixement, ja que cada resposta planteja mil noves preguntes.

Gorka Azkune Galparsoro

Ed. © Iñigo Ibáñez

(Azpeitia, 1982). Va estudiar Enginyeria Informàtica en la UPV. El projecte fi de carrera va ser realitzat en l'Institut Max Planck d'Òptica Quàntica, sota la direcció d'Ignacio Cirac. Ha treballat en Tecnalia en el camp de la robòtica i la intel·ligència artificial, i en l'actualitat treballa com a investigador a Deusto Tech per a aprofundir en la recerca en el camp dels sistemes intel·ligents amb l'objectiu de realitzar una tesi doctoral.

Bibliografia