Sota relativitat especial

1991/09/01 Martin Axpe, Iñaki Iturria: Elhuyar aldizkaria

• Fisika

Elhuyar. Ciència i Tècnica

En dos articles anteriors al , abordem escales de temps i mesures mundials comparant-les amb el quotidià. En aquesta ocasió abordarem la Teoria de la Relativitat Especial.

Encara així, a pesar que van transcórrer 86 anys des que es va conèixer per primera vegada aquesta teoria, sovint se'l considera una cosa oculta, incomprensible i sasimágico. Tots sabem qui va ser Einstein: el savi que va posar la ciència potes enlaire, el científic solitari i genial que sabia molt més que ningú, i molts més tòpics. Així mitificamos Einstein, situant-nos sobre un pedestal, el convertim en inaccessible i deixem la seva teoria per a alguns experts. Però podem fer alguna cosa més a conèixer-ho. En definitiva, si creiem que els habitants del pol sud no es mouen de memòria, per què no creure el que ens diu la Relativitat Especial?

En una simple articulació no obrim els ulls davant la nova veritat, clar, perquè per a això cal aprendre amb molt d'esforç, però podem acostar-nos a les conclusions.

Per tant, no mostrarem cap demostració. Assumint el que diu la teoria i les conseqüències que d'ella es deriven, canviarem d'escala perquè la seva essència influeixi en la nostra vida quotidiana.

Teoria de la relativitat especial

La Teoria de la Relativitat d'Einstein consta de dos apartats: el primer és la Teoria de la Relativitat Especial (que es representarà amb l'abreviatura TUE), en la qual s'analitzen els objectes de velocitat constant i el segon, la Teoria de la Relativitat General (TGV), que es tractarà en un article posterior.

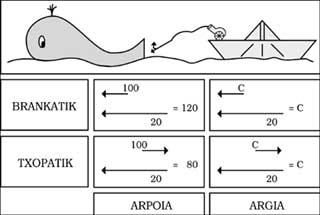
Pensem que estem en la talaia d'un poble de la nostra costa, explorant la mar oberta, i que veiem un vaixell que navega a 20 km/h. En un moment donat, el ballenero projecta l'arpó de proa a 100 km/h. Nosaltres, per tant, veurem sortir l'arpó a 120 km/h. Per contra, si en igualtat de condicions l'arpó és llançat des de la chopa, el veurem des de la nostra talaia a una velocitat de 80 km/h. Atès que els moviments del vaixell i arpó són de sentit contrari, les seves velocitats tendeixen a eliminar-se entre si.

Fins aquí no hi ha cap obstacle, però ara posarem un focus de llum en el lloc del canó arpó. Com la velocitat de la llum és de 300.000 km/s (s'indica amb el símbol c), segons el mateix raonament superior, nosaltres hauríem de veure els raigs de llum des de la nostra talaia a una velocitat de c+ 20 i c-20. El que passa no és això. De fet, veurem els raigs que provenen tant de la proa com de la chopa a la mateixa velocitat ( c). És més, independentment del moviment del focus de llum, la velocitat de la llum es mantindrà indefinidament (veure figura 1).

L'experiència ens ensenya aquest curiós comportament que s'oposa a la lògica. I que la màxima velocitat possible és la de la llum, és a dir, que la velocitat c no es pot superar. Per tant, el concepte (suma o resta de velocitats) aplicable en condicions concretes no és aplicable en condicions diferents. Això significa que a vegades les fórmules (lleis) aplicables no poden aplicar-se en altres ocasions? Einstein va respondre que no i va formular la TUE de la següent manera:

1. En totes les condicions són aplicables les mateixes lleis.
2. La velocitat de la llum sempre és constant (en buit) i mai es pot superar.

Per a completar el postulat anterior cal fugir de les velles fórmules de sempre i utilitzar les noves que va inventar Lorentz (veure figura 2).

No obstant això, aquestes noves fórmules porten amb si una sèrie de conseqüències més habituals.

Conclusions

Sense adonar-nos, en comprendre i explicar el món que veiem, pensem que hi ha velocitats infinites. Per exemple, ho he vist quan ha succeït, però per a això la velocitat de la vista hauria de ser infinita, o bé trigarà un temps a recórrer l'espai des del lloc on ha ocorregut fins als meus ulls. No obstant això, sabem que la velocitat màxima és c, per la qual cosa no hi ha velocitats infinites. D'aquí podem treure la primera conclusió: hi ha qui opina que els successos que ocorren simultàniament no són simultanis.

Per exemple, en el centre del vaixell hi ha un pescador i com els raigs que van per la proa i la chopa han de recórrer la mateixa distància, els veurà al mateix temps. Però des de la nostra talaia veurem que perquè el raig brancótico arribi fins a la meitat del vaixell ha de recórrer un camí més curt que el chopático (veure figura 3). Per tant, el brancánico arriba abans i no els veiem alhora!

Seguint un raonament similar, veurem els objectes que es mouen respecte a nosaltres més curts que quan estan parats, i com més gran sigui la velocitat, més curt serà l'objecte.

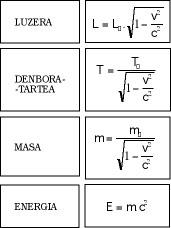
La tercera conclusió es refereix al temps i és bastant popular. Segons això, en els cossos en moviment el temps passa més a poc a poc. Encara que sembli que no hi ha justificació per a això, és una conseqüència directa de les noves fórmules. Finalment, cal esmentar que la massa en repòs dels cossos és més lleugera que quan es mouen i que l'energia i la massa són el mateix. L'aspecte matemàtic de tot això es reflecteix en la figura 4.

A pesar que aquestes estranyes conseqüències poden ser motivades per la teoria, algú podia pensar que en la vida quotidiana mai s'ha vist aquest efecte. La veritat és que s'han vist. Perquè els veuen tots els dies... els que miren les fraccions bàsiques. La raó d'això radica en la velocitat: aquests efectes només es produeixen quan es troba prop de la màxima velocitat en joc (començant pels electrons i altres fraccions), i com les velocitats que sofrim i veiem en la nostra vida estan tan lluny del màxim, no percebem gens especial.

No et desesperis. Perquè la TUE sigui una mica més pròxima, més domèstica i més comprensible, us proposo un joc: canviarem la velocitat c.

Un dia en carreres

Pensem que la velocitat de la llum és de c = 30 km/h. Amb aquesta condició els efectes del TUE serien evidents en la nostra vida. Per a començar, mai podríem superar els 30 km/h independentment del recurs. I quines altres diferències observaríem llavors?

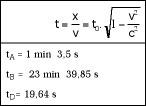
Suposem que és diumenge i hem anat a carreres de cotxes. Ens hem assegut en la graderia per a veure la carrera des d'allí, però encara falten uns minuts, per la qual cosa analitzarem les característiques de cada detall. Veiem que la pista és una recta de 2 km de longitud. Així mateix, en la sortida hi ha tres cotxes preparats de 3 m de longitud (veure figura 5). Finalment s'ha iniciat la carrera amb els cotxes A i D bastant igualats (29 i 29,9 km/h respectivament), però el B s'ha llançat per avaria o el que és impossible (5 km/h).

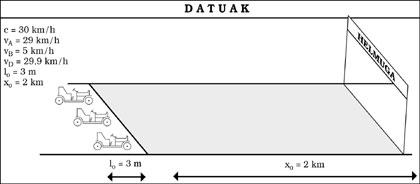
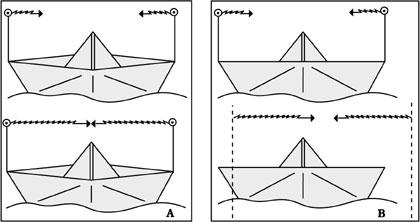
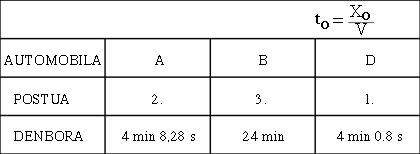
En passar per davant de nosaltres, aquests cotxes de 3 m de longitud parats veurem més curts i, en concret, com més ràpid anem, més curts ens semblaran (veure figura 6). No obstant això, una vegada acabada la carrera, comprovem que les tres d'elles tenen una longitud de 3 m. Mentrestant, el guanyador serà D, per descomptat, els temps oficials en meta seran els de la figura 7.

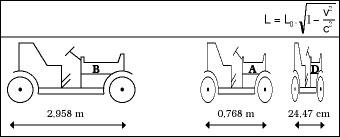
Si preguntem als pilots, rebríem una imatge bastant diferent. I és que encara que el criteri del conductor B coincidís més o menys amb el nostre, les opinions d'i D serien diferents. Per a A, per exemple, la pista seria de 512 m i defensaria que D tenia 163 m (veure figura 8).

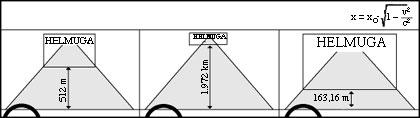
El mateix passaria amb els temps. Creiem que mentre la distància entre A i D és de 7,5 segons, consideren que ha estat major. I és que nosaltres hem trigat 4 minuts a anar de la sortida D a l'arribada, però ella només ha trigat 19 segons a fer el mateix (veure figura 9). Per tant, és més jove que si s'hagués detingut en la graderia per la velocitat. Això és estalviar temps!

La paradoxa dels bessons

Però aquí sorgeix una preocupació. Com més lleuger vagi el cotxe, més curt l'hem vist i, simètricament, els pilots han vist els objectes de la pista com més ràpid és anar. En això consisteix precisament la relativitat, és a dir, un pensa que l'altre és més curt, però l'altre creu que el primer és més curt, i ni un ni l'altre té raó, o tots dos tenen, perquè les coses no tenen l'únic aspecte real, sinó que depenent del moviment de l'observador adoptaran diferents formes.

I ara ve la inquietud que he esmentat: nosaltres hem vist als pilots una mica més joves, però ells a nosaltres més antics i no més joves com ho faria la simetria de la relativitat. En el cas del temps no es compleix la relativitat? Aquest nus es coneix com la paradoxa dels bessons. La resposta és favorable al TUE. Vegem per què.

Inicialment es va comentar que és aplicable en aquells casos en els quals no existeix acceleració TEE (velocitat constant). Si la pista està parada, podem considerar que els cotxes es mouen o que els cotxes es mouen quan estan parats, i tant un com l'altre estan rectes. Així que nosaltres veurem que el temps va més a poc a poc en els cotxes, i els pilots veuran que el temps va més a poc a poc en la pista mentre la velocitat dels automòbils roman constant. Aquí es compleix la simetria de la relativitat. No obstant això, els automòbils han de sofrir una acceleració en el moment del seu moviment i un frenat final per a detenir-se.

En aquests dos moments especials la simetria es trenca i no podem dir que el que es mou (pista o cotxe) sigui el mateix. Atès que un d'ells (el cotxe) té un moviment especial, el pilot sap que no està parat. La conseqüència és que els pilots i els de pista estiguin d'acord per a respondre a la pregunta d'on està el temps més lent.

Boig en el món

I quin més passaria en un món tan baix?

A les 8’30 del matí Jone i Mikel han sortit de casa perquè tenen un examen en l'Institut de Bilbao. Tots dos deixen una assignatura per a aprendre en el camí. Jone viu a Deusto. Per tant, ha sortit a peu i ha arribat en aproximadament mitja hora, havent acabat l'assignatura. Mikel, per part seva, en residir a Barakaldo, ha agafat a les 8,30 el Tren d'Alta Velocitat (29,9 km/h) i ha arribat a les 9, però no ha tingut temps de llegir el començament de l'assignatura, ja que a penes han passat uns segons en la seva vida interna.

I per les mateixes raons, els astronautes tindrien una vida molt dura. Suposem que els espais poden circular a una velocitat de 29,999 km/h. En aquest cas, el viatge d'anada i volta a la Lluna passaria tres anys en la Terra, mentre passarien dues setmanes en la vida de l'astronauta (inclosa l'estada en la superfície de la Lluna). Després de quinze viatges al llarg de la seva vida, l'astronauta comprovaria que la seva dona i els seus fills fossin els seus majors.

I de tot això, al final què?

Dit això, el TUE no tindrà cap incidència ni als trens ni en la nostra manera de vida normal. A més, els efectes descrits no han de prendre's literalment, sinó com una aproximació. De fet, els dies i els anys serien molt diferents si hi hagués c = 30 km/h. El que veus no és un autèntic resum de coses, sinó una espècie de gir i deformació. Com més gran sigui la velocitat d'un objecte, més vermellós apareixeria, etc. Però tots aquests detalls ens continuen igual (els curiosos poden acudir al quadre de Crítica de la idea resumeixen).

La idea que hem de retenir és que en la naturalesa hi ha una velocitat màxima, la de la llum, la qual cosa produeix uns efectes estranys o anormals quan ens acostem a aquesta velocitat. I per part meva voldria afegir la següent idea: Encara que les petjades del TUE són increïbles, són perfectament comprensibles. El realment sorprenent és que la teoria d'Einstein només depèn d'uns pocs científics. Arrelament! No som capaços de dissenyar el motor d'automòbil, però entenem les bases de funcionament. Així sigui també amb el TUE!

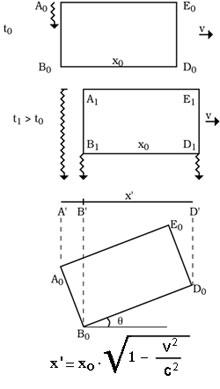
CRÍTICA IDEA RESUM Per aquest motiu no podem veure el resum. Suposem un cos A 0 B 0 D 0 E 0 que es mou amb velocitat v. Nosaltres estem alineats amb la direcció del moviment, estant la B 0 D 0 més a prop. Com sabem, la qual cosa sabem en un moment determinat són els raigs que arriben simultàniament en aquest moment. Així, com es pot apreciar en la figura, els raigs que parteixen de 0 a B 1 i D 1 arribaran als nostres ulls simultàniament. El que veurem, per tant, tal com hem explicat en l'article, no és només un resum B’D’, sinó també una imatge oculta de 0 B 0 costat A’B’. Però aquesta forma de ‘A’B’D’ que veiem i el cos amb l'angle q serien iguals a la imatge girada, com es veu en la imatge. Per tant, quan v està prop de c veiem que les coses giren i, al mateix temps, el que hi ha darrere de les coses és espectacular.