Comment opérer ? (I). Addition et soustraction

1990/10/01 Angulo, Patxi Iturria: Elhuyar aldizkaria

• Matematika

Dans les numéros précédents, nous avons plongé dans l'histoire des chiffres. Là, nous avons vu les systèmes utilisés par l'homme. Ce qui a motivé à inventer les chiffres a été la nécessité de compter (et aussi les opérations liées au calcul). Mais, jusqu'à ce que notre système apparaissait, comment les opérations sont-elles résolues? Cet article traite de cette question. Les traces trouvées nous permettent de nous approcher de la façon dont l'homme a calculé.

Ce qui l'a amené à inventer les chiffres, comme cela a été dit, était la nécessité de compter. Le comptage était fait avec le corps. Bien que dans certains cas on utilisait en plus de la main d'autres parties du corps (pieds, bras, visage, ...), on peut dire que la première calculatrice humaine était la main. La main, probablement, a créé les bases dix, cinq, douze et vingt. En plus de compter manuellement, l'homme effectuait des opérations. À cette époque, nous devons nous rappeler que l'être humain ne comprenait ni ne connaissait aucun numéro écrit. Cependant, il a pu effectuer plusieurs multiplications.

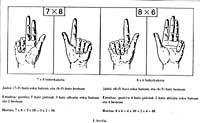
Par exemple, pour multiplier deux nombres entre 5 et 10, dans une main ils baissaient autant de doigts qu'un produit et la différence entre 5, dans l'autre le produit et le 5. Le résultat était obtenu en multipliant le nombre de doigts abaissés sur les deux mains par dix (de la tête) et en s'ajoutant au produit du nombre de doigts sans baisser sur les deux mains (figure 1).

Ceci a sa vérification mathématique: si x et y sont des nombres compris entre 5 et 10, dans une main (x-5) descendent les doigts (y-5) et dans l'autre (y-5) et sans descendre, dans la première il y a 5 - (x-5) et dans la seconde il y a 5 - (y-5), le nombre de doigts étant descendus (x-5) + (y-5). Réalisation des opérations mentionnées 10 [(x-5) + (y-5)] + [5 - (x-5)] . [5 - (y-5)] = 10 (x+y-10) + (10-x) . Nous avons (10-y) = 10x + 10y - 100 + 100 - 10x - 10y + xy = xy.

Une règle similaire servait à multiplier deux nombres entre 10 et 15 ou deux nombres entre 15 et 20, etc.

Pour multiplier deux nombres entre 10 et 15, dans chaque main se pliaient autant de doigts qu'un produit et la différence entre 10 ; on multipliait par 10 le nombre de doigts accrus ; puis on multipliait les doigts qui étaient descendus dans deux mains et finalement on ajoutait les deux résultats et 100.

Tous ces draps ont leur vérification mathématique, bien que l'homme ne comprenne pas alors.

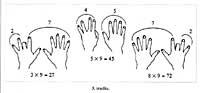
À titre de curiosité, nous indiquerons manuellement le tableau de multiplication du nombre 9. En ouvrant les deux mains devant nous, de gauche à droite, après avoir donné aux doigts les valeurs 1, 2, 3, ..., nous pencherons le doigt correspondant au nombre indiquant l'autre produit qui a comme produit 9 et nous donnera le résultat le nombre de doigts restant de chaque côté de ce doigt; le côté gauche le décimal et le côté droit l'unité (figure 3).

Mais voyons maintenant les premières opérations écrites. Avant de commencer, nous préciserons que nous n'utiliserons pas les chiffres actuels.

Addition: Addition

C'est certainement l'opération la plus simple, tant théorique que pratique. Nous verrons quelques exemples tout au long de l'histoire de cette opération.

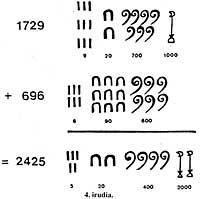
Pour les Egypti ajouter deux numéros, comme 1729 et 696, en écrivant sur la chanson

(Figure 4). Ensuite, ils recueillaient les mêmes symboles et ils ont obtenu le résultat de remplacer 10 symboles d'un ordre par un ordre suivant.

Un autre exemple vient de la main de l'abaque. Dans l'abaque, pour joindre deux numéros étaient écrits les deux par des chants, après le baptême, et le résultat apparaissait après avoir fait les résumés nécessaires. Un abaque spécial, réalisé dans le sable par des colonnes, a été utilisé par les hindous qui étaient habiles dans le calcul. Dans chaque colonne ils écrivaient un nombre, laissant la colonne vide pour indiquer zéro ou désordre. La somme se faisait comme l'autre abaque, mais en remplaçant les chants par les nombres. De là vient l'algorithme que nous utilisons maintenant.

Cependant, les hindous avaient un autre algorithme, le soi-disant recul. Ceci (les nombres qui étaient groupés par colonnes commençant par la gauche) consistait à effacer la portée quand étaient les k (figure 5).

XVI. En 1540, Gemma Frisius a créé un algorithme. Il écrivait les nombres de majeur à mineur et de haut en bas et joignait les numéros de chaque colonne. Les résultats partiels ainsi obtenus étaient écrits de droite à gauche et recueillis (Figure 6).

Comme vous pouvez le constater, la plus grande différence entre les différents algorithmes était dans l'expression des résultats.

Soustraction de la soustraction

Ce qui rend cette opération intéressante est le cas dans lequel le resteur est plus grand que la minuendo, mais nous n'allons pas y entrer. L'algorithme de soustraction n'était pas standardisé. Il existe de nombreuses méthodes pour effectuer cette opération. Cependant, l'idée de la demande de formation est ancienne et étendue. La méthode, ou idée, a été utilisé par Fibonacci (Léonard de Pise) en 1202.

Cependant, nous allons apporter l'algorithme de Columbia qui évite de demander la préparation. Dans l'exemple suivant, on peut calculer la différence 8432-5976 selon l'algorithme de Columbia: