Equacions diferencials a la recerca d'estabilitat

2009/11/01 Alberdi Celaya, Elisabete - Matematikan lizentziatua eta doktoregaia Iturria: Elhuyar aldizkaria

• Matematika

També en matemàtiques hi ha disciplines en les quals l'estabilitat és fonamental. Els que volem fixar-nos tenen cabuda en els programes de les carreres científiques i tècniques, s'utilitzen en la formulació de models matemàtics i per a alguns es busca un resultat analític, mentre que uns altres es resolen amb mètodes numèrics --aproximacions - i amb l'ordinador com a acompanyant. A alguns alumnes els agrada, però a la majoria els causen maldecaps. Què són? Són equacions diferencials. Les equacions diferencials, igual que l'ésser humà en la vida, busquen el major camp d'estabilitat possible.

Utilitat de les equacions diferencials

Un model matemàtic és un dispositiu que descriu un sistema o succés de la vida. La formulació d'un model matemàtic comença amb la identificació de les variables que influeixen en el sistema, és a dir, produeixen un canvi en el sistema. A continuació s'estableixen hipòtesis raonables sobre el sistema, identificant les lleis empíriques aplicables. Algunes d'aquestes hipòtesis indiquen la mesura de la variació d'algunes de les variables prèviament definides. L'enunciat matemàtic d'aquestes hipòtesis serà una equació o un sistema d'equacions en el qual apareguin les derivades, que és el sistema d'equacions diferencials.

La seva resolució concreta ens permetrà conèixer el comportament del sistema. Però, de què parlem quan parlem de model o model matemàtic?

En la cinètica de les reaccions químiques interessa la seva evolució al llarg del temps. A l'ésser les velocitats derivades del temps de qualsevol variable, la cinètica de les reaccions es modeliza mitjançant equacions diferencials. Exemple d'això és el cas que totes dues substàncies generen un tercer. Les variables són concentracions de substàncies, mentre que les lleis empíriques són la llei d'acció de masses i la llei de conservació de masses. La primera ens diu que el producte de les concentracions dels reactius és proporcional al producte de les concentracions dels productes, i les segones, la suma de les masses dels reactius és igual a la dels productes.

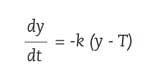
En la refrigeració dels cossos també s'utilitzen equacions diferencials. Per exemple, si traiem un pastís del forn a 150 °C i volem saber la seva temperatura en qualsevol moment. Si estem investigant l'homicidi o l'assassinat d'una persona i volem calcular a quina hora va morir, utilitzarem la llei de refrigeració de Newton. Aquesta llei estableix que el canvi de temperatura de la superfície corporal és proporcional a la diferència entre la temperatura corporal i la temperatura ambient. Així, si la temperatura del cos en l'instant t és i ( t ) i la temperatura en el mitjà T, segons la llei de Newton, es complirà la següent equació diferencial:

sent k 0 la proporcionalitat constant.

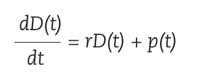
Volem calcular els interessos que ens donarà una quantitat de diners que ingressem en el banc? Haurem d'utilitzar equacions diferencials. Suposem que introduïm en el banc la quantitat D 0 i ens paguen un tipus d'interès r. Direm D ( t ) a la quantitat que tindrem dins de t anys. La variació de la quantitat serà la suma de la variació per acumulació d'interessos i la variació d'ingressos que realitzem en el banc, p de fórmula.

Hi ha, per tant, que modelar en la vida quotidiana utilitzant equacions diferencials.

Dificultats de resolució

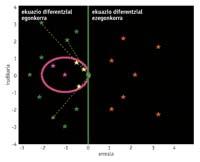
Una vegada obtinguda l'equació diferencial s'ha de resoldre. A vegades, no és possible el seu alliberament analític, i mitjançant mètodes numèrics s'obté un resultat aproximat. Les equacions diferencials inclouen uns autovalores complexos que denominarem l. Quan la part real d'aquests autovalores és positiva, l'equació diferencial és inestable i el resultat aproximat que obtindríem utilitzant un mètode numèric per al seu alliberament no té per què semblar-se a la solució real, ja que un petit canvi té un fort impacte en ells. Per això, els mètodes numèrics s'apliquen a equacions diferencials estables, autobalioides de part real negativa. D'altra banda, el propi mètode també té una zona d'estabilitat. I si es vol aconseguir un bon resultat, els autovalores han de situar-se allí. Per tant, els autovalores de les equacions diferencials estables no presents en aquesta zona es traslladen a la zona d'estabilitat, multiplicant els autovalores per un número h mesurat (0,1) que denominarem mesura del pas.

La mesura del pas és fonamental per a resoldre l'equació i, per descomptat, no pot ser qualsevol número. En termes de fiabilitat, el mètode de resolució ha de ser prou petit com per a mantenir-se dins de la zona d'estabilitat i prou gran com per a donar el menor nombre de passos possibles de cara al treball. Com aconseguir aquest equilibri?

Equilibri de l'àrea d'estabilitat

Per a saber quins passos es poden donar en el mètode numèric cal fixar-se en l'error. En utilitzar mètodes numèrics es genera un error local en cada pas. Però hi ha un altre error que apareix en la longitud, que és la reproducció dels errors de cada pas, i que està format per les potències d'un número anomenat factor d'amplificació. Per a evitar l'augment de l'error, el factor d'amplificació ha de ser menor que la unitat. La zona que compleix aquesta condició és la coneguda com a zona d'estabilitat del mètode. Doncs bé, l'autovalor l ha d'estar en la zona d'estabilitat després de multiplicar-se per h perquè el factor d'amplificació sigui menor que la unitat. Però no sols això, una vegada que el producte l .h es troba en la zona d'estabilitat, es veu si el número h ha de ser menor, ja que qualsevol número que sigui menor que h que hem trobat fa possible que després de multiplicar l'autovalor s'emporti a la zona. Dels números que permeten portar l'autovalor al camp, el número h que manté l'error local dins d'una tolerància és el que es tria com a mesura del pas. Aquesta mesura de pas permet tenir controlats els dos errors (local i longitudinal). Com més gran sigui aquest número, major serà el nombre de passos que podrem donar i més ràpid serà el resultat, un objectiu que el gran camp d'estabilitat permet aconseguir.

Però la mesura de la zona d'estabilitat també està condicionada. Depèn de l'ordre. L'ordre és el paràmetre que s'utilitza per a mesurar la precisió del mètode i és més precís com més alt és l'ordre. Normalment, a mesura que augmenta l'ordre, la zona d'estabilitat disminueix. Això ens obliga a fer passos menors, encara que el resultat sigui més precís.

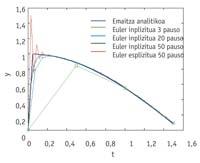
El propi mètode també condiciona la mesura de la zona d'estabilitat. Els mètodes implícits solen tenir una àrea d'estabilitat major que els explícits, però també presenten desavantatges: la principal és que es requereixen operacions més o menys complexes que en els mètodes explícits. Per això, quan els autovalores no són molt grans, es prefereix el mètode explícit, ja que les operacions a realitzar seran més sostenibles.

El somni seria trobar la màxima estabilitat en ordres alts i mètodes explícits, però tampoc en aquest camp de la ciència hi ha raresa. Amb la finalitat d'aconseguir que les equacions diferencials es deixin anar fàcilment per mètodes numèrics, són nombrosos els treballs realitzats per a augmentar el camp d'estabilitat. Els primers són els mètodes d'Adams Bashforth i Moulton, en els quals s'utilitza tant la informació de l'últim pas com la informació d'altres passos més ràpids per a construir el següent pas. D'aquesta forma es va aconseguir pujar l'ordre del mètode numèric, i el d'ordre 1 té un camp major que el d'Euler explícit (també d'ordre 1). Una de les propostes més importants va ser la denominada BDF (fórmula backward differentiation) realitzada per Gear cap a 1971, un mètode implícit que utilitzava informació en diversos passos més lleugers. El mètode BDF va aconseguir que les zones d'estabilitat fossin també importants en ordres elevats. Últimament predominen els mètodes que utilitzen la derivada 2 o els anomenats punts de superfuturo, ja que tenen grans àrees d'estabilitat, encara que incrementen el treball a realitzar en cada pas.

Molts petits passos o pocs grans passos, aquí està la clau. En aquesta competència, la primera opció, amb molts petits passos, té l'avantatge de la fiabilitat i la segona l'optimització del treball. Unificar totes dues opcions en una sola ocasió seria excel·lent, ja que s'aconseguiria "fiabilitat sense treball excessiu". La clau per a trencar aquest equilibri radica en mètodes de gran camp d'estabilitat, que no posen límits tan rígids a la mesura del pas. Per això és possible fer passos no tan fiables i grans passos fiables.