Vacas d'Arquimedes

1994/02/01 Angulo, Patxi Iturria: Elhuyar aldizkaria

• Matematika

Però la seva afició no es referia a problemes matemàtics profunds. Per contra, Arquimedes també va abordar l'aspecte LÚDIC de les matemàtiques. Un exemple d'això és el problema de les vaques.

La matemàtica clàssica ens va deixar problemes de difícil resolució (quadratura del cercle, trisecció de l'angle, teoremes de Fermat, ...). Amb noves idees o raonaments enginyosos s'han resolt moltes d'elles o s'ha demostrat que són insolubles. Uns altres, no obstant això, continuen esperant resposta. És sorprenent que entre tants problemes, els problemes d'Arquimedes només necessitin càlculs. Per a poder fer aquests càlculs han hagut de passar 2000 anys. Eren càlculs tan pesats que només l'ordinador podia resistir.

a. C. III. Estem en el segle XX, Arquimedes ha donat una aproximació al número:

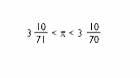
La Clau Apolonio, a més d'oferir una millor aproximació, ha criticat el treball d'Arquimedes en el tractat sobre la multiplicació de grans números. Arquimedes, atabalat per fets anteriors, prepara una venjança en inventar i enviar un difícil problema que necessita grans números, dels quals domina als seus competidors. Es desconeix la resposta d'Apolonio, però també ha enviat el problema a Eratòstenes, el bibliotecari d'Alexandria, i gràcies a això ha arribat a les nostres mans.
Tot això és llegenda i no sabem si és cert o no. D'altra banda, el problema és, almenys, el de C. II. També s'admet que és un subordinat i que els números a utilitzar per a resoldre són veritablement grans. La solució més petita, per exemple, té 206.545 xifres.

L'enunciat complet del problema va ser descobert en 1773 per Gotthold Ephraim Lessing en una biblioteca de Wolfenbüttel. Estava escrit en grec i estava format per línies apariades. La resumida pot quedar com segueix:

Calcula, amic, el nombre de caps de bestiar solars. Pensa en això si tens coneixements. Calcula una vegada el nombre de persones que s'allotjaven en les planes sicilianes, dividides per colors en quatre grups: un blanc, un altre negre, un altre vermell i l'últim pinto. Els toros eren més que vaques, en les següents condicions:

1. Toros blancs = toros vermells + (1/2 + 1/3) toros negres.
2. Toros negres = toros vermells + (1/4 + 1/5) toros pintats.
3. Toros pintos = toros vermells + (1/6 + 1/7) toros blancs.
4t Vacas blanques = (1/3 + 1/4) saldo negre.
5. Vaques negres = (1/4 + 1/5) saldo pintat.
6è Vacas pintes = (1/5 + 1/6) saldo vermell.
7. Vaques vermelles = (1/6 + 1/7) saldo blanc.

Si pots donar el nombre de caps de bestiar i vaques per cada saldo, amic, no tens rival entre els números. Però encara no pots formar part del grup de savis. Per a això haurà de tenir en compte les següents relacions entre els caps de bestiar solars:

8è. Toros blancs + toros negres = tot el quadrat (p2).
9. Toros pintos + toros vermells = número triangular (n(n+1)/2).

Quan calculis tot el saldo, llavors, amic, apunta't de ple dret i presumeix que el teu nom brilla en el món del coneixement.

Com es pot observar, dos problemes apareixen en un. Les set primeres condicions són fàcils de resoldre. No obstant això, els nou han creat dificultats durant 2.000 anys.

Cal tenir en compte que tots dos accepten infinites solucions. El problema consisteix a buscar la solució més petita. La realització d'operacions algebraiques permetrà obtenir els següents resultats:

Toros blancs = 10 366 482 K Toros negres
= 7 460 514 K Toros pintos
= 7 358 060 K Toros vermells
= 4 149 387 K Vacas blanques

= 7 206 360 K Vacas negres
= 4 893 246 K Vacas pintes
= 3 515 820 K Vacas vermelles
= 5 439 213 K

En els resultats anteriors K és qualsevol nombre natural. Donant valors a K s'obtenen diferents solucions. La solució més petita s'obté fent K = 1. En aquest cas el nombre total d'animals és de 50 389 082.

Quant al segon problema, sembla que en l'època d'Arquimedes no hi havia eines per a resoldre. I és que fins fa 100 anys no es va aconseguir cap avanç. En 1880 A. L'alemany Amthor va fer més útils les equacions i va dir que la solució començava per 776 ... i tenia 206.542 xifres. Va encertar en la primera, però en la segona s'equivocava de 3 xifres.

La primera solució sense errors es va obtenir en 1965 mitjançant un ordinador, però no es va publicar en cap lloc. Autors del programa H.C. Willians, S. a. German i C.R. Es tracta dels zarnques canadencs. En 1981 Harry L. El nord-americà Nelson va utilitzar el problema per a provar l'ordinador CRAY-1. Va obtenir la solució en 10 minuts i la va imprimir en 47 pàgines. Les 47 pàgines es troben en el número 3 del volum 13 de la revista “Journal of Recreational Mathematics”.

Per què les solucions del primer i segon problema són tan diferents? Complir la condició 8 no és tan difícil. Els toros blancs i negres sumen 17 826 996 K. Per tant, prenent K = 17 826 996, obtenim el quadrat complet. La dificultat sorgeix quan es té en compte la condició 9.

La condició 8 pot escriure's com:

p ² = 17 826 996 K
= 4 . 4 456 749 K;

ara, triant K = 4 456 749 t ² i substituint-ho en la igualtat anterior, s'obté:

p ² = 4 . 4 456 749 4 456 749 t ²
= ² . (4 456 749)2 . t ²
= (2 . 4 456 749 t) ² ,

és a dir, tenim tot el quadrat. Aquest és el progrés que va aconseguir Amthon. Així, si se selecciona K = 4 456 749 t2, la condició 9 es pot escriure com:

Toros pintos + toros vermells = 51 285 802 909 803 . tenint en compte que t ²

51 285 802 909 803 t ² = n (n+1) / 2

n, sent t nombres naturals.

(Recomanem al lector que no busqui la solució de la igualtat anterior).

Els que van utilitzar el problema d'Arquimedes per a provar el CRAY-1 no es van quedar a gust amb la primera solució i van començar a buscar les cinc següents. La major d'aquestes cinc xifres supera el milió d'euros. Bon saldo!

La nostra pregunta és com es podia viure tant de bestiar a Sicília?