Serions-nous capables de combattre une épidémie de zombies ?
2013/04/01 Alberdi Celaya, Elisabete - Matematikan lizentziatua eta doktoregaia Iturria: Elhuyar aldizkaria

The Walking Dead
Plusieurs histoires de science-fiction racontent l'apocalypse de zombies. Dans ces cas, après la mort de l'homme, il se ressuscite et devient zombie. Dans la plupart des cas, ces êtres ressuscités, les zombies, sont humains ou cannibales. Ils sont maladroit, avec le regard moyen perdu, avec les mains en avant marchant et se déplacent maladroit. Bien que n'étant pas les prédateurs les plus rapides, les zombies sont capables de s'approcher, mourir et mourir aux humains. Les humains morts dans les mains des zombies deviennent des zombies et ainsi leur tribu augmente. Dans cette situation les êtres humains se dispersent, se forment des collectivités isolées et le monde devient un lieu redouté par les zombies.
The Walking Dead est une série développée par Frank Darabonte, basée sur les bandes dessinées de Robert Kirkman et Tony Moore. Après s'être réveillé de la coma dans un ancien hôpital, la police Rick Grimes ne trouve pas le monde qu'elle a laissé avant d'être dans le coma, mais celui détruit par une épidémie de zombies. Dans la banlieue d'Atlanta, un groupe de survivants de la peste lutte pour survivre, dirigé par Rick. Votre rêve est de chercher une terre sans zombies. Dans une situation de plus en plus célèbre, et alors que le désespoir s'impose, l'instinct de survie les conduit à tout. Les zombies sont la bête chasseuse de cette section et veulent attraper l'homme.
Un modèle mathématique simplifié de prédateurs et de proies
Si l'on veut éviter l'extinction définitive de parasites et/ou d'espèces minoritaires dans une communauté, il faut se fixer sur l'augmentation ou la diminution de la densité de population. Les cycles de population sont des instruments indispensables pour comprendre les variations de densité de population et prévoir les changements qui se produiront dans une période de temps, où la population d'une espèce croît et diminue de façon récurrente. Ainsi, les modèles de prédateurs et de proies ont été une partie importante de ces recherches et expriment l'effort de modéliser l'écologie par des modèles mathématiques. Alfred Lotka et Vito Volterra ont été chargés de proposer un modèle mathématique simplifié de rapaces et de proies.
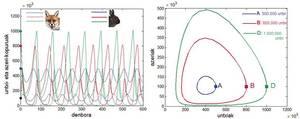
Supposons qu'un prédateur, par exemple des renards, ne mange que des lapins et qu'à l'instant il y a une population de renards a(t) et une population de lapins u(t). En l'absence de lapins, les renards mourraient en accord avec l'équation différentielle a'(t) =- .a(t), la constante -{ le paramètre de différence entre le taux de natalité et la mortalité des renards. En l'absence d'aciers, la population de lapin grandirait exponentiellement en suivant l'équation différentielle u'(t)=?.u(t), étant ? le paramètre de différence entre le taux de natalité et la mortalité des lapins.
Si l'on veut modeler la situation dans laquelle les quantités des deux populations sont positives, dans l'équation différentielle des renards il faudra ajouter un additif qui sera positif quand il y aura des lapins et combien plus de lapins il y aura plus. En outre, ce commandant devra être haut quand le nombre de lapins et de renards sont élevés. En outre, un autre additif doit être ajouté à l'équation différentielle des lapins. Dans ce cas, l'addition que nous ajouterons sera négative dans une situation où il y a des renards: quand il y aura des renards, les renards mangeront des lapins et donc diminuera le nombre de lapins. De plus, plus le nombre de renards est élevé, plus le nombre de lapins diminue, de sorte que cette addition négative doit être proportionnelle au nombre de renards. Compte tenu de cela, et étant donné que les chiffres initiaux des lapins et des renards sont u(0) et a(0), le modèle des prédateurs et des proies est appelé modèle Lotka-Volterra et est donné par:
u'(t) = u(t)(?-?a(t)
a'(t) = -a(t)(})
Il s'agit d'un modèle avec un sens, car comme le nombre de renards augmente le rythme qui change le nombre de lapins, c'est-à-dire u'(t), diminue et lorsque le nombre de lapins augmente, la vitesse de reproduction des lapins augmente. Il s'agit d'un système d'équations différentielles avec un résultat cyclique: si des lapins sont ajoutés, le nombre de renards augmentera en raison de l'augmentation de la nourriture et lorsque le nombre de renards augmentera. La diminution des lapins entraînera une diminution des renards, ce qui entraînera une augmentation des lapins que nous reviendrons au point initial en terminant le cycle.
L'équilibre dans ce modèle se produit quand aucune des deux populations n'est altérée, c'est-à-dire quand les deux dérivées valent zéro. Cela se produit lorsque le nombre de lapins et le nombre de renards sont nuls, u(t) = a(t) = 0, ou a (t) = ?/b et u(t) ={/?. Dans la première solution, les deux espèces disparaissent; dans la seconde, le nombre des deux populations reste fixe dans le temps.
Mais ces cycles sont-ils habituels dans la nature ? Ce modèle est-il capable de prédire correctement les changements de population ? La réponse est négative, car le modèle de capture unique présenté est trop simplifié. Dans la réalité, il y a un contexte dans lequel il y a plus d'un prédateur et une proie, et il devient très complexe. Cependant, bien que le modèle Lotka-Volterra n'ait pas correctement modelé ce qui se passe dans le monde réel, il a cédé la place à des modèles plus complexes de prédateurs et de proies qui ont contribué à une meilleure compréhension de la communauté écologique et à la régularisation des cycles de prédateurs et de proies.
Certains modèles mathématiques d'une épidémie de zombies
Modèle de base
Un des exemples utilisés dans la modélisation de densités de population par des modèles mathématiques est celui des zombies. Lorsque le modèle des prédateurs et des proies est constitué de zombies et d'êtres humains, trois groupes peuvent être considérés: celui des êtres humains (G), celui des zombies (Z) et celui des humains morts et des zombies (H). Dans ce modèle on suppose que le nombre d'êtres humains augmente par le taux de natalité (que nous appellerons©) et diminue pour deux raisons : pour des causes naturelles et pour l'influence des zombies. Le nombre de zombies diminue par l'action humaine, c'est-à-dire parce que les humains peuvent les tuer. Les êtres humains et les zombies morts, que ce soit pour des causes naturelles ou entre les mains de zombies, formeront le groupe H. Les êtres de ce groupe peuvent ressusciter et devenir des zombies. Ainsi, les chances d'élargir l'ensemble des zombies sont deux: transformer les humains en zombies en interaction avec les zombies et convertir ceux du groupe de morts en zombies.
La formulation de ce modèle se fait par trois équations différentielles, et la somme des changements dans les trois groupes fournit l'indice de naissance des êtres humains G'+Z'+H' =©. Cela signifie qu'avec le passage du temps la somme des quantités des trois groupes sera infinie. Ou ce qu'il en est de même, quand t??ltima, G+Z+Hâ ser?? br class="xliff-newline" /?0 ). Comme le nombre d'êtres humains ne tend pas à l'infini, infini sera la somme des deux autres groupes, ce qui signifie que l'épidémie de zombies finira avec la civilisation.
Modèle avec infection
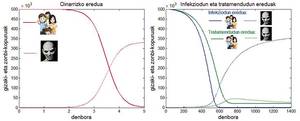
Le modèle que nous venons de décrire est très basique et il est possible de construire des modèles plus réalistes que lui. Par exemple, dans l'un de ces modèles, on peut considérer que lorsque le zombie contamine l'homme, l'homme ne devient pas immédiatement zombie, mais, après une période de temps comme pollué, l'homme peut mourir ou devenir zombie. Comme dans le modèle de base, si le taux de natalité humaine n'est pas nul, dans ce modèle l'épidémie de zombies provoquera la disparition des êtres humains, bien que dans ce cas il faudra plus de temps que dans le précédent.
Modèle avec traitement
Dans les deux modèles observés jusqu'à présent (basique et infectieuse), plus ou moins vite le monde reste sans humains et les zombies s'approprient le monde. Mais est-il possible de penser à un modèle dans lequel les deux espèces cohabitent?
Dans le sable où il y a un groupe de personnes infectées ou infectées, nous ajouterons un traitement curatif aux humains. Ce traitement peut amener les zombies à l'état humain. Cela ne veut pas dire qu'une fois convertis en êtres humains, ils ne peuvent plus être des zombies. Autrement dit, le traitement n'implique pas l'immunité. Si nous analysons la situation du traitement, nous constatons que le traitement ne peut pas non plus entraîner la disparition du nombre de zombies. Les zombies existeront, mais l'homme ne disparaîtra pas du monde. C'est-à-dire que, dans un modèle dans lequel il y a un traitement, les deux espèces convergeront dans le monde.
Le monde dépend des zombies ou des êtres humains ?
Qui prévaudra dans un contexte de science-fiction ? Les zombies prédomineront-ils, comme l'indique le modèle mathématique, ou, comme nous sommes dans la fiction, l'être humain affrontera les zombies ? Ici, au moins, nous avons donné une idée aux scénaristes de The Walking Dead pour que la série continue.
Mais est-il possible de mettre fin à la peste des zombies? Et, s'il y en a, les scénaristes de série seront-ils arrivés à un de ces modèles qui éliminera les zombies pour toujours ?
Il ya des modèles dans lesquels l'homme prévaut sur les zombies. Qui peut penser à un tel modèle? Ceux de la série The Walking Dead semblent connaître un exemple d'eux, ce qui peut dériver que l'être humain n'a pas complètement disparu dans les trois saisons que la série porte.
Bibliographie Bibliographie

Gai honi buruzko eduki gehiago
Elhuyarrek garatutako teknologia






