¿Seríamos capaces de combatir una epidemia de zombis?
2013/04/01 Alberdi Celaya, Elisabete - Matematikan lizentziatua eta doktoregaia Iturria: Elhuyar aldizkaria

The Walking Dead
Varias historias de ciencia ficción narran apocalipsis de zombis. En estos casos, tras la muerte del hombre se resucita y se convierte en zombi. En la mayoría de los casos, estos seres resucitados, los zombis, son humanos o caníbales. Son torpes, con la mirada medio perdida, con las manos hacia delante caminando y se mueven torpes. A pesar de no ser los depredadores más rápidos, los zombis son capaces de acercarse, morir y morir a los humanos. Los humanos muertos en manos de los zombis se convierten en zombies y así su tribu aumenta. En esta situación los seres humanos se dispersan, se forman colectividades aisladas y el mundo se convierte en un lugar temido por los zombis.
The Walking Dead es una serie desarrollada por Frank Darabonte, basada en los cómics de Robert Kirkman y Tony Moore. Tras despertarse de la coma en un viejo hospital, la policía Rick Grimes no encuentra el mundo que dejó antes de estar en coma, sino el destruido por una epidemia de zombis. En los suburbios de Atlanta, un grupo de supervivientes de la peste lucha por sobrevivir, liderado por Rick. Su sueño es buscar una tierra sin zombies. En una situación cada vez más famosa, y mientras la desesperación se impone, el instinto de supervivencia les lleva a cualquier cosa. Los zombis son la bestia cazadora de esta sección y quieren atrapar al hombre.
Un modelo matemático simplificado de predadores y presas
Si se quiere evitar la extinción definitiva de plagas y/o especies minoritarias en una comunidad, hay que fijarse en el aumento o disminución de la densidad de población. Los ciclos de población son instrumentos imprescindibles para comprender las variaciones de la densidad de población y prever los cambios que se producirán en un período de tiempo, en los que la población de una especie crece y disminuye de forma recurrente. Así, los modelos de predadores y presas han sido una parte importante de estas investigaciones y expresan el esfuerzo de modelar la ecología mediante modelos matemáticos. Alfred Lotka y Vito Volterra fueron los encargados de proponer un modelo matemático simplificado de rapaces y presas.
Supongamos que un depredador, por ejemplo zorros, come únicamente conejos y que en el instante t hay población de zorros a(t) y población de conejos u(t). En ausencia de conejos, los zorros morirían de acuerdo con la ecuación diferencial a'(t) = -> .a(t), siendo la constante -{ el parámetro de diferencia entre la tasa de natalidad y la mortalidad de los zorros. En ausencia de aceros, la población de conejo crecería exponencialmente siguiendo la ecuación diferencial u'(t)=?.u(t), siendo ? el parámetro de diferencia entre la tasa de natalidad y la mortalidad de los conejos.
Si se quiere modelar la situación en la que las cantidades de ambas poblaciones son positivas, en la ecuación diferencial de los zorros habrá que añadir un sumando que será positivo cuando haya conejos y cuantos más conejos haya más. Además, este sumando deberá ser alto cuando el número de conejos y de zorros sean elevados. Asimismo, en la ecuación diferencial de los conejos deberá añadirse otro sumando. En este caso, el sumando que añadiremos será negativo en una situación en la que hay zorros: cuando haya zorros, los zorros comerán conejos y, por tanto, disminuirá el número de conejos. Además, cuanto mayor sea el número de zorros, mayor será la disminución del número de conejos, por lo que este sumando negativo deberá ser proporcional al número de zorros. Teniendo en cuenta esto, y teniendo en cuenta que las cifras iniciales de conejos y zorros son u(0) y a(0), el modelo de predadores y presas se denomina modelo Lotka-Volterra y viene dado por:
u'(t) = u(t)(?-?a(t)
a'(t) = -a(t)(})
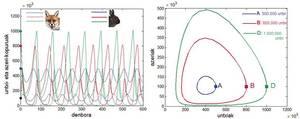
Se trata de un modelo con sentido, ya que a medida que aumenta el número de zorros el ritmo que cambia el número de conejos, es decir, u'(t), disminuye y cuando aumenta el número de conejos aumenta la velocidad de reproducción de los conejos. Se trata de un sistema de ecuaciones diferenciales con resultado cíclico: si se añaden conejos, el número de zorros aumentará debido al aumento de la comida y cuando el número de zorros aumente disminuirá. La disminución de los conejos supondrá una disminución de los zorros, lo que provocará un aumento de los conejos que volveremos a estar en el punto inicial completando el ciclo.
El equilibrio en este modelo se produce cuando no se alteran ninguna de las dos poblaciones, es decir, cuando ambas derivadas valen cero. Esto ocurre cuando el número de conejos y el número de zorros son nulos, u(t) = a(t) = 0, o a (t) = ?/b y u(t) ={/?. En la primera solución, ambas especies desaparecen; en la segunda, el número de ambas poblaciones permanece fijo en el tiempo.
¿Pero estos ciclos son habituales en la naturaleza? ¿Es capaz este modelo de predecir adecuadamente los cambios de población? La respuesta es negativa, ya que el modelo de captura única y de captura única presentado es demasiado simplificado. En la realidad se da un contexto en el que hay más de un depredador y una presa, y se hace muy complejo. Sin embargo, a pesar de que el modelo Lotka-Volterra no ha modelado adecuadamente lo que ocurre en el mundo real, ha dado paso a modelos más complejos de predadores y presas que han contribuido a una mejor comprensión de la comunidad ecológica y a la regularización de los ciclos de predadores y presas.
Algunos modelos matemáticos de una epidemia de zombis
Modelo básico
Uno de los ejemplos utilizados en el modelado de densidades de población mediante modelos matemáticos es el de los zombis. Cuando el modelo de predadores y presas está formado por zombis y seres humanos, se pueden considerar tres grupos: el de los seres humanos (G), el de los zombies (Z) y el de los humanos muertos y zombies (H). En este modelo se supone que el número de seres humanos aumenta por el índice de natalidad (que llamaremos©) y disminuye por dos motivos: por causas naturales y por la influencia de los zombis. El número de zombis disminuye por la acción humana, es decir, porque los seres humanos pueden matarlos. Los seres humanos y los zombies muertos, tanto por causas naturales como en manos de zombis, formarán el grupo H. Los seres de este grupo pueden resucitar y convertirse en zombis. Así, las posibilidades de ampliar el conjunto de zombis son dos: transformar a los seres humanos en zombies en interacción con los zombies y convertir a los del grupo de muertos en zombis.
La formulación de este modelo se realiza mediante tres ecuaciones diferenciales, y la suma de los cambios en los tres grupos proporciona el índice de nacimiento de los seres humanos G'+Z'+H' =©. Esto significa que con el paso del tiempo la suma de las cantidades de los tres grupos será infinita. O lo que es lo mismo, cuando t??ltima, G+Z+Hâ> ser?? <br class="xliff-newline" /> 0 ). Como el número de seres humanos no tiende al infinito, infinito será la suma de los otros dos grupos, lo que significa que la epidemia de los zombis acabará con la civilización.
Modelo con infección
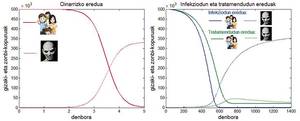
El modelo que acabamos de describir es muy básico y es posible construir modelos más realistas que él. Por ejemplo, en uno de esos modelos se puede considerar que cuando el zombis contamina al hombre, el hombre no se convierte inmediatamente en zombi, sino que, tras un período de tiempo como contaminado, el hombre puede morir o convertirse en zombi. Al igual que en el modelo básico, si la tasa de natalidad humana no es nula, en este modelo la epidemia de zombis provocará la desaparición de los seres humanos, aunque en este caso se tardará más tiempo que en el anterior.
Modelo con tratamiento
En los dos modelos observados hasta ahora (básico e infeccioso), más o menos rápido el mundo queda sin seres humanos y los zombis se apropian del mundo. Pero, ¿es posible pensar en un modelo en el que ambas especies convivan?
En la arena en la que existe un grupo de infectados o infectados añadiremos un tratamiento curativo para los seres humanos. Este tratamiento puede llevar los zombis a estado humano. Esto no quiere decir que una vez convertidos en seres humanos no puedan volver a ser zombies. Es decir, el tratamiento no implica inmunidad. Si analizamos la situación en la que se encuentra el tratamiento, observaremos que el tratamiento tampoco puede provocar la desaparición del número de zombis. Los zombis existirán, pero el hombre no desaparecerá del mundo. Es decir, en un modelo en el que hay tratamiento convivirán las dos especies en el mundo.
¿El mundo depende de los zombis o de los seres humanos?
¿A quién va a prevalecer en un contexto de ciencia ficción? ¿Predominarán los zombis, tal y como indica el modelo matemático, o, como estamos en la ficción, el ser humano se enfrentará a los zombies? Aquí, al menos, hemos dado alguna idea a los guionistas de The Walking Dead para que la serie continúe.
Pero, ¿es posible acabar con la peste de los zombis? Y, si hay, ¿se les ocurrirá a los guionistas de serie alguno de esos modelos que eliminará los zombis para siempre?
Hay modelos en los que el hombre prevalece sobre los zombies. ¿Quién puede pensar en un modelo así? Los de la serie The Walking Dead parecen conocer algún ejemplo de ellos, lo que puede derivar en que el ser humano no haya desaparecido completamente en las tres temporadas que lleva la serie.
Bibliografía

Gai honi buruzko eduki gehiago
Elhuyarrek garatutako teknologia






