Zonbien izurrite bati aurre egiteko gai izango ote ginateke?

The Walking Dead

Zientzia-fikziozko hainbat istoriotan zonbien apokalipsiak kontatzen dira. Halakoetan, gizakia hil ondoren berpiztu egiten da, eta zonbi bilakatzen da. Gehienetan, berpiztutako gizaki hauek, zonbiak alegia, gizajaleak edo kanibalak dira. Baldarrak dira, begirada erdi galdua dute, eskuak aurrerantz dituztela egiten dute oinez eta trakets mugitzen dira. Harraparirik bizkorrenak izan ez arren, zonbiak gai dira gizakiengana hurbildu, haginka egin eta hiltzeko. Zonbien eskuetan hildako gizakiak zonbi bihurtzen dira eta horrela haien tribua ugarituz joaten da. Egoera horretan, gizakiak sakabanatu egiten dira, gizatalde isolatuak sortzen dira eta mundua zonbien beldur den toki bilakatzen da.

Frank Darabont-ek garatutako telesaila da The Walking Dead , eta Robert Kirkman eta Tony Moore-ren komikiak ditu oinarri. Ospitale zahar batean koma-egoeratik esnatu ondoren, Rick Grimes poliziak ez du koman egon aurretik utzi zuen mundua aurkitzen, zonbien izurrite batek suntsitutakoa baizik. Atlantako aldirietan, izurritetik bizirik atera den giza taldetxo batek bizirik irauteko ahaleginean dihardu, eta Rick izango da talde hori gidatuko duena. Zonbirik gabeko lurra bilatzea dute amets. Egoera gero eta ospelago batean, eta etsipena nagusitzen zaien bitartean, bizirik irauteko senak edozer egitera bultzatzen ditu. Zonbiak dira sail honetako piztia harrapatzaileak, eta gizakia nahi dute harrapatu.

Harrapari eta harrapakinen eredu matematiko sinplifikatu bat

Komunitate batean izurriteak edota espezie gutxituen behin betiko desagertzea ekidin nahi badira, populazio-dentsitatearen hazkundeari edo jaitsierari erreparatu behar zaio. Populazio-dentsitatearen gorabeherak ulertzeko eta denboraldi batean izango diren aldaketak aurreikusteko ezinbesteko tresnak dira populazioaren zikloak, zeintzuetan espezie bateko populazioa behin eta berriro hazten eta txikitzen den. Hala, harrapari eta harrapakinen ereduak ikerketa hauetako parte garrantzitsua izan dira, eta ekologia eredu matematikoen bidez modelatzeko ahalegina adierazten dute. Alfred Lotka eta Vito Volterra izan ziren harraparien eta harrapakinen eredu matematiko sinplifikatu bat proposatu zutenak.

Jo dezagun harrapari batek --adibidez, azeriak-- bakarrik untxiak jaten dituela eta t aldiunean a(t) azeri-populazioa eta u(t) untxi-populazioa daudela. Untxirik ezean, azeriak ekuazio diferentzial honi jarraikiz hilko lirateke: a'(t) = -γ.a(t), -γ konstantea azerien jaiotze-tasaren eta heriotza-tasaren arteko diferentzia-parametroa izanik. Azeririk ezean, untxi-populazioa esponentzialki haziko litzateke u'(t)=α.u(t) ekuazio diferentzialari jarraituz, α untxien jaiotze-tasaren eta heriotza-tasaren arteko diferentzia-parametroa izanik.

Populazio bien kantitateak positiboak diren egoera modelatu nahi bada, azerien ekuazio diferentzialean batugai bat gehitu beharko da, untxiak daudenean positiboa izango dena eta zenbat eta untxi gehiago egon handiagoa izango dena. Gainera, batugai horrek handia izan beharko du untxi-kopurua eta azeri-kopurua handiak direnean. Era berean, untxien ekuazio diferentzialean ere beste batugai bat erantsi beharko da. Kasu honetan, erantsiko dugun batugaia negatiboa izango da, azeriak dauden egoera batean: azeriak daudenean, azeriek untxiak jango baitituzte eta, ondorioz, gutxitu egingo baita untxi-kopurua. Gainera, zenbat eta azeri gehiago izan untxi-kopurua orduan eta gehiago gutxituko denez, batugai negatibo horrek azeri-kopuruaren araberakoa izan beharko du. Hori kontuan hartuz eta hasierako untxi- eta azeri-kopuruak u(0) eta a(0) direla kontuan hartuz sortzen den harrapari eta harrapakinen ereduari Lotka-Volterra eredu deritzo, eta honela emana dator:

Lotka-Volterra ekuazioen emaitza hasierako balio jakin batzuetarako. Irudiaren ezkerraldean 100.000 azeri eta 500.000, 800.000 eta 1.000.000 untxi dauden hasierako populazioei dagozkien untxi- eta azeri-kopuruak denboran irudikatu dira. Irudiaren eskuineko aldean, hasierako balio-bikote bakoitzerako untxi- eta azeri-kopuruak irudikatu dira. Hasierako untxi- eta azeri-kopuruak 'å' sinboloa erabilita irudikatu dira. Arg. © Elisabete Alberdi

u'(t) = u(t)(α-βa(t))

a'(t) = -a(t)(γ-δu(t))

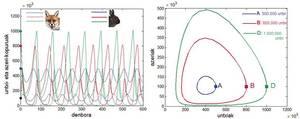
Zentzua duen eredua da, azeri-kopurua handitu ahala untxi-kopurua aldatzen den erritmoa, hau da u'(t), txikituz baitoa, eta untxi-kopurua handitzen denean untxiak ugaltzen diren abiadura ere handitu egiten baita. Emaitza ziklikodun ekuazio diferentzialen sistema da hori: untxiak gehitzen badira, azeri-kopurua handitu egingo da janari gehiago izango dutelako; eta azeri-kopurua handitzen denean, gutxitu egingo dira untxiak. Untxien gutxitzeak azerien gutxitzea ekarriko du, eta horrek untxien gehitzea, eta berriz hasierako puntuan izango gara zikloa osatuz.

Eredu horretako oreka populazio bata ez bestea aldatzen ez direnean gertatzen da, hau da, deribatu biek zero balio dutenean. Eta hori gertatzen da untxi-kopurua eta azeri-kopurua nuluak direnean, u(t) = a(t) = 0, edota a (t) = α/β eta u(t) = γ/δ gertatzen direnean. Lehenengo soluzioan, espezie biak desagertzen dira; bigarrenean, populazio bien kopuruek finko diraute denboran.

Baina halako zikloak ohikoak al dira naturan? Gai al da eredu hori populazio-aldaketak era egokian iragartzeko? Erantzuna ezezkoa da, aurkeztu dugun harrapatzaile bakarreko eta harrapatu bakarreko eredua sinplifikatuegia baita. Errealitatean, harrapari eta harrapakin bat baino gehiago dagoen testuingurua gertatzen da, eta oso konplexu bihurtzen da. Nolanahi ere, nahiz eta Lotka-Volterra ereduak mundu errealean gertatzen dena era egokian modelatu ez, harrapari eta harrapakinen eredu konplexuagoei bide eman die eta eredu konplexuago horiek komunitate ekologikoa hobeto ulertzen eta harrapari eta harrapakinen zikloak erregularizatzen lagundu dute.

Zonbi-izurrite bateko zenbait eredu matematiko

Oinarrizko eredua

Gizaki-zonbi eredu bakoitzari dagozkion soluzio-kurbak: ezkerrean, oinarrizko ereduari dagozkion soluzio-kurbak, eta eskuinean, infekziodun ereduari eta tratamendudunari dagozkienak. Hasierako baliotzat, hauek hartu dira: gizaki-kopurua 500.000, zonbi-kopurua 0, infekziodunen kopurua 0 eta hildakoen kopurua 100.000. Kasu guztietan, konstante-sorta berdina erabili da (α, β, δ, ς, ρ eta c). Arg. © Elisabete Alberdi

Populazio-dentsitateak eredu matematikoen bidez modelatzerakoan erabili izan den adibideetako bat zonbiena da. Harrapari eta harrapakinen eredua zonbiek eta gizakiek osatzen dutenean, hiru multzo kontsidera daitezke: gizakien multzoa (G), zonbiena (Z) eta hildako gizakiek eta hildako zonbiek osatutakoa (H). Eredu honetan joko dugu gizaki-kopurua jaiotze-indizeagatik handitzen dela (Π deituko duguna) eta bi arrazoirengatik gutxitzen dela: kausa naturalengatik eta zonbien eraginagatik. Zonbien kopurua gizakien eraginagatik gutxitzen da, gizakiek haiek hil ditzaketelako, alegia. Kausa naturalen eraginez zein zonbien eskuetan hildako gizakiek eta hildako zonbiek H multzoa osatuko dute. Multzo horretako izakiak berpiztu eta zonbi bihur daitezke. Hala, zonbien multzoa ugaritzeko dauden aukerak bi dira: bata, gizakiak zonbiekin elkarrekintzan zonbi bihurtzea, eta bestea, hildakoen multzokoak zonbi bihurtzea.

Eredu honen formulazioa hiru ekuazio diferentzialen bidez egiten da, eta hiru multzoen aldaketen baturak gizakien jaiotze-indizea ematen du G'+Z'+H' = Π. Horrek esan nahi du denbora pasatu ahala hiru multzoen kopuruen batura infinitu izango dela. Hau da, tÆ ` denean, G+Z+HÆ ` izango da, baldin eta gizakien jaiotze-tasa nulua ez bada (hau da, Π ? 0 ). Gizakien kopuruak infiniturantz jotzen ez duenez, beste multzo bien batura izango da infinitu, eta horrek esan nahi du zonbien izurriteak zibilizazioaren amaiera ekarriko duela.

Infekziodunak dauden eredua

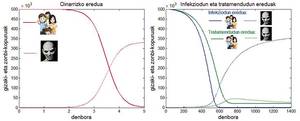
Deskribatu berri dugun eredua oso oinarrizkoa da, eta bera baino eredu errealistagoak eraikitzea posiblea da. Adibidez, horietako eredu batean jo daiteke zonbiak gizakia kutsatzen duenean gizakia ez dela segituan zonbi bihurtzen, baizik eta, kutsatu gisa denbora-tarte batez egon ondoren, gizakia hil egin daitekeela edo zonbi bihur daitekeela. Oinarrizko ereduan bezala, gizakien jaiotze-tasa nulua ez bada, eredu honetan ere zonbien izurriteak gizakien desagertzea ekarriko du, nahiz eta kasu honetan aurrekoan baino denbora gehiago behar izango den hori gertatzeko.

Tratamendudun eredua

Orain arte ikusitako eredu bietan (oinarrizkoan eta infekziodunean), arinago edo beranduago mundua gizakirik barik geratzen da, eta zonbiak munduaren jabe egiten dira. Baina, posible al da espezie biak batera biziko diren eredu batean pentsatzea?

Formulazio matematikoen laburpena. Arg. © Elisabete Alberdi

Infektatuen edo kutsatuen multzo bat existitzen den jokalekuan, gizakiak sendatzeko tratamendu bat erantsiko dugu. Tratamendu horrek zonbiak gizaki-egoerara eraman ahal izango ditu. Horrek ez du esan nahi, ordea, behin gizaki bihurtuta berriz zonbi bihur ezin daitezkeenik. Hau da, tratamenduak ez dakar berekin immunitatea. Tratamendua dagoen egoera aztertzen badugu, ohartuko gara tratamenduak ere ezin duela zonbi-kopurua desagertzea eragin. Zonbiak existituko dira, baina gizakia ez da mundutik guztiz desagertuko. Hau da, tratamendua dagoen eredu batean bi espezieak biziko dira munduan.

Mundua zonbien esku ala gizakien esku?

Zientzia-fikziozko testuinguru batean nor gailenduko ote da? Zonbiak nagusituko dira, eredu matematikoak dioen bezala, ala, fikzioan gabiltzanez, aurre egingo die gizakiak zonbiei? Hemen, behintzat, The Walking Dead serieko gidoilariei ideiaren bat eman diegu serieak aurrera jarrai dezan.

Baina, ba ote dago zonbien izurriteaz guztiz bukatzeko aukerarik? Eta, egotekotan, bururatuko ote zaie serieko gidoilariei zonbiak betiko deuseztatuko dituen eredu horietakoren bat?

Egon badaude ereduak zeintzuetan gizakia zonbiei gailentzen zaien. Nork pentsa dezake horrelako eredu batean? Badirudi The Walking Dead seriekoek horietako ereduren baten jakitun direla, eta horren ondorioa izan daiteke serieak daramatzan hiru denboraldietan gizakiak guztiz desagertu ez izana.

Bibliografia