"Débute" 300 ans (2) Isaac Newton, créateur du calcul

1987/04/01 Duoandikoetxea Zuazo, Javier - EHUko matematika irakaslea Iturria: Elhuyar aldizkaria

• Fisika

Marcher à pied

Le Grec Mathematical, largement basé sur la géométrie, semble normal de vouloir calculer la surface des figures plates et le volume des solides. De même, en faisant les premiers pas de la physique, ils ont montré un intérêt pour obtenir un centre de gravité. La plupart de ces problèmes sont dus à Archimède, un serviteur (a. C.). III. Au XIXe siècle) : surfaces d'ellipses et segments paraboliques, volume de nombreux solides de révolution (sphère, ellipsoïde, segment de paraboles, etc.) et le centre de gravité de la majorité, par exemple.

Mais Archimède n'avait pas la formulation facile offerte par le calcul actuel (l'intégrale d'une seule fonction a comme conséquence plusieurs résultats d'Archimède) et chaque problème était nouveau pour lui. Pour l'obtention des résultats, il a utilisé son intuition géométrique, décomposant souvent l'image en très petits fragments et les rapprochant par des figures connues (triangles, carrés, cylindres). Plus tard, pour le justifier, il utilisait la "méthode exhacutive" adoptée par Eudel.

Bientôt les mathématiques (au moins celles liées au calcul) sont restées endormies et avec elle les travaux d'Archimède. Les Arabes ont apporté ces œuvres à l'ouest de l'Europe, où il était le XVI. Au XXe siècle, ils reprirent leur étude. XVII. On peut dire qu'au début du XXe siècle on comprenait les œuvres d'Archimède, au moins assez pour porter de nouveaux fruits. Dans ces cinquante années jusqu'à ce que Newton a été accumulé noms et sauvé: Kepler, Cavalieri, Torricelli, Roberval, Descartes, Fermat, Pascal, Wallis, Barrow, etc.

De la main de Descartes, la géométrie analytique a une grande influence sur le calcul, puisque l'expression algébrique des courbes a provoqué une nouvelle formulation agile de problèmes. Une étape importante a été celle de la classification des problèmes, avec deux grands groupes: les problèmes de tangentes et les problèmes de surfaces, qui les reçoivent des modèles principaux. Les problèmes du premier groupe (rectifier une courbe à un point ou calculer le maximum et le minimum) étaient pratiquement nouveaux, car dans les mathématiques anciennes ils n'apparaissent pas et sont résolus par la dérivée. Ceux du deuxième groupe, cependant, sont formulés par Archimède et aujourd'hui nous les associons à l'intégration.

Parmi les mathématiciens mentionnés ci-dessus, Fermat a été le plus avancé dans la résolution de ces problèmes. Pour le calcul des maxima et minima, par exemple, a donné la méthode suivante: Trouver la valeur A pour laquelle [F(A + E) - F (A)] / E = 0, en faisant E = 0 (après avoir obtenu le rapport). Bien qu'il semble un dérivé, il n'y a pas de limite ici, puisque Fermat le fait pour les polynômes, où le quotient est toujours exact. En intégration, aujourd'hui

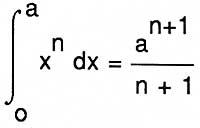
Il connaissait l'équivalent géométrique de la formule, quelque chose prouvé à Cavalieri, Pascal ou Roberval.

Et Newton arriva

Le jeune Newton a connu et bientôt maîtrisé les techniques des livres de mathématiques en lisant son propre livre. Cette formation autodidactique n'est pas surprenante, étant donné que dans les Universités, il n'y avait pas de cours ordinaires sur ce sujet. Quoi qu'il en soit, Barrow collaborerait à la fois à la sélection des livres et au cours qu'il a enseigné pendant un an. Cependant, il est connu qu'ils sont passés de la main de Newton alors et qu'il avait une grande influence de deux: La géométrie de Descartes et celle des livres "Arithmetica Infinitorum" de Wallis.

Mais Newton devançait tout le monde en 1665-66 ans, car jusqu'alors il avait vu comme personne la clé des problèmes et la solution était de donner une règle pour faire la dérivée, démontrer que l'intégrale était l'inverse de la dérivée et indiquer la voie d'application dans différents problèmes.

Newton mesurait toutes les quantités variables par rapport au temps (plus tard il a dit que le temps est n'importe quelle quantité changeant uniformément) : elles étaient fluentes. Les vitesses de changement étaient appelées flux. Une courbe laun est due au mouvement de l'abscisa et ordonnée et x et y ont leurs flux x et y. Compte tenu de l'équation de la courbe, la relation entre les flux est recherchée. Comment allez-vous l'obtenir? Remplacer x et y par x + x ou e et + et ou dans l'équation de la courbe pour raccourcir l'initiale, diviser par ou et faire 0 celle-ci ou. La méthode, en plus du style, est l'actuelle, avec la possibilité de réaliser une dérivée implicite.

Par exemple, pour dériver y = x m/n, appliquez sa méthode à la relation yn = xm: Après avoir traité les deux côtés de l'égalité (et + et ou ) n = (x + x ou ) m avec la formule du binôme, après diviser et n et x m éliminés par ou, et annulaire dit ou, obtient n et n-1 et = m x m-1 x. Il suffit de remplacer et par x m/n,

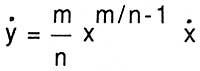
pour avoir une dérivée connue.

Le théorème de base du calcul ou l'inverse de l'intégration et la dérivation, a été formulé géométriquement par Barrow dans le livre "Lectiones Geometricae" (publié en 1670), mais il ne semble pas s'approprier sa valeur. "La formule de Newton-Leibniz" est sa présentation la plus simple: Si F' = f,

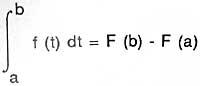
ou bien,

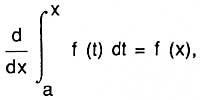
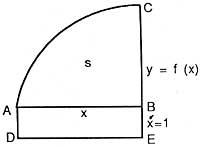
c'est-à-dire, la dérivée de l'abscisa de la surface est fonction (ou ordonnée). Voyons la formulation de Newton. Biz y = f (x) courbe et s = surface (ABC) (voir figure), qui est généré par le mouvement parallèle de la droite verticale BC. Biz x = AB et faisons le parallélogramme ABED en considérant AD = 1. Donc x = surface (ABDE), cette surface est générée par le mouvement de la VE. Selon Newton, la vitesse d'incrémentation des deux surfaces est égale à la relation BC et BE, c'est-à-dire s/x = BC/BE = f(x).

Une fois cela décidé, étant plus facile à dériver, la table des intégrales contiendra les dérivés à l'envers. De cette façon, cependant, de nombreuses courbes ne peuvent pas encore être intégrées et suite à une idée prise de Wallis pour élargir les possibilités, il a examiné les développements sériés des fonctions et les a suivis pour obtenir une nouvelle série de sujets intégrés (sans tenir compte des problèmes de convergence, bien sûr).

L'expansion de (1 + x) m, quand m est total, bien qu'il soit appelé binôme de Newton, est vraiment intéressant quand m est incomplet, alors le polynôme n'est pas une série infinie. m au milieu de deux nombres entiers (1/2, 3/2, ...) est déjà dû à Newton la réponse de l'affaire, car il a prouvé qu'il applique la même règle que les coefficients des polynômes pour les coefficients.

Afin de se fonder sur ce qui était fait, Newton fera référence aux relations des augmentations: flux " la première relation des augmentations émergentes " ou " la dernière relation des augmentations fongibles ". À la vue de l'image, supposons que nous avançons un peu l'abscise, alors la surface augmente et il faut obtenir un rapport entre les augmentations de surface et abscise, mais le premier rapport coule est ", avant de commencer à se déplacer ... De même, considérant le processus en arrière, les augmentations disparaissent et le dernier rapport des augmentations destructives " est le flux. On peut susciter l'idée de limite indéterminée.

Il faut partager les honneurs

Parmi les œuvres de Newton, celles liées au Calcul sont: "De Analysi per Aequationes Numero Terminorum Infinitas" (écrit vers 1669, publié en 1711), "Methodus Fluxionum et Serierum Infinitorum" (écrit en 1671, publié en 1736), "Tractatus de Quadratura Curvarum" (écrit en 1693, pages 1704) et "principi" (p. Comme on le voit, ils ont passé vingt ans entre l'obtention des rachetés et leur licenciement, et ainsi, en 1675, Leibniz est venu de leur côté à ressembler. Le premier article de Leibniz a été publié en 1684, anticipant pendant trois ans "Principia".

En 1698 Fatio de Duillier, ami de Newton, a publié un livre dans lequel il a reconnu tout le mérite en dénonçant que Leibniz avait fait plagiat. Leibniz lui-même défendu et a passé dix ans jusqu'à ce que la deuxième attaque est venu dans un article de Keill. Cet article parut dans la revue de la Real Sociedad et Leibniz, comme associé, demanda en 1711 au secrétaire de clarifier le problème.

Lorsque le président était Newton, un comité a été nommé et la décision de la commission a été encore plus difficile pour Leibniz. En outre, ils ont décidé de publier la collection de lettres "Commercium Epistolicum" contre Leibniz. Le débat s'est élargi et certaines personnes de Leibniz ont remarqué quelques erreurs de Newton. Leibniz, en 1714, a écrit le programme " Histoire et origo Calculi differentialis " pour raconter sa vérité. Malgré sa mort deux ans plus tard, Newton a continué à attaquer.

XX. Jusqu'au XIXe siècle, ce point a été indécis, mais lorsque les manuscrits de Leibniz ont été analysés, il a été définitivement reconnu son mérite et aujourd'hui à la fois l'honneur d'être créateurs du Calcul. Le débat, cependant, a affecté plus l'Angleterre, où les mathématiciens locaux et ceux du continent se sont éloignés et le développement du calcul a été presque entièrement produit dans la ligne de Leibniz.

De nouvelles voies et bases solides

La diffusion du calcul a été très agile grâce aux revues de création récente. Ce n'est que dans la revue "Acta Eruditorum" qu'il y a plus d'une centaine d'articles à Leibniz du premier au vingt-cinq ans suivants, la plupart écrits par Leibniz lui-même et les frères Bernouilli. XVIII. Au XVIIIe siècle, le Calcul atteindrait le sommet avec de nombreuses méthodes et applications, dans lesquelles le nom d'Euler doit se situer bien au-dessus de ses contemporains. À côté de lui se détachent la deuxième génération de bernouillitos, D'Alembert et, plus tard, Lagrange.

Mais le Calcule avait un péché originel et l'évêque anglais Berkeley l'a dénoncé durement en 1735, dans son livre " The Analyst ": les derniers rapports des quantités dévastatrices de Newton qui étaient mentionnés à la base du raisonnement " et les "infinitésimaux" de Leibniz étaient inacceptables par la reine. Dans les mots de Berkeley: "Ce qui peut avaler le deuxième ou troisième flux et le deuxième ou troisième différentiel ne devrait pas se soucier, à mon avis, des problèmes de la Divinité », c'est à dire, l'un et l'autre sont des questions de foi. Oui, il ne conteste pas les résultats obtenus.

Bien que cent ans plus tôt Cavalieri avait écrit "l'erreur est un problème des philosophes et non des mathématiciens", les mathématiciens qui ont essayé de construire le calcul sur des bases solides, il est remarquable l'importance donnée par D'Alembert au concept de limite pour la "Encyclopedie". XIX. Au début du XXe siècle Bolzano, Prague et Cauchy, ont donné une définition adéquate de la limite à Paris (équivalent à celui qui existe dans n'importe quel livre d'aujourd'hui) et à partir de lui est définie la dérivée.

L'intégrale, avec Cauchy, est passée de l'inverse de la dérivée à la définir par une limite et a ensuite dû démontrer l'inverse entre les deux. L'Intégrale a suivi son propre chemin et a créé la soi-disant Théorie de la Mesure; Lebesgue XX. Ce qui a pris fin au début du XXe siècle. En plus de la définition générale de l'intégrale, il a réussi le théorème de différenciation, la formulation moderne du théorème de Newton-Leibniz.