"Principia" 300 anys (2) Isaac Newton, creador del càlcul

1987/04/01 Duoandikoetxea Zuazo, Javier - EHUko matematika irakaslea Iturria: Elhuyar aldizkaria

• Fisika

Caminant

La Matemàtica grega, basada en gran manera en la Geometria, sembla normal que es vulgui calcular la superfície de les figures planes i el volum dels sòlids. De la mateixa manera, en fer els primers passos de la Física van mostrar interès per aconseguir un centre de gravetat. La major part d'aquests problemes es deuen a Arquimedes, un servent (a. C.). III. En el segle XIX): superfícies d'el·lipses i segments parabòlics, volum de molts sòlids de revolució (esfera, el·lipsoide, segment de paraboloides, etc.) i el centre de gravetat de la majoria, per exemple.

Però Arquimedes no tenia la formulació fàcil que ofereix el Càlcul actual (la integral d'una sola funció dóna lloc a diverses resulsiones d'Arquimedes) i cada problema era nou per a ell. Per a l'obtenció dels resultats es va valer de la seva intuïció geomètrica, descomponent sovint la imatge en fragments molt petits i aproximant aquests per figures conegudes (triangles, quadrats, cilindres). Posteriorment, per a justificar-ho, utilitzava el "mètode exhacutivo" adoptat per Eudel.

Aviat les Matemàtiques (almenys les relacionades amb el càlcul) van quedar adormides i amb ella els treballs d'Arquimedes. Els àrabs van portar aquestes obres a l'oest d'Europa, on va ser el XVI. En el segle XX van reprendre el seu estudi. XVII. Es pot dir que a principis del segle XX s'entenien les obres d'Arquimedes, almenys prou per a donar nous fruits. En aquests cinquanta anys fins a arribar a Newton es van acumular noms i rescatats: Kepler, Cavalieri, Torricelli, Roberval, Descartes, Fermat, Pascal, Wallis, Barrow, etc.

De la mà de Descartes, la Geometria Analítica va tenir una gran influència en el Càlcul, ja que l'expressió algebraica de les corbes va provocar una nova i àgil formulació de problemes. Un pas important va ser el de la classificació de problemes, amb dos grans grups: els problemes de tangents i els problemes de superfícies, que els reben dels models principals. Els problemes del primer grup (rectificar una corba en un punt o calcular els màxims i mínims) eren pràcticament nous, ja que en les Matemàtiques antigues no apareixen i es resolen mitjançant la derivada. Els del segon grup, no obstant això, són formulats per Arquimedes i avui els associem a la integració.

Entre els matemàtics a dalt esmentats, Fermat va ser el més avançat en la resolució d'aquests problemes. Per al càlcul de màxims i mínims, per exemple, va donar el següent mètode: Trobar el valor A per al qual [F(A + E) - F (A)] / E = 0, fent E = 0 (una vegada obtingut el quocient). Encara que sembli un derivat, aquí no hi ha límit, ja que Fermat ho fa per a polinomis, on el quocient és sempre exacte. En integració, avui

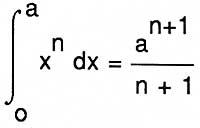
coneixia l'equivalent geomètric de la fórmula, una cosa demostrada en Cavalieri, Pascal o Roberval.

I va arribar Newton

El jove Newton va conèixer i aviat va dominar les tècniques dels llibres de Matemàtiques llegint el seu propi llibre. Aquesta formació autodidàctica no és sorprenent, tenint en compte que en les Universitats no s'impartien cursos ordinaris sobre aquest tema. En tot cas, comptaria amb la col·laboració de Barrow, tant en la selecció de llibres com en el curs que aquest va impartir durant un any. No obstant això, és conegut que van passar de la mà de Newton de llavors i que va tenir una gran influència de dues: La Geometria de Descartes i la dels llibres "Arithmetica Infinitorum" de Wallis.

Però Newton es va avançar a tots en 1665-66 anys, ja que fins llavors havia vist com ningú la clau dels problemes i la solució era donar una regla per a fer la derivada, demostrar que la integral era la inversa de la derivada i indicar la via d'aplicació en diferents problemes.

Newton mesurava totes les quantitats variables respecte al temps (més tard va dir que el temps és qualsevol quantitat que canvia uniformement): eren fluentes. Les velocitats de canvi es denominaven fluxos. Una corba laun és deguda al moviment de l'abscissa i l'ordenada i tant x com i tenen els seus fluxos x e i. Donada l'equació de la corba, es busca la relació entre els fluxos. Com ho aconseguirà? Substituir x e i per x + x o e i + i o en l'equació de la corba per a escurçar la inicial, dividir per o i fer 0 aquesta o. El mètode, a més de l'estil, és l'actual, amb la possibilitat de realitzar una derivada implícita.

Per exemple, per a derivar i = x m/n, aplica el seu mètode a la relació yn = xm: Després de tractar tots dos costats de la igualtat (i + i o ) n = (x + x o ) m amb la fórmula del binomi, després de dividir i n i x m eliminats per o, i anul·lar aquest o, obté n i n-1 i = m x m-1 x. N'hi ha prou amb substituir i per x m/n,

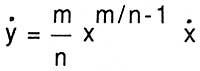
per a tenir una derivada coneguda.

El teorema bàsic del càlcul o la inversa de la integració i la derivació, va ser formulat geomètricament per Barrow en el llibre " Lectiones Geometricae" (publicat en 1670), però no sembla que s'apropiés del seu valor. "La fórmula de Newton-Leibniz" és la seva presentació més senzilla: Si F' = f,

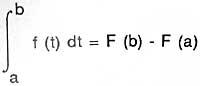
o bé,

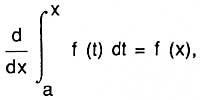
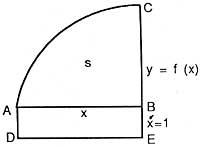
és a dir, la derivada de l'abscissa de la superfície és funció (o ordenada). Vegem la formulació de Newton. Biz i = f (x) corba i s = superfície (ABC) (veure figura), que es genera pel moviment paral·lel de la recta vertical BC. Biz x = AB i fem el paral·lelogram ABED considerant AD = 1. Llavors x = superfície (ABDE), aquesta superfície és generada pel moviment de la VEU. La relació de velocitats d'increment de totes dues superfícies, segons Newton, és igual a la relació BC i BE, és a dir, s/x = BC/BE = f(x).

Una vegada decidit això, en ser més fàcil derivar, la taula d'integrals contindrà les derivades a l'inrevés. D'aquesta manera, no obstant això, moltes corbes encara no poden integrar-se i seguint una idea presa de Wallis per a ampliar les possibilitats, va considerar els desenvolupaments seriats de les funcions i els va seguir per a aconseguir una nova sèrie de temes integrats (sense fer cas als problemes de convergència, per descomptat).

L'expansió de (1 + x) m, quan m és total, encara que es diu binomi de Newton, resulta realment interessant quan m és incomplet, llavors el polinomi no és una sèrie infinita. m enmig de dos nombres enters (1/2, 3/2, ...) ja es deu a Newton la resposta del cas, ja que va demostrar que s'aplica la mateixa regla que els coeficients dels polinomis per als coeficients.

Amb l'objectiu de basar-se en el que s'estava fent, Newton farà referència a les relacions dels increments: flux " la primera relació dels increments emergents " o " l'última relació dels increments fungibles ". A la vista de la imatge, suposem que avancem una mica l'abscissa, llavors la superfície augmenta i cal aconseguir una relació entre els increments de superfície i abscissa, però la primera relació flueix és ", abans de començar a moure's ... Així mateix, considerant el procés cap endarrere, els increments desapareixen i l'última relació d'increments destructius " és el flux. Es pot suscitar la idea de límit indeterminat.

Cal compartir els honors

Entre les obres de Newton, les relacionades amb el Càlcul són: "D'Analysi per Aequationes Numero Terminorum Infinites" (escrit cap a 1669, publicat en 1711), " Methodus Fluxionum et Serierum Infinitorum" (escrit en 1671, publicat en 1736), " Tractatus de Quadratura Curvarum" (escrit en 1693, pàgines 1704) i "principi" (pàg. Com es veu, van passar vint anys entre l'obtenció dels rescatats i el seu acomiadament, i així, en 1675, Leibniz va arribar per la seva part a semblances. El primer article de Leibniz es va publicar en 1684, anticipant-se durant tres anys a Principia "".

En 1698 Fatio de Duillier, amic de Newton, va publicar un llibre en el qual li va reconèixer tot el mèrit denunciant que Leibniz havia fet plagi. Leibniz es va defensar a si mateix i van passar deu anys fins que el segon atac va arribar en un article de Keill. Aquest article va sortir en la revista de la Reial Societat i Leibniz, com a associat, va sol·licitar en 1711 al secretari que aclarís el problema.

Quan el president era Newton, es va nomenar un comitè i la decisió de la comissió va ser encara més dura per a Leibniz. A més, van decidir publicar la col·lecció de cartes "Commercium Epistolicum" contra Leibniz. El debat es va engrandir i algunes persones de Leibniz es van adonar d'alguns errors de Newton. Leibniz, en 1714, va escriure el programa " Història et origo Calculi differentialis " per a comptar la seva veritat. Malgrat la seva mort dos anys després, Newton va continuar atacant.

XX. Fins al segle XIX aquest punt ha estat sense decidir, però quan s'han analitzat els manuscrits de Leibniz se l'ha reconegut definitivament el seu mèrit i avui a tots dos els correspon l'honor de ser creadors del Càlcul. El debat, no obstant això, va afectar més a Anglaterra, on els matemàtics locals i els del continent es van allunyar i el desenvolupament del Càlcul es va produir gairebé íntegrament en la línia de Leibniz.

Nous camins i bases sòlides

La difusió del càlcul va resultar molt àgil gràcies a les revistes de recent creació. Només en la revista "Acta Eruditorum" hi ha més d'un centenar d'articles en Leibniz des del primer fins als vint-i-cinc anys següents, la majoria escrits pel propi Leibniz i els germans Bernouilli. XVIII. En el segle XVIII el Càlcul arribaria al cim amb nombrosos mètodes i aplicacions, en els quals el nom d'Euler ha de situar-se molt per sobre dels seus contemporanis. Al costat d'ell destaquen la segona generació de bernouillitos, D'Alembert i, més tard, Lagrange.

Però el Calculo tenia un pecat original i el bisbe anglès Berkeley ho va denunciar amb duresa en 1735, en el seu llibre " The Analyst ": les últimes relacions de les quantitats devastadores de Newton que s'esmentaven en la base del raonament " i els "infinitesimals" de Leibniz eren inacceptables per part de la reina. En paraules de Berkeley: "El que pot engolir el segon o tercer flux i el segon o tercer diferencial no hauria de preocupar-se, al meu entendre, dels problemes de la Divinitat ", és a dir, l'un i l'altre són qüestions de fe. Això sí, no qüestiona els resultats obtinguts.

A pesar que cent anys abans Cavalieri havia escrit "l'error és un problema dels filòsofs i no dels matemàtics", els matemàtics que van tractar de construir el Càlcul en bases sòlides, és destacable la importància donada per D'Alembert al concepte de limiti per a l'Encyclopedie "". XIX. A principis del segle XX Bozen, Praga i Cauchy, van donar una definició adequada del límit a París (equivalent al que existeix en qualsevol llibre d'avui) i a partir d'ell es defineix la derivada.

La integral, amb Cauchy, va passar de ser la inversa de la derivada a definir-la mitjançant un limiti i llavors va haver de demostrar la inversa entre ambdues. La Integral va seguir el seu propi camí i va crear l'anomenada Teoria de la Mesura; Lebesgue XX. El que va acabar a principis del segle XX. A més de la definició general de la integral, va aconseguir el teorema de diferenciació, la formulació moderna del teorema de Newton-Leibniz.