NAVIER-STOKES: caught in the whirlpool of questions

2021/07/05 Gontzal Lopez Ruiz - Ingeniaritza fisikoan doktoregaiaIkerlan-EHU Iturria: Elhuyar aldizkaria

• Matematika

Friction, origin of headaches

Blood flow through the arteries of the heart, movement of currents and clouds of atmospheric air, or flow around the blades of an airplane: we can form an endless list of physical phenomena related to fluid dynamics. From the hand of the great names of physics and mathematics, throughout history there have been numerous efforts to understand and foresee these phenomena. As we could expect, we must go to the domain of lights to find the first sketches of differential equations that describe the dynamics of “ideal” fluids. In particular, in 1755 Leonhard Euler presented the differential equation of the “ideal fluids”, assuming that the friction between the fluid particles against the inertia forces was negligible, as in waterfalls and, in general, in high-speed flows.

Although it was a breakthrough, for example, to calculate the slow motion of honey, the Euler equation fails, since the viscosity of the flow (the friction forces) is more important against inertial forces. The same problem occurs in the resolution of flows in relation to solids or obstacles, since near the obstacle large speed gradients are generated due to friction forces. Faced with this, in 1822 Claude-Louis Henri Navier and twenty years later George Gabriel Stokes added to Euler's equation the influence of friction of viscous or viscous fluid, formulating what we know today as Navier-Stokes equations. Below are two basic principles applied to a particle of fluids: the conservation of mass (continuity equation) and Newton's second law, which relates the rate of growth of the moment of the fluid particle (to the left of the equation) to the forces of pressure, gravity and friction that cause it (to the right of the equation).

In the darkest corners of mathematics

As usual, to reach the solution of differential equations it is necessary to establish initial conditions. In this case, we must provide the Navier-Stokes equations (an equation in each direction) with a flow velocity and pressure distribution in the three dimensions of space at a given time. From there, the equations should return the speed and pressure of the flow at any time in the future. What would this mean? For example, we would be able to accurately predict weather phenomena over time, to fully define the movement of ocean currents and waves, to precisely solve aerodynamics around bodies… If this were possible, we would probably see and understand reality differently. Unfortunately, after two centuries, the analytical solution is only known for those flows that meet certain conditions. Just look at the cause equation: partial derivatives of the second order (in friction forces) and nonlinearity (in convective acceleration) present enormous difficulties in analytically solving the equations.

Even if it seems a lie, from the point of view of physicists and engineers, equations can describe reality with complete reliability, how is it possible? To do this, a common mathematical tool is used: solving equations by numerical methods, writing each term of the equation algebraically and applying certain boundary conditions, obtaining approximate solutions.

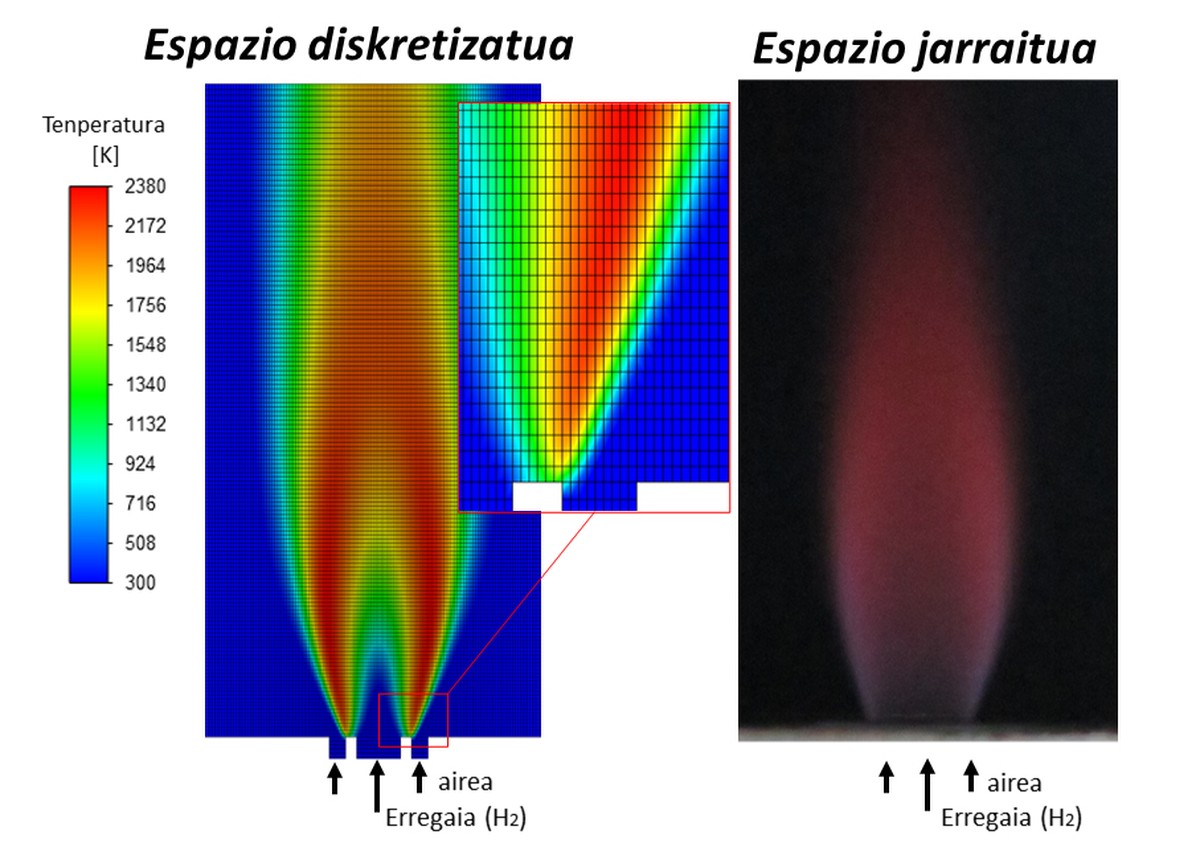
The discipline known as “Computational Fluid Dynamics” or CFD, resolves the Navier-Stokes equations through matrix algebra in lamine and turbulent flows. Although the cost of computational calculation can be very high depending on the problem, in recent decades this simulation tool has gained strength in various fields of research and industry. In fact, fluid movement can be accompanied by simulation of heat transfer, chemical reactions or deformation of solids produced by fluids, solving multi-physical problems that occur in reality. In art, mathematicians work to demonstrate the existence and loneliness of solutions.

Out of reality?

In 1933, the mathematician Jean Leray demonstrated the existence and solitude of the “weak” solutions of the equations considering a small interval of time [3]. Yes, as you can see, it greatly simplified the problem. Faced with soft solutions, through a weak formulation can be found non-differential solutions that can present the equation, facilitating as a starting point the learning of the existence and loneliness of the equations. This important antecedent has led mathematicians to adopt a new position in the face of the problem, according to Tristan Buckmaster of Princeton University, “one of the strategies would be to demonstrate that Leray’s weak solutions are soft, and if it were achieved would solve the problem of the millennium” [2]. Soft solutions would completely describe physical reality, having a solution at each point in the area considered at any time (solutions of speed and pressure zones). The key and main doubt of mathematicians is that by starting the calculation considering a gentle formulation, suitable velocity vectors can be obtained over time, but it is possible that suddenly the results return infinite velocity at some point in the field: the equations have exploded.

In this sense, recent advances have intensified their doubts. In the article published in 2017 by mathematicians Tristan Buckmaster and Vlad Vicol of Princeton University [4], for certain definitions of “weak” solutions, the solitude of Leray’s solutions was questioned. These results allow, from initial conditions, to reach physically impossible situations. However, doubts are raised about the results raised in the article; solutions considered “weak” may affect the final result and there may be a loneliness for “less weak” solutions.

Need for drills

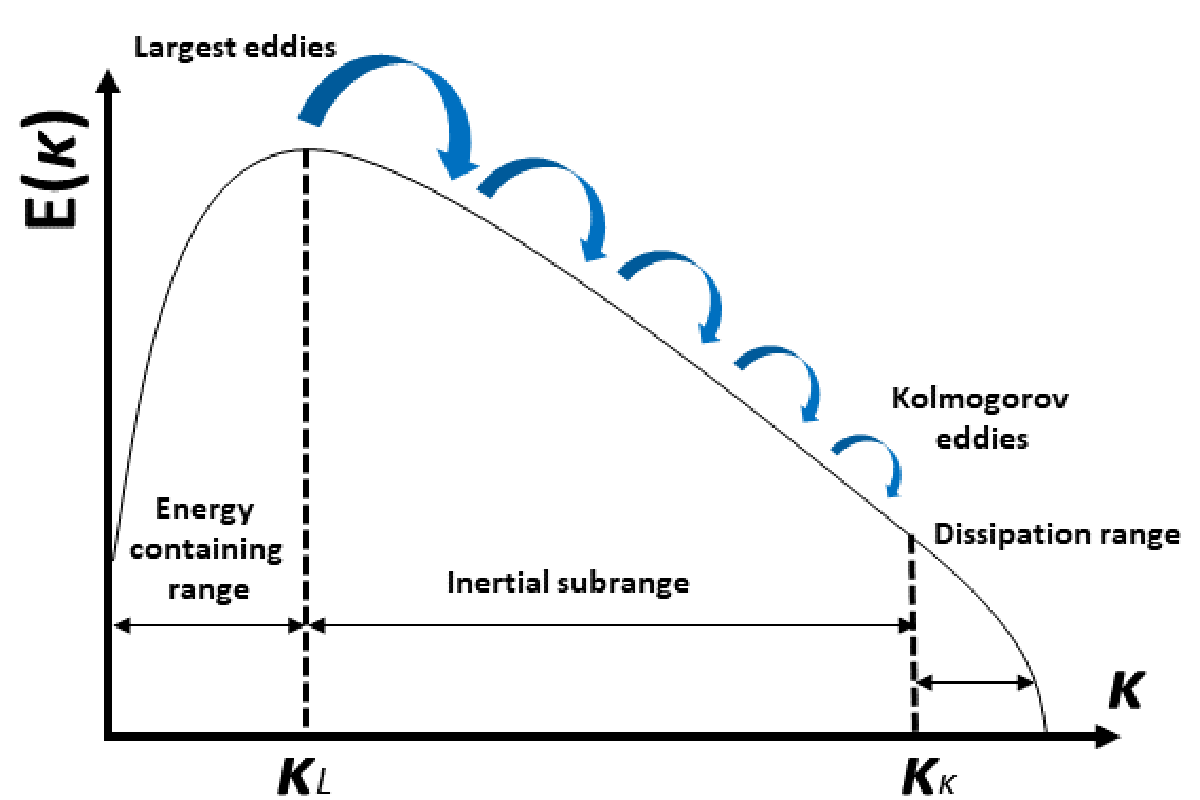
As mentioned, the numerical methods and algorithms developed in recent decades allow us to approximate the Navier-stokes equations. However, within the CFD calculations there are a number of problems whose main challenge is the development of suitable physical models to simulate turbulent flow along with other phenomena (combustion reactions, deformations of objects, heat transfer). The main characteristic of turbulent flows is the chaotic and disordered motion of particles, formed by turbulence at different scales. Therefore, the trajectories of fluid particles suffer over time strong changes of direction and speed, making it difficult to calculate by numerical methods. To understand the relationship of whirlpools to different sizes or scales, the spectrum or scale of turbulent kinetic energy was defined [5]. According to this scale, large eddies transmit kinetic energy across the spectrum to the smaller turbulent of similar size, reaching small scales and until the viscosity of the fluid dissipates the eddies. It can be said that the spectrum shows us the competition between inertia and friction forces.

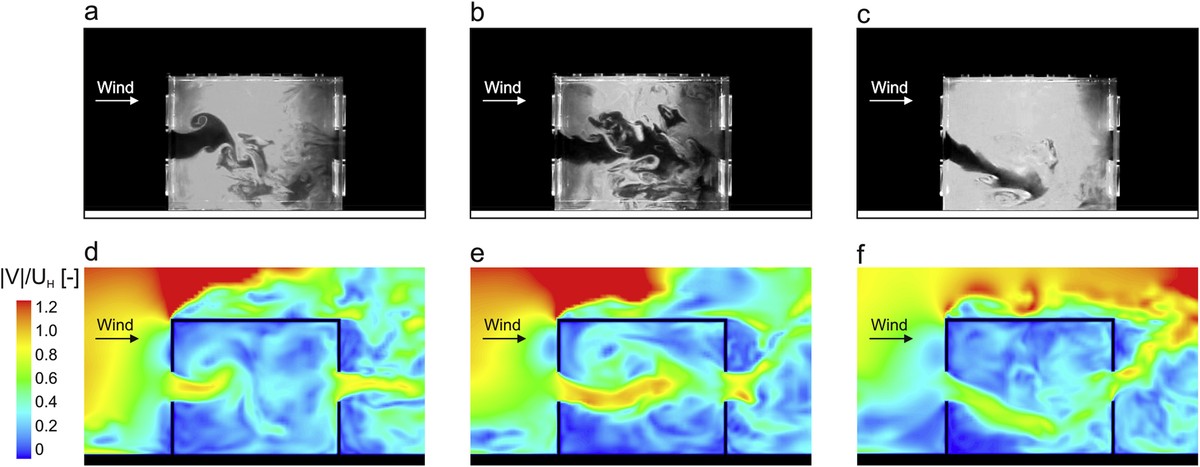
Based on this concept different models have been developed depending on the size of whirlwind that is intended to be solved. For example, solving the entire scale by numerical methods at the points of the space considered (known as Direct Navier-Stokes or DNS) is a luxury within the reach of a few, since to solve the times and spaces so small in the smaller turbulence it is necessary to use calculations by super-computer. In order to reduce computational cost, the most common turbulent models establish filters at scale, solving one part (high turbulence) and modeling another (minor turbulence). In recent years this technique, known as Large Eddy Simulation or LES, has gained strength in the research of physical problems and in the development of designs aimed at different sectors.

Although we hope to resolve reality through these equations, we must not forget that differential equations are human-generated approaches. The Clay Mathematics Institute award will have to wait for the continued work of mathematicians to yield clear results. In addition, in order to reduce computational cost and improve the accuracy of approximate solutions using numerical methods, researchers work in this field of developing science. The phrase put in the mouth of physicist Werner Heisenberg summarizes well the magnitude of the challenge: “When I meet God I will ask you two questions: Why relativity? And why the turbulence? I am sure you will have an answer to the first question.”

 

BIBLIOGRAPHY:

[1] Fefferman C. 2006. “Existence and smoothness of the Navier-Stokes equation”, Millennium Prize Problems, Clay Math. Inst., Cambridge, MA, 2006, 57-67, URL: https://www.claymath.org/sites/default/files/navierstokes.pdf

2] K. Hartnett 2017 Mathematicians Find Wrinkle in Famed Fluid Equations. Quantamagazine. URL: https://www.quantamagazine.org/mathematicians-find-wrinkle-in-famed-fluid-equations-20171221/

[3] Leray J. 1934. “Sur le mouvement d’un liquide visqueux emplissant l’espace”. Minutes Math., 63(1), 193–248.

[4] Buckmaster T. and Vicol V. 2019. “Nonuniqual of weak solutions to the Navier-Stokes equation”. Ann. of Math. (2) 189 (2019), no. 1, 101–144.

[5] Kolmogorov A.N. 1941. “Dissipation of energy in locally isotropic turbulence”. Doc. Acad. Nau. SSSR, 32, 16-18.

[6] van Hooff T., B. de Block and Tominaga Y. 2017 “On the accuracy of CFD simulations of cross-ventilation flows for a generic isolated building: Comparison of RANS, LES and experiments”. Building and Environment, 114, 148-165.