NAVIER-STOKES: atrapat en el remolí de preguntes

Equació de Navier-Stokes (a dalt). Dos exemples de la importància de les forces d'inèrcia i fricció són els salts d'aigua i el flux de mel respectivament (a baix). Ed. Go

Fricció, origen dels maldecaps

Flux sanguini a través de les artèries del cor, moviment dels corrents i núvols d'aire atmosfèric, o flux al voltant de les aspes d'un avió: podem formar una llista interminable de fenòmens físics relacionats amb la dinàmica dels fluids. De la mà dels grans noms de la física i les matemàtiques, al llarg de la història han estat nombrosos els esforços per comprendre i preveure aquests fenòmens. Com podíem esperar, hem d'anar al domini de les llums per a trobar els primers esbossos de les equacions diferencials que descriuen la dinàmica dels fluids “ideals”. En concret, en 1755 Leonhard Euler va presentar l'equació diferencial dels “fluids ideals”, suposant que la fricció entre les partícules de fluid enfront de les forces d'inèrcia era menyspreable, com en salts d'aigua i, en general, en els fluxos d'alta velocitat.

Encara que va ser un gran avanç, per exemple, per a calcular el moviment lent de la mel, l'equació d'Euler falla, ja que la viscositat del flux (les forces de fricció) té més importància enfront de les forces inercials. El mateix problema es produeix en la resolució dels fluxos en relació amb els sòlids o obstacles, ja que prop de l'obstacle es generen grans gradients de velocitat a causa de les forces de fricció. Enfront d'això, en 1822 Claude-Louis Henri Navier i vint anys després George Gabriel Stokes van afegir a l'equació d'Euler la influència del fregament del fluid viscós o viscós, formulant el que avui coneixem com a equacions de Navier-Stokes. A continuació es troben dos principis bàsics aplicats a una partícula de fluids: la conservació de la massa (equació de continuïtat) i la segona llei de Newton, que relaciona la taxa de creixement del moment de la partícula del fluid (a l'esquerra de l'equació) amb les forces de pressió, gravetat i fricció que el provoquen (a la dreta de l'equació).

En els racons més foscos de les matemàtiques

Com és habitual, per a arribar a la solució d'equacions diferencials és necessari establir condicions inicials. En aquest cas, hem de proporcionar a les equacions de Navier-Stokes (una equació en cada direcció) una distribució de velocitat i pressió del flux en les tres dimensions de l'espai en un moment donat. A partir d'aquí, les equacions haurien de retornar la velocitat i la pressió del flux en qualsevol moment del futur. Què suposaria això? Per exemple, seríem capaços de predir exactament els fenòmens meteorològics al llarg del temps, de definir completament el moviment dels corrents oceànics i de les ones, de resoldre amb precisió l'aerodinàmica entorn dels cossos… Si això fos possible, probablement, veuríem i entendríem la realitat d'una altra manera. Lamentablement, transcorreguts dos segles, la solució analítica només es coneix per a aquells fluxos que compleixen certes condicions. N'hi ha prou amb fixar-se en l'equació de la causa: les derivades parcials de segon ordre (en les forces de fregament) i les no linealitats (en l'acceleració convectiva) presenten enormes dificultats a l'hora de resoldre analíticament les equacions.

Encara que sembli mentida, des del punt de vista de físics i enginyers, les equacions poden descriure la realitat amb total fiabilitat, com és possible? Per a això s'utilitza una eina matemàtica habitual: resoldre equacions mitjançant mètodes numèrics, escrivint cada terme de l'equació de manera algebraica i aplicant determinades condicions de contorn, obtenint solucions aproximades.

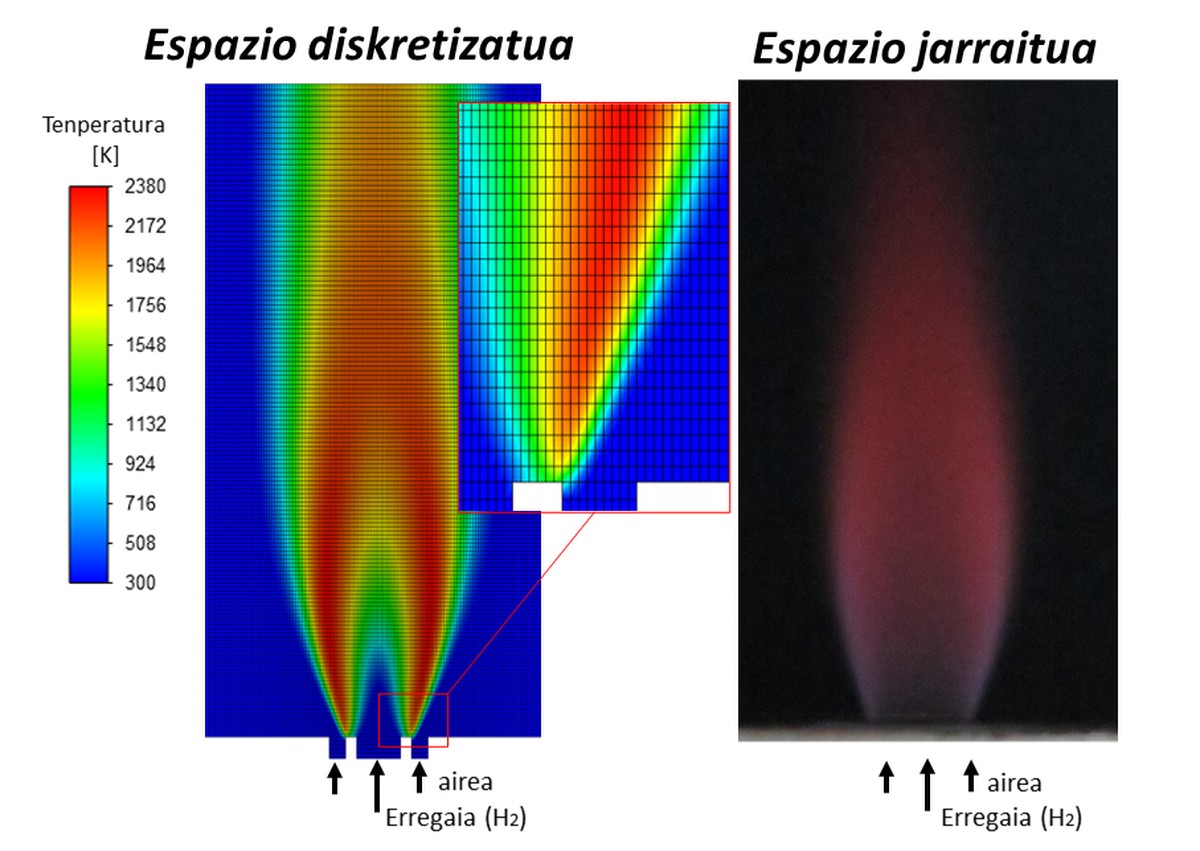
La disciplina coneguda com “Computational Fluïu Dynamics” o CFD, resol les equacions de Navier-Stokes a través de l'àlgebra de matrius en els fluxos laminos i turbulents. A pesar que el cost del càlcul computacional pot ser molt elevat en funció del problema plantejat, en les últimes dècades aquesta eina de simulació ha cobrat força en diversos àmbits de la recerca i la indústria. De fet, el moviment dels fluids pot anar acompanyat de la simulació de la transferència de calor, les reaccions químiques o les deformacions dels sòlids produïts pels fluids, resolent problemes multi-físics que es donen en la realitat. En l'art, els matemàtics treballen per a demostrar l'existència i la solitud de les solucions.

Fora de la realitat?

En 1933, el matemàtic Jean Leray va demostrar l'existència i solitud de les solucions “febles” de les equacions considerant un petit interval de temps [3]. Sí, com es pot veure, va simplificar molt el problema. Enfront de solucions suaus, mitjançant una formulació feble es poden trobar solucions no diferencials que poden presentar l'equació, facilitant com a punt de partida l'aprenentatge de l'existència i la solitud de les equacions. Aquest important antecedent ha portat als matemàtics a adoptar una nova posició davant el problema, segons Tristan Buckmaster, de la Universitat Princeton, “una de les estratègies seria demostrar que les solucions febles de Leray són suaus, i si s'aconseguís resoldria el problema del mil·lenni” [2]. Solucions suaus descriurien completament la realitat física, disposant d'una solució en cadascun dels punts de l'àrea considerats en qualsevol moment (solucions de zones de velocitat i pressió). La clau i el principal dubte dels matemàtics és que en posar en marxa el càlcul considerant una formulació suau, es poden obtenir vectors de velocitat adequats al llarg del temps, però és possible que de sobte els resultats retornin la velocitat infinita en algun punt del camp: les equacions han fet explotar.

En aquest sentit, els últims avanços han intensificat els seus dubtes. En l'article publicat en 2017 pels matemàtics Tristan Buckmaster i Vlad Vicol de la Universitat de Princeton [4], per a certes definicions de solucions “febles”, es va qüestionar la solitud de les solucions de Leray. Aquests resultats permeten, a partir d'unes condicions inicials, arribar a situacions físicament impossibles. No obstant això, es plantegen dubtes sobre els resultats plantejats en l'article; és possible que les solucions considerades “febles” incideixin en el resultat final i existeixi una solitud per a les solucions “menys febles”.

Necessitat de simulacres

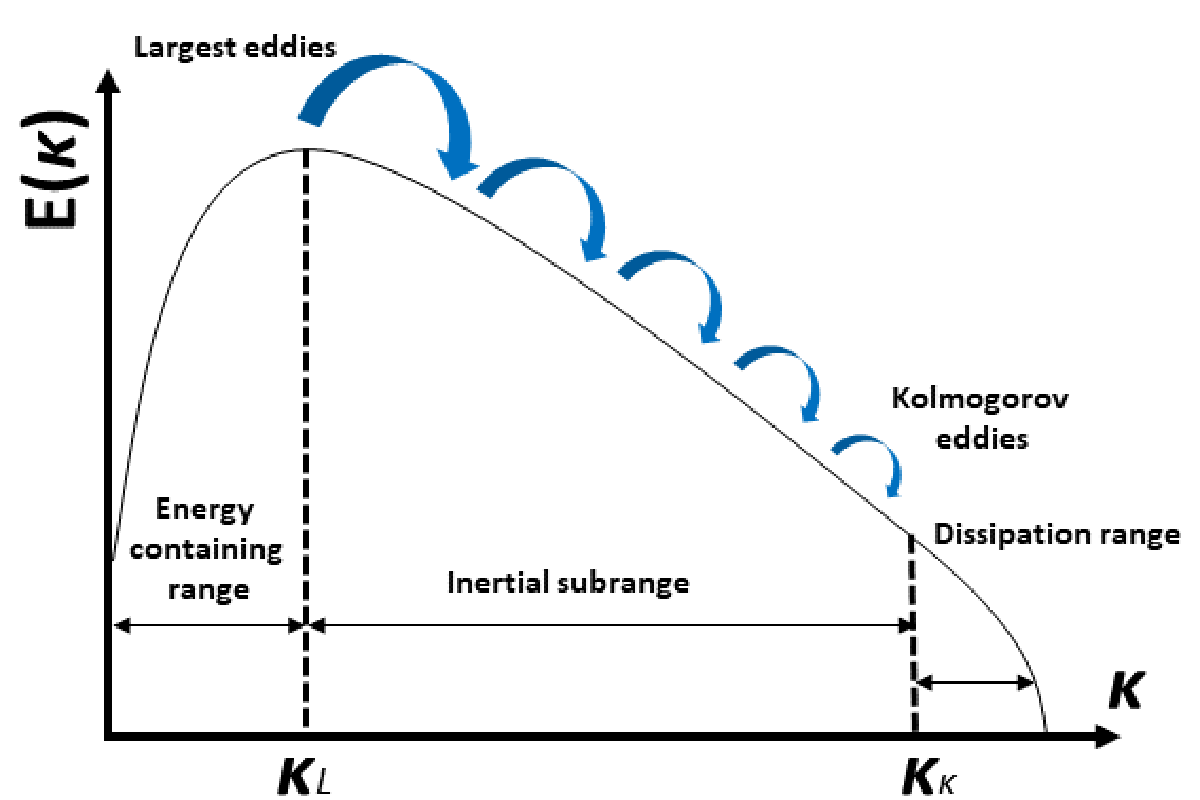
Com s'ha comentat, els mètodes numèrics i algorismes desenvolupats en les últimes dècades permeten resoldre de forma aproximada les equacions de Navier-stokes. No obstant això, dins dels càlculs CFD existeixen una sèrie de problemes el principal repte dels quals és el desenvolupament de models físics adequats per a simular el flux turbulent juntament amb altres fenòmens (reaccions de combustió, deformacions d'objectes, transferència de calor). La característica principal dels fluxos turbulents és el moviment caòtic i desordenat de les partícules, format per turbulències a diferents escales. Per tant, les trajectòries de les partícules de fluid sofreixen al llarg del temps forts canvis de direcció i velocitat, dificultant el càlcul per mètodes numèrics. Per a comprendre la relació de remolins a diferents grandàries o escales es va definir l'espectre o escala d'energia cinètica turbulenta [5]. Segons aquesta escala, els remolins grans transmeten energia cinètica a través de l'espectre als turbulents menors de grandària similar, arribant a escales petites i fins que la viscositat del fluid dissipa els remolins. Es pot dir que l'espectre ens mostra la competència entre les forces d'inèrcia i fricció.

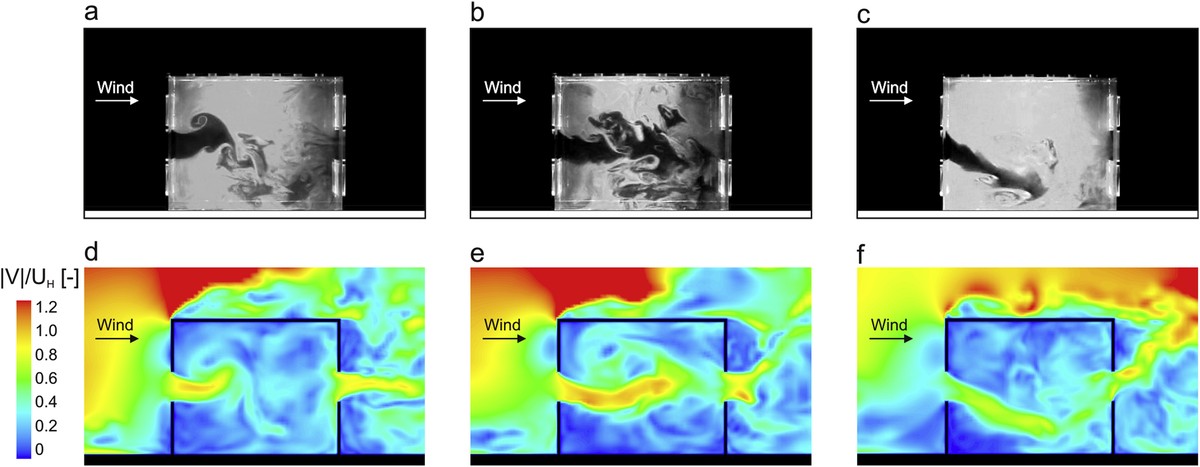
Sobre la base d'aquest concepte s'han desenvolupat diferents models en funció de la grandària de remolí que es pretén resoldre. Per exemple, resoldre tota l'escala mitjançant mètodes numèrics en els punts de l'espai considerat (conegut com Direct Navier-Stokes o DNS) és un luxe a l'abast d'uns pocs, ja que per a resoldre els temps i espais tan petits en les turbulències més petites és necessari utilitzar càlculs per super-computador. Amb la finalitat de reduir el cost computacional, els models turbulents més habituals estableixen filtres a escala, resolent una part (turbulents elevats) i modelant una altra (turbulències menors). En els últims anys aquesta tècnica, coneguda com Large Eddy Simulation o ELS, ha pres força en la recerca de problemes físics i en el desenvolupament de dissenys dirigits a diferents sectors.

Encara que esperem resoldre la realitat a través d'aquestes equacions, no hem d'oblidar que les equacions diferencials són aproximacions generades per l'home. El premi de l'Institut de Matemàtiques Clay haurà d'esperar que el treball continu dels matemàtics doni resultats clars. A més, amb l'objectiu de reduir el cost computacional i millorar la precisió de solucions aproximades mitjançant mètodes numèrics, els investigadors treballen en aquest camp de la ciència en desenvolupament. La frase que posen en boca del físic Werner Heisenberg resumeix bé la magnitud del repte: “Quan em trobo amb Déu li faré dues preguntes: Per què la relativitat? I per què la turbulència? Estic segur que tindrà resposta a la primera pregunta”.

 

BIBLIOGRAFIA:

[1] Fefferman C. 2006. “Existence and smoothness of the Navier-Stokes equation”, Millennium Prize Problems, Clay Math. Inst., Cambridge, DT., 2006, 57-67, URL: https://www.claymath.org/sites/default/files/navierstokes.pdf

2] K. Hartnett 2017 Mathematicians Find Wrinkle in Famed Fluïu Equations. Quantamagazine. URL: https://www.quantamagazine.org/mathematicians-find-wrinkle-in-famed-fluid-equations-20171221/

[3] Leray J. 1934. “Sud le mouvement d’un liquidi visqueux emplissant l’espace”. Acta Math., 63(1), 193–248.

[4] Buckmaster T. i Vicol V. 2019. “Nonuniqual of weak solutions to the Navier-Stokes equation”. Ann. of Math. (2) 189 (2019), no. 1, 101–144.

[5] Kolmogorov A.N. 1941. “Dissipation of energy in locally isotropic turbulence”. Doc. Acad. Nau. SSSR, 32, 16-18.

[6] van Hooff T., B. de Block i Tominaga I. 2017 “On the accuracy of CFD simulations of cross-ventilation flows for a generic isolated building: Comparison of RANS, ELS and experiments”. Building and Environment, 114, 148-165.