Claude Shannon, père du monde numérique
2016/09/01 Leturia Azkarate, Igor - Informatikaria eta ikertzailea Iturria: Elhuyar aldizkaria

Interrogé par les personnes les plus importantes dans le monde des technologies de l'information et de la communication, la plupart des gens ne seront probablement pas en mesure de donner des noms au-delà de Bill Gates, Steve Jobs, etc. Ceux qui connaissent le mieux le monde de l'informatique diraient sûrement d'autres noms comme Alan Turing ou Tim Berners-Lee. Parmi nous peut-être pas tellement mentionneraient Claude Shannon. Nous ne savons pas quelle est la raison, mais Shannon n'a pas du tout la réputation que méritent ses immenses contributions; Shannon, par exemple, sera le nom le plus important du monde des TIC.
Claude Elwood est né le 30 avril 1916 dans un petit village de l'État américain du Michigan. Depuis son enfance, il a enseigné à l'école la compétence en science et en mathématiques, ainsi que l'affection pour l'invention et la construction de dispositifs mécaniques et électriques. Ainsi, en 1932, à seulement 16 ans, il commence ses études universitaires à l'Université du Michigan, et en 1936 il termine ses études de mathématiques et d'ingénierie électrique. Puis, en 1936, il commence à suivre un master en génie électrique au prestigieux Massachusetts Institute of Technology ou MIT. Et en 1940, il a défendu la thèse de doctorat en mathématiques dans cette même institution.
Bases de l'électronique numérique
Cependant, la première de ses deux plus grandes contributions à la science a été réalisée avant la thèse, notamment dans le projet de master, à seulement 21 ans. Selon plusieurs experts, c'était la thèse de master la plus importante de l'histoire.
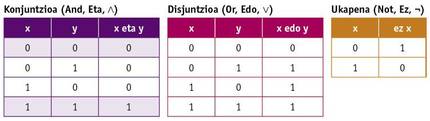
Pendant la réalisation du master, Shannon a pu travailler avec l'un des ordinateurs les plus puissants de l'époque, l'analyseur différentiel de Vannevar Bush. Ces ordinateurs étaient alors analogiques, fonctionnaient avec des poulies, des engrenages, etc. et ils occupaient un grand espace. Il a également eu la chance de connaître l'algèbre de Boole dans ses études de mathématiques. Dans l'algèbre de Boole les variables n'ont pas de valeur numérique mais Vérité et Mensonge (ou 0 et 1), et les opérations de base ne sont pas somme et multiplication, mais conjonction, disjonction et déni (And, Or et Not). Ces opérations sont définies par les tables de vérité suivantes:
Shannon a conçu dans le projet de master circuits électriques de commutateurs qui implémentaient l'algèbre de Boole. En outre, il a montré que les combinaisons de ces circuits permettaient de réaliser toute opération mathématique ou logique et a conçu certains d'entre eux. Ce travail a jeté les bases de la conception de circuits numériques, d'où l'électronique numérique. L'ordinateur et tous les autres appareils électroniques et numériques sont venus grâce à la vision qu'il a eue dans le projet de son master.
Théorie de l'information, base du stockage de l'information et de la communication numérique
Bien que cet apport soit vraiment impressionnant et surprenant, il est considéré comme son apport le plus important. Shannon est surtout connu pour la création d'un champ de connaissance de la théorie de l'information et pour son développement presque complet, en 1948, quand il travaillait dans des laboratoires prestigieux Bell, il a écrit dans son article “A mathematical theory of communication”.
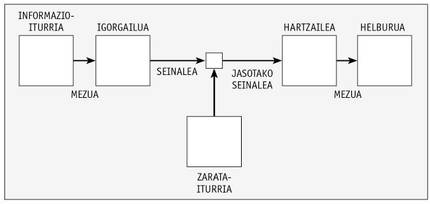
Dans cet article, Shannon a défini un système de communication à travers l'image ci-dessous.
Ainsi, il analyse et propose des moyens de coder le message de la manière la plus appropriée. L'image peut être appliquée de la même manière à un système de stockage dans lequel une information est écrite dans un milieu dans lequel le signal stocké en elle peut subir une dégradation et doit être la même que les informations écrites lors de la lecture.
Dans l'article, Shannon a proposé de convertir l'information en base binaire pour le stockage et le transport de l'information, c'est-à-dire par les nombres 0 et 1. Ces unités d'information ont été indiquées pour la première fois dans cet article binary digit ou bit, bien que le nom soit J. W. C'était la proposition de Tukey, compagnon de Shannon.
Convertir l'information en numérique était une avancée majeure. En fait, l'information analogique utilisée jusqu'à présent a plus de situations possibles (infinies en réalité), et puisque la différence d'une situation à l'autre est petite, tout bruit ou petit changement dans le stockage ou la transmission fait qu'un signal devient un autre et il est impossible de récupérer l'information exacte originale. Cela provoquait de grands problèmes dans la transmission des signaux, par exemple en soulevant périodiquement la puissance du signal avec des répéteurs, car une dégradation et une perte d'information irréparables se produisaient. Au contraire, en transférant l'information à la base binaire, il n'y a que deux situations possibles, 0 et 1, et la différence entre les deux peut être aussi grande que souhaité dans le signal physique (par exemple, 0 volts et 5 volts). Ainsi, même si le signal est légèrement dégradé ou modifié, il est plus difficile de convertir un 0 en 1 ou vice versa. Ainsi, les informations sont stockées de manière plus simple et plus fiable, et la transmission peut être effectuée aussi loin que vous le souhaitez par des répéteurs, sans perdre d'informations.
Cela, pour sa part, supposait une percée, mais Shannon est allé plus loin, définissant pratiquement toutes les techniques et formules mathématiques pour les méthodes actuelles de compression et de fiabilité dans le stockage et la communication.
Pour cela, il a défini plusieurs concepts. L'une d'elles est l'information qui émet un message. En fait, Shannon a dit que tous les messages ne donnent pas la même information: plus un message est probable parmi tous les possibles, moins l'information donne. En outre, parmi les symboles ou les caractères d'un message, un symbole plus fréquemment fournit moins d'informations. Pour mesurer l'information d'un symbole, il a donné la formule I =-log2 p, où p est la probabilité ou la fréquence du symbole. Cette mesure d'information indique également le nombre de bits nécessaires pour transmettre ce symbole. Ainsi, nous aurions besoin d'un bit pour indiquer chacun des deux résultats (lion ou kastillo) qui peuvent être obtenus en lançant une pièce, selon la formule. Ou pour représenter chacune des lettres d'un alphabet de 27 lettres, si tous avaient la même probabilité, 4,76 bits seraient nécessaires.
Il a également défini l'entropie d'un message. L'entropie du message est l'information moyenne qui contient un message, donc il est défini comme: H = Pi log2 pi. En outre, étant donné que certains symboles sont plus susceptibles dans des contextes que dans d'autres (dans le cas des lettres, par exemple, c'est qu'après la lettre q va u, ou qu'après les consonnes il est plus normal qu'une voyelle qu'une autre consonne), Shannon a également défini une entropie conditionnée dans laquelle on tient compte du signe précédent pour calculer les cotes. Eh bien, cette mesure de l'entropie nous dit à quel point un message peut être compressé sans perdre d'informations! Dans les messages de langage naturel, par exemple, compte tenu des fréquences des lettres et des fréquences conditionnées, l'entropie est inférieure à une, de sorte que chaque lettre peut être encodée en signaux de moins d'un bit. Et comment Shannon l'a fait. Les systèmes de compression sans perte (ZIP, RAR ou beaucoup d'autres qui sont utilisés dans les communications…) qui sont tellement utilisés aujourd'hui sont basés sur des formules et des méthodes de Shannon.
Peu avec cela, Shannon a également théorisé au sujet de la compression avec perte, et tous les systèmes qui utilisent ce type de compression (JPG, MP3, DivX…) l'ont fondamentalement.
Et si c'était peu, il a également écrit dans cet article sur les codes qui détectent et/ou corrigent des erreurs. Pour détecter d'éventuelles erreurs ou corriger des erreurs dans une information reçue ou lue, des informations supplémentaires redondantes sont envoyées. Exemple de ceci sont les numéros de contrôle dans les numéros de compte ou lettres qui ont ajouté au numéro de la carte d'identité espagnole. Ce sont, en définitive, les sommes de checksum ou de contrôle. Si nous avons échoué sur un certain nombre, la somme de contrôle ne correspond pas et nous saurons qu'il y a une erreur dans le nombre. Pour corriger l'erreur, nous devons vérifier manuellement car dans ces exemples, seul le code est utilisé pour détecter les erreurs.
Mais il est possible de compléter le message original même s'il y a des erreurs dans le message reçu. Pour cela, il est nécessaire d'entrer plus d'informations redondantes supplémentaires et, surtout, que tous les mots ou numéros possibles qui peuvent être envoyés dans le code ont une distance minimale entre eux. Ainsi, supposons que la distance entre tous les caractères possibles est de trois bits, si une erreur se produit dans un bit nous pouvons savoir avec une certitude suffisante quel était le caractère à envoyer, si la probabilité de recevoir deux bits erronés d'un signal est relativement faible. Ainsi, en fonction de la fiabilité du canal, nous effectuerons une distance plus ou moins longue entre les signaux du code (nombre de bits) et nous introduirons plus ou moins d'informations redondantes, mais le récepteur pourra également réparer les messages erronés.
Les codes qui corrigent des erreurs ne sont pas inventés par Shannon. Son compagnon Richard Hamming était le pionnier à ce sujet. Mais Shannon a formalisé mathématiquement la théorie des codes de correction d'erreurs et défini le nombre maximum de bits supplémentaires nécessaires pour différentes probabilités de défaillance du canal. Et cette formulation est celle qui utilise tous les codes capables aujourd'hui de corriger les erreurs, avec des milliers d'utilisations: dans les communications spatiales et autres, dans le stockage d'informations sur CD et clés USB, etc.
Comme vous le voyez, les contributions de Shannon dans l’article “A mathematical theory of communication” étaient considérables. Il a beaucoup avancé son temps, il a proposé des solutions à de nombreux problèmes pratiques de l'avenir et tout d'une manière très élégante, avec des formules mathématiques et théorèmes et démontrant théorèmes.
...et plus encore

En plus de ces contributions majeures, Shannon a réalisé de nombreuses autres petites contributions. “Txiki”, pour ainsi dire, car ils sont petits par rapport à d'autres contributions, mais certains d'entre eux seraient suffisants pour toute autre renommée.
II. Pendant la guerre mondiale, avant d'écrire son article bien connu, Bell a travaillé en cryptographie dans les laboratoires et a fait quelques découvertes dans le domaine de la cryptographie. Cela lui a permis de rencontrer Alan Turing. Turing a parlé de l'idée de sa machine universelle, du concept d'ordinateurs actuels, qui, en définitive, se complétait parfaitement avec les idées de Shannon. À cette époque, Shannon a inventé des diagrammes de flux de signaux.
Shannon aimait les échecs et a également travaillé sur elle. En 1950, il a écrit un des premiers articles sur la problématique des programmes d'échecs informatiques, qui a lancé la région. Dans cet article, il a estimé que les combinaisons possibles du jeu d'échecs sont au moins 10 120, ce qui est maintenant connu comme le nombre de Shannon.
En 1950 il réalise la souris automatique Theseus, capable de trouver la sortie d'un labyrinthe et apprend le chemin pour après. Il s'agit du premier dispositif d'intelligence artificielle de ce type. Il aimait aussi les jongleries et dans les années 70 il a construit le premier robot jongleur. Il a également construit une machine qui a résolu le cube de Rubik.
Lors de ses voyages à Las Vegas avec certains de ses compagnons, il a gagné une fortune, car, en appliquant la théorie du jeu, ils ont compté des cartes et fabriqué un petit ordinateur caché (celui que certains considèrent comme le premier wearable) pour calculer les chances dans le jeu. Et avec des méthodes similaires, ils ont réussi à gagner encore plus en bourse.
Shannon est mort en 2001, après avoir subi la maladie d'Alzheimer au cours des dernières années. Lorsque vous avez perdu conscience de l'environnement, vos contributions ont déjà eu de nombreuses applications, mais n'a pas eu la chance de connaître les progrès et, surtout, la diffusion que vous avez eu ces dernières années sur Internet, les ordinateurs et autres appareils. Vous seriez sûrement surpris. Comme nous devrions nous étonner, parce que la personne qui a permis de réaliser cet énorme changement est presque inconnue.

Gai honi buruzko eduki gehiago
Elhuyarrek garatutako teknologia