Claude Shannon, father of the digital world
2016/09/01 Leturia Azkarate, Igor - Informatikaria eta ikertzailea Iturria: Elhuyar aldizkaria

Asked by the most important people in the world of Information and Communication Technologies, most people will probably not be able to give names beyond Bill Gates, Steve Jobs, etc. Those of us who know the world of computing better would surely say other names like Alan Turing or Tim Berners-Lee. Among us perhaps not so much would mention Claude Shannon. We don't know what the reason is, but Shannon doesn't have at all the fame that his immense contributions deserve; Shannon, for example, will be the most important name in the ICT world.
Claude Elwood was born on April 30, 1916 in a small town in the North American state of Michigan. From his childhood he taught in school the competence in science and mathematics, as well as the fondness for the invention and construction of mechanical and electrical devices. Thus, in 1932, at only 16 years old, he began his university studies at the University of Michigan, and in 1936 he completed his careers in mathematics and electrical engineering. Later, in 1936, he began to pursue a master's degree in electrical engineering at the prestigious Massachusetts Institute of Technology or MIT. And in 1940 he defended the doctoral thesis in mathematics at that same institution.
Fundamentals of Digital Electronics
However, the first of his two major contributions to science was made before the thesis, specifically in the master project, with only 21 years. According to several experts, it was the most important master's thesis in history.
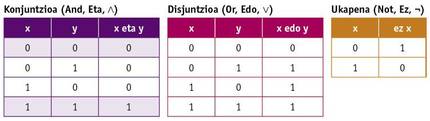
During the master's degree, Shannon was able to work with one of the most powerful computers of the time, Vannevar Bush's differential analyzer. Those computers at the time were analog, operated with pulleys, gears, etc. and occupied a large space. He also had the opportunity to know Boole algebra in his mathematics studies. In Boole algebra variables have no numerical value but Truth and Lie (or 0 and 1), and basic operations are not sum and multiplication, but conjunction, disjunction and negation (And, Or and Not). These operations are defined by the following tables of truth:
Shannon designed electrical circuit switches that implemented Boole algebra in the master project. In addition, he demonstrated that the combinations of these circuits allowed any mathematical or logical operation and designed some of them. This work laid the foundations for the design of digital circuits and from there came digital electronics. The computer and all other electronic and digital devices have come thanks to the vision he had in the project of his master.
Information theory, basis of information storage and digital communication
Although this contribution is truly impressive and surprising, it is considered its most important contribution. Shannon is mostly known for creating a field of knowledge of information theory and for its almost complete development, in 1948, when he worked in prestigious laboratories Bell, he wrote in his article “A mathematical theory of communication”.
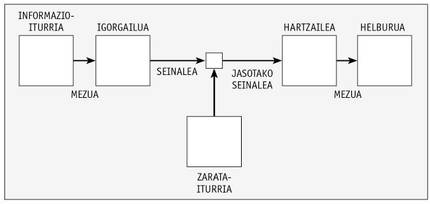
In this article, Shannon defined a communication system through the image below.
Thus, it analyzes and proposes ways to code the message in the most appropriate way. The image can be applied in the same way to a storage system in which an information is written in a medium in which the signal stored in it can suffer a degradation and must be the same as the written information when reading.
In the article, Shannon proposed converting information into a binary basis for storing and transporting information, that is, by numbers 0 and 1. These units of information were first indicated in that binary digit or bit article, although the name was J. W. It was the proposal of Tukey, Shannon's companion.
Turning information into digital was a breakthrough. In fact, the analog information used so far has more possible situations (actually infinite), and since the difference from one situation to another is small, any noise or small change in storage or transmission makes one signal become another and it is impossible to retrieve the original exact information. This caused major problems in the transmission of signals, for example, even by periodically raising the signal power with repeaters, as there was a degradation and loss of irreparable information. On the contrary, by moving the information to the binary base, there are only two possible situations, 0 and 1, and the difference between the two can be as large as desired in the physical signal (for example, 0 volts and 5 volts). Thus, although the signal is slightly degraded or modified, it is more difficult to convert 0 into 1 or vice versa. In this way, the information is stored more easily and reliably, and transmission can be carried out as far as desired by repeaters, without losing information.
This, for its part, was a breakthrough, but Shannon went further, defining virtually all mathematical techniques and formulas for current methods of compression and reliability in storage and communications.
For this he defined several concepts. One of them is the information that sends a message. In fact, Shannon said that not all messages give the same information: the more likely a message among all possible, the less information it gives. Also, among the symbols or characters of a message, a more frequent symbol provides less information. To measure the information of a symbol gave the formula I = –log2 p, where p is the probability or frequency of the symbol. This measurement of information also indicates the number of bits needed to transmit this symbol. Thus, we would need a bit to indicate each of the two results (leon or kastillo) that can be obtained when launching a coin, according to the formula. Or to represent each of the letters of a 27-letter alphabet, if everyone had the same probability, 4.76 bits would be needed.
He also defined the entropy of a message. The entropy of the message is the average information that contains a message, so it is defined as: H =|Pi log2 pi. Furthermore, since some of the symbols are more likely in some contexts than in others (in the case of letters, for example, it is common that after the q go the letter u, or after the consonants is more normal than a vowel than another consonant), Shannon also defined a conditioned entropy in which the previous sign is taken into account to calculate the probabilities. Well, this measure of entropy tells us to what extent a message can be compressed without losing information! In natural language messages, for example, taking into account the frequencies of the letters and the conditioned frequencies, entropy is less than one, so each letter can be encoded in signals of less than one bit. And how did Shannon. Lossless compression systems (ZIP, RAR or many others used in communications…) that are so much used today are based on Shannon formulas and methods.
Little with it, Shannon also theorized about lossy compression, and all the systems that use this type of compression (JPG, MP3, DivX…) have it basically.
And if that were not enough, he also wrote in that article about codes that detect and/or correct errors. To detect possible errors or correct errors in information received or read, redundant additional information is sent. Example of this are the control numbers in the account numbers or letters that have been added to the Spanish ID number. These are ultimately checksum or control sums. If we have failed in any number, the control sum will not match and we will know that there is an error in the number. To correct the error we will have to manually check since in these examples only the code is used to detect errors.
But there is a possibility to complete the original message even if there are errors in the received message. To do this, it is necessary to enter additional redundant information and, above all, that all possible words or numbers that can be sent in the code have a minimum distance from each other. So, suppose that the distance between all possible characters is three bits, if an error occurs in a bit we can know with enough certainty what character was wanted to send, if the probability of receiving two wrong bits of a signal is relatively small. This way, depending on the reliability of the channel, we will make a greater or lesser distance between the code signals (number of bits) and introduce more or less redundant information, but the receiver can also repair the wrong messages.
Error correcting codes were not invented by Shannon. His colleague Richard Hamming was the pioneer in it. But Shannon mathematically formalized error correction code theory and defined the maximum number of additional bits needed for different channel failure probabilities. And this formulation is the one that uses all the codes able today to correct the errors, with thousands of uses: in communications with spacecraft and others, in the storage of information in CDs and pen drives, etc.
As you can see, Shannon’s contributions in the article “A mathematical theory of communication” were enormous. He advanced his time a lot, proposed solutions to many practical problems of the future and everything in a very elegant way, with mathematical formulas and theorems and demonstrating theorems.
...and more

In addition to these main contributions, Shannon made many other small contributions. “Txiki”, so to speak, as they are small compared to other contributions, but some of them would be enough for any other fame.
II. During the World War, before writing his well-known article, Bell worked in cryptography in laboratories and made some discoveries in the field of cryptography. This allowed him to meet Alan Turing. Turing spoke of the idea of his universal machine, of the concept of today's computers, which ultimately complemented perfectly with Shannon's ideas. At that time, Shannon invented signal flow diagrams.
Shannon liked chess and also worked on it. In 1950 he wrote one of the first articles on the problem of computer chess programs, which launched the area. In this article he estimated that the possible combinations of the chess game are at least 10 120, which is now known as Shannon's number.
In 1950 he made the automatic mouse Theseus, able to find the exit of a labyrinth and learns the way for later. This is the first artificial intelligence device of this type. He also liked juggling and in the 1970s he built the first juggling robot. He also built a machine that solved Rubik's cube.
On his trips to Las Vegas with some of his companions he earned a fortune, since, applying the theory of the game, they counted cards and manufactured a small and hidden computer (which some consider the first wearable) to calculate odds in the game. And with similar methods they managed to win even more in stock.
Shannon died in 2001 after suffering from Alzheimer's in recent years. By the time he lost consciousness of the environment, his contributions already had numerous applications, but he did not have the opportunity to know the progress and, above all, the dissemination that have had in recent years Internet, computers and other devices. He would surely be surprised. As we should be surprised, because the person who allowed this enormous change to take place is almost unknown.

Gai honi buruzko eduki gehiago
Elhuyarrek garatutako teknologia