Claude Shannon, padre del mundo digital

Preguntados por las personas más importantes del mundo de las Tecnologías de la Información y la Comunicación, la mayoría de la gente probablemente no será capaz de dar nombres más allá de Bill Gates, Steve Jobs, etc. Los que conocemos mejor el mundo de la informática seguramente diríamos otros nombres como Alan Turing o Tim Berners-Lee. Entre nosotros quizás no tanto mencionarían a Claude Shannon. No sabemos cuál es la razón, pero Shannon no tiene en absoluto la fama que merecen sus inmensas aportaciones; Shannon, por ejemplo, será el nombre más importante del mundo de las TIC.
Claude Elwood nació el 30 de abril de 1916 en un pueblecito del estado norteamericano de Michigan. Desde su infancia enseñó en la escuela la competencia en ciencia y matemáticas, así como la afición por la invención y construcción de dispositivos mecánicos y eléctricos. Así, en 1932, con tan sólo 16 años, comienza sus estudios universitarios en la Universidad de Michigan, y en 1936 termina sus carreras de matemáticas e ingeniería eléctrica. Posteriormente, en 1936, comenzó a cursar un máster en ingeniería eléctrica en el prestigioso Massachusetts Institute of Technology o MIT. Y en 1940 defendió la tesis doctoral en matemáticas en esa misma institución.
Fundamentos de Electrónica Digital
Sin embargo, la primera de sus dos mayores aportaciones a la ciencia la realizó antes de la tesis, concretamente en el proyecto de máster, con tan sólo 21 años. Según varios expertos, fue la tesis de máster más importante de la historia.
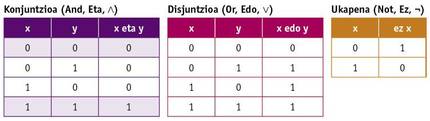
Durante la realización del máster, Shannon pudo trabajar con uno de los ordenadores más potentes de la época, el analizador diferencial de Vannevar Bush. Aquellos ordenadores de entonces eran analógicos, funcionaban con poleas, engranajes, etc. y ocupaban un gran espacio. También tuvo la oportunidad de conocer el álgebra de Boole en sus estudios de matemáticas. En el álgebra de Boole las variables no tienen valor numérico sino Verdad y Mentira (o 0 y 1), y las operaciones básicas no son suma y multiplicación, sino conjunción, disyunción y negación (And, Or y Not). Estas operaciones se definen mediante las siguientes tablas de la verdad:
Shannon diseñó en el proyecto del máster circuitos eléctricos de interruptores que implementaban el álgebra de Boole. Además, demostró que las combinaciones de estos circuitos permitían realizar cualquier operación matemática o lógica y diseñó algunos de ellos. Este trabajo sentó las bases para el diseño de circuitos digitales y de ahí surgió la electrónica digital. El ordenador y todos los demás dispositivos electrónicos y digitales han venido gracias a la visión que tuvo en el proyecto de su máster.
Teoría de la información, base del almacenamiento de información y comunicación digital
A pesar de que esta aportación es realmente impresionante y sorprendente, se considera su aportación más importante. Shannon es sobre todo conocido por la creación de un campo de conocimiento de la teoría de la información y por su desarrollo casi completo, en 1948, cuando trabajaba en prestigiosos laboratorios Bell, escribió en su artículo “A mathematical theory of communication”.
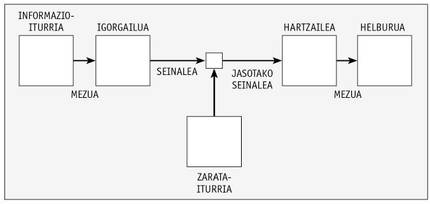
En este artículo, Shannon definió un sistema de comunicación a través de la imagen inferior.
Así, analiza y propone formas para codificar el mensaje de la manera más adecuada. La imagen se puede aplicar de la misma manera a un sistema de almacenamiento en el que se escribe una información en un medio en el que la señal almacenada en el mismo puede sufrir una degradación y debe ser la misma que la información escrita al leer.
En el artículo, Shannon propuso convertir la información en base binaria para el almacenamiento y transporte de la información, es decir, mediante los números 0 y 1. A estas unidades de información se les indicó por primera vez en dicho artículo binary digit o bit, aunque el nombre fuera J. W. Era la propuesta de Tukey, compañero de Shannon.
Convertir la información en digital era un gran avance. De hecho, la información analógica que se utilizaba hasta el momento tiene más situaciones posibles (infinitas en realidad), y dado que la diferencia de una situación a otra es pequeña, todo ruido o pequeño cambio en el almacenamiento o transmisión hace que una señal se convierta en otra y es imposible recuperar la información exacta original. Esto ocasionaba grandes problemas en la transmisión de las señales, por ejemplo, incluso levantando periódicamente la potencia de la señal con repetidores, ya que se producía una degradación y pérdida de información irreparable. Por el contrario, trasladando la información a la base binaria, sólo existen dos situaciones posibles, 0 y 1, y la diferencia entre ambas puede ser tan grande como se desee en la señal física (por ejemplo, 0 voltios y 5 voltios). Así, aunque la señal se degrade o modifica ligeramente, es más difícil convertir un 0 en un 1 o viceversa. De este modo, la información se almacena de forma más sencilla y fiable, y la transmisión se puede realizar tan lejos como se desee mediante repetidores, sin perder información.
Esto, por su parte, suponía un gran avance, pero Shannon fue más allá, definiendo prácticamente todas las técnicas y fórmulas matemáticas para los métodos actuales de compresión y fiabilidad en almacenamiento y comunicaciones.
Para ello definió varios conceptos. Una de ellas es la información que emite un mensaje. De hecho, Shannon dijo que no todos los mensajes dan la misma información: cuanto más probable es un mensaje entre todos los posibles, menos información da. Asimismo, entre los símbolos o caracteres de un mensaje, un símbolo más frecuente facilita menos información. Para medir la información de un símbolo dio la fórmula I = –log2 p, donde p es la probabilidad o frecuencia del símbolo. Esta medida de información, además, indica el número de bits necesarios para transmitir este símbolo. Así, necesitaríamos un bit para indicar cada uno de los dos resultados (leon o kastillo) que se pueden obtener al lanzar una moneda, según la fórmula. O para representar cada una de las letras de un alfabeto de 27 letras, si todos tuvieran la misma probabilidad, serían necesarios 4,76 bits.
También definió la entropía de un mensaje. La entropía del mensaje es la información media que contiene un mensaje, por lo que se define como: H =|Pi log2 pi. Además, dado que algunos de los símbolos son más probables en unos contextos que en otros (en el caso de las letras, por ejemplo, lo habitual es que después de la q vaya la letra u, o que después de las consonantes es más normal que una vocal que otra consonante), Shannon definió también una entropía condicionada en la que se tiene en cuenta el signo anterior para calcular las probabilidades. Pues bien, esta medida de la entropía nos dice hasta qué punto un mensaje se puede comprimir sin perder información! En los mensajes de lenguaje natural, por ejemplo, teniendo en cuenta las frecuencias de las letras y las frecuencias condicionadas, la entropía es menor que una, por lo que cada letra puede codificarse en señales de menos de un bit. Y cómo lo hizo Shannon. Los sistemas de compresión sin pérdidas (ZIP, RAR u otros muchos que se utilizan en las comunicaciones…) que tanto se utilizan en la actualidad están basados en fórmulas y métodos de Shannon.
Poco con ello, Shannon teorizó también sobre la compresión con pérdida, y todos los sistemas que utilizan este tipo de compresión (JPG, MP3, DivX…) lo tienen básicamente.
Y por si fuera poco, también escribió en ese artículo sobre códigos que detectan y/o subsanan errores. Para detectar posibles errores o subsanar errores en una información recibida o leída se envía fundamentalmente información adicional redundante. Ejemplo de ello son los números de control en los números de cuenta o letras que han añadido al número del DNI español. Estas son, en definitiva, las sumas de checksum o control. Si hemos fallado en algún número, la suma de control no coincidirá y sabremos que hay un error en el número. Para subsanar el error deberemos revisar manualmente ya que en estos ejemplos sólo se utiliza el código para detectar errores.
Pero existe la posibilidad de completar el mensaje original aunque haya errores en el mensaje recibido. Para ello es necesario introducir más información adicional redundante y, sobre todo, que todas las palabras o números posibles que se puedan enviar en el código tengan una distancia mínima entre sí. Así, supongamos que la distancia entre todos los caracteres posibles es de tres bits, si se produce un error en un bit podemos saber con suficiente certeza cuál era el carácter que se quería enviar, si la probabilidad de recibir dos bits erróneos de una señal es relativamente pequeña. De esta forma, dependiendo de la fiabilidad del canal, realizaremos una mayor o menor distancia entre las señales del código (número de bits) e introduciremos más o menos información redundante, pero el receptor podrá también reparar los mensajes erróneos.
Los códigos que corrigen errores no los inventó Shannon. Su compañero Richard Hamming era el pionero en ello. Pero Shannon formalizó matemáticamente la teoría de los códigos de corrección de errores y definió el número máximo de bits adicionales necesarios para diferentes probabilidades de fallo del canal. Y esta formulación es la que utilizan todos los códigos capaces hoy en día de subsanar los errores, con miles de usos: en las comunicaciones con naves espaciales y otras, en el almacenamiento de información en CDs y pendrives, etc.
Como veis, las aportaciones de Shannon en el artículo “A mathematical theory of communication” fueron ingentes. Se le adelantó mucho su tiempo, propuso soluciones a muchos problemas prácticos de futuro y todo de una manera muy elegante, con fórmulas y teoremas matemáticos y demostrando teoremas.
...y más aún

Además de estas aportaciones principales, Shannon realizó otras muchas pequeñas aportaciones. “Txiki”, por decirlo de alguna manera, ya que son pequeños en comparación con otras aportaciones, pero algunas de ellas serían suficientes para cualquier otra fama.
II. Durante la Guerra Mundial, antes de escribir su conocido artículo, Bell trabajó en criptografía en los laboratorios y realizó algunos descubrimientos en el campo de la criptografía. Esto le permitió conocer a Alan Turing. Turing habló de la idea de su máquina universal, del concepto de ordenadores actuales, que, en definitiva, se complementaba perfectamente con las ideas de Shannon. En aquella época, Shannon inventó diagramas de flujo de señales.
Shannon le gustaba el ajedrez y también trabajó en ello. En 1950 escribió uno de los primeros artículos sobre la problemática de los programas de ajedrez de los ordenadores, que puso en marcha el área. En este artículo estimó que las combinaciones posibles del juego de ajedrez son al menos 10 120, lo que hoy se conoce como número de Shannon.
En 1950 realiza el ratón automático Theseus, capaz de encontrar la salida de un laberinto y aprende el camino para después. Se trata del primer dispositivo de inteligencia artificial de este tipo. También le gustaban los malabarismos y en los años 70 construyó el primer robot malabarista. También construyó una máquina que resolvía el cubo de Rubik.
En sus viajes a Las Vegas junto a algunos de sus compañeros ganó una fortuna, ya que, aplicando la teoría del juego, contaban cartas y fabricaron un pequeño y escondible ordenador (el que algunos consideran el primer wearable) para calcular probabilidades en el juego. Y con métodos similares consiguieron ganar aún más en bolsa.
Shannon murió en 2001, después de haber sufrido el alzheimer en los últimos años. Para cuando perdió la conciencia del entorno, sus aportaciones ya tuvieron numerosas aplicaciones, pero no tuvo la oportunidad de conocer el progreso y, sobre todo, la difusión que han tenido en los últimos años Internet, los ordenadores y otros dispositivos. Seguramente se sorprendería. Como nosotros deberíamos sorprendernos, porque la persona que permitió llevar a cabo este enorme cambio es casi desconocida.
Buletina
Bidali zure helbide elektronikoa eta jaso asteroko buletina zure sarrera-ontzian