"Rompecabezas"

1989/01/01 Angulo, Patxi Iturria: Elhuyar aldizkaria

• Matematika

Desde los infantiles de 6, 8,… piezas hasta los de 3.000-5.000 piezas para personas tranquilas existe una gran variedad y en este tipo de cabezudos la dificultad aumenta con el número de piezas. Pero no son las que queremos traer aquí. Creemos que la dificultad no siempre está en los rompecabezas con muchas piezas. Las que aparecerán aquí, además de tener pocas piezas, las tendrás que hacer tú.

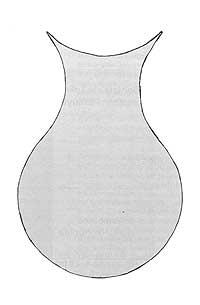
La primera es la maceta y cuadrada que tienes aquí. Te preguntarás si estas dos imágenes tienen algo que ver, siendo una redonda y otra cuadrada. Ahí está la clave, porque si se dividen bien las dos imágenes se puede convertir una en la otra. Si bien esta división se puede realizar de diversas formas, en este caso la dificultad no radica en la división multipieza, sino en la división mínima de piezas posible.

Queremos traer a este tipo de personas. Dos son el dodecágono y cuadrado y la estrella y cuadrada de seis vértices (Figuras 2 y 3). Aunque parezca mentira, es posible asociar imágenes de formas tan diferentes mediante una adecuada descomposición. Búscalo tú. Por supuesto, como en el caso anterior, la descomposición se debe intentar en el menor número posible de piezas. Para ello tenemos que decir que las medidas de las imágenes son precisas, es decir, si la estrella se divide, por ejemplo, el cuadrado que hay que conseguir es el de su lado. Es decir, son polígonos de la misma superficie.

Pero, ¿dónde está el origen de estos rompecabezas? Para responder a esta pregunta debemos ir a la historia.

a.C. En el siglo V, los matemáticos eran atraídos por cuestiones que hoy conocemos como “cuestiones clásicas de geometría”. Estas tres cuestiones eran la trisección del ángulo, la duplicación del cubo y la cuadratura del círculo. Esta última es la que nos interesa.

¿Por qué los matemáticos planteaban esta cuestión? Sin duda, la cuestión surgió cuando el radio o el diámetro obligaban a calcular la superficie del círculo, y desde este punto de partida se convirtió en cuestión geométricamente de equivalencia, dando el radio de un círculo para calcular la diferencia del cuadrado equivalente. Llegados a este punto, debemos decir que en aquella época no conocían el valor exacto del número de \{ (pi). Por lo tanto, la resolución de la cuestión no era tan sencilla como ahora.

Pero vamos a ver cómo lo consiguieron al cuadrado del círculo. Pitagórico VI. Ya en el siglo XX había resuelto el cuadratura de los polígonos (estos son nuestros responsables). Sin embargo, al pasar de los polígonos al círculo sus fórmulas y métodos eran inaplicables. Por lo tanto, los ensayos realizados sin medios especiales fracasaron.

En cambio, destacaron las sesiones de los sofistas Antifon y Brison. La primera, a partir de la emisión de un Polígono inscrito, se puede obtener otro de doble número de lados basado en la propiedad y a medida que el número de lados aumenta, el polígono se acerca al círculo, al ser todos los polígonos cuadrables se dedujo que el círculo también debería ser cuadrable. Una consecuencia falsa, como dijo Aristóteles: aunque el número de lados es muy elevado, el polígono nunca cumplirá el círculo. Brison, por su parte, añadió a lo dicho razonamientos análogos a los de los polígonos circunscritos, mostrando que las dos secuencias de polígonos abarcaban el círculo y que la superficie del círculo quedaba entre las superficies de dos polígonos, uno inscrito y otro circunscrito.

Este fue el camino que Arquímedes tomó para poner fin a esta cuestión. Sin embargo, para poder dar este último paso era necesario seguir dos más. El primero lo dio Hipias, la curva llamada cuadrador de Hipias. Lo definió en el siglo V. El segundo fue el matemático Dinostrato, que a través del cuadrador de Hipias podía corregirse la circunferencia. IV. Cuando lo demostró en el siglo XX. El último paso, como hemos dicho, lo dio Arkimedes. III. Cuando demostró que en el siglo XVIII se podía pasar de una circunferencia dirigida a un cuadro del círculo (mediante regla y compás). Los valores aproximados dados por Arquímedes para obtener esto para el número \{ (pi) eran 3 10/71 = 4’1408… y 3 1/7 = 3’1428…

Como hemos visto, las cuadraturas de los polígonos ayudaron a buscar la del círculo. Esto era precisamente lo que nosotros queríamos traer aquí. Y es que, como ya se ha mencionado anteriormente, con estas parejas de imágenes se pretende que tanto la maceta como la dodecágona o la estrella tengan la misma superficie que el cuadrado que tienen a su lado, es decir, manteniendo la superficie estas figuras deben convertirse en cuadrados.

Si te pedimos descomposición con las imágenes anteriores, esta vez nosotros te damos la descomposición de un cuadrado y tú tendrás que buscar el cuadrado (Figura 4). Este juego consta de sólo cinco piezas, pero su dificultad supera la de algunos puzzles de muchas piezas (medidas concretas).

También hay personas que se dedican a burlar, como lo que me ha dado un alumno de informática. Se llama pony de Loyd y se encuentra aquí (Figura 5). Se plantea:

“Con estas cinco piezas tienes que formar la imagen de un caballo, en la captura de la forma más aérea”.