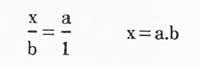"The Last Night"

1989/01/01 Angulo, Patxi Iturria: Elhuyar aldizkaria

• Matematika

From children of 6, 8,… pieces to those of 3,000-5,000 pieces for quiet people there is a great variety and in this type of heads the difficulty increases with the number of pieces. But they are not the ones we want to bring here. We believe that the difficulty is not always in puzzles with many pieces. Those that will appear here, besides having few pieces, you will have to do them.

The first is the pot and square that you have here. You will wonder if these two images have something to do, being a round and a square one. There is the key, because if you divide the two images well you can convert one to the other. Although this division can be performed in various ways, in this case the difficulty lies not in the multipart division, but in the minimum possible part division.

We want to bring this kind of people. Two are the dodecaine and square and the star and square of six vertices (Figures 2 and 3). Even if it seems to be a lie, it is possible to associate images in such different ways through proper decomposition. Look for it. Of course, as in the previous case, decomposition should be attempted in the least possible number of pieces. For this we have to say that the measurements of the images are accurate, that is, if the star is divided, for example, the square that must be achieved is the one on its side. That is, they are polygons of the same surface.

But where is the origin of these puzzles? To answer this question we must go to history.

BC. In the 5th century, mathematicians were attracted to issues we know today as “classical questions of geometry.” These three questions were the trisection of the angle, the doubling of the cube and the square of the circle. The latter is what interests us.

Why did mathematicians raise this question? Undoubtedly, the question arose when the radius or diameter forced to calculate the surface of the circle, and from this starting point became a geometrically equivalent question, giving the radius of a circle to calculate the difference of the equivalent square. At this point, we must say that at that time they did not know the exact value of the number of \{ (pi). Therefore, the resolution of the matter was not as simple as now.

But let's see how they got it to the circle square. Pythagorean VI. Already in the twentieth century had solved the square of the polygons (these are our responsible). However, when moving from polygons to circle their formulas and methods were inapplicable. Therefore, trials conducted without special means failed.

Instead, they highlighted the sessions of the sophists Antifon and Brison. The first, from the emission of an inscribed Polygon, can be obtained another of double number of sides based on the property and as the number of sides increases, the polygon approaches the circle, being all the square polygons it is deduced that the circle should also be quadrable. A false consequence, as Aristotle said: although the number of sides is very high, the polygon will never meet the circle. Brison, for his part, added to the said reasoning analogous to those of the circumscribed polygons, showing that the two sequences of polygons encompassed the circle and that the surface of the circle remained between the surfaces of two polygons, one inscribed and the other circumscribed.

This was the way Archimedes took to end this question. However, in order to take this last step it was necessary to follow two more. The first was given by Hipias, the curve called the Hipias quadrator. He defined it in the 5th century. The second was the mathematician Dinostrato, who could correct the circumference through the Hipias dial. IV. When he showed it in the twentieth century. The last step, as we have said, was taken by Arkimedes. III. When he showed that in the eighteenth century one could move from a circle directed to a circle (by ruler and compass). The approximate values given by Archimedes to obtain this for the number \{ (pi) were 3 10/71 = 4’1408… and 3 1/7 = 3’1428…

As we have seen, the squares of the polygons helped to find that of the circle. This was precisely what we wanted to bring here. As mentioned above, with these pairs of images, it is intended that both the pot and the dodecagone or the star have the same surface as the square next to them, that is, keeping the surface these figures must become square.

If we ask you to decompose with the images above, this time we give you the decomposition of a square and you will have to look for the square (Figure 4). This game consists of only five pieces, but its difficulty exceeds that of some puzzles of many pieces (concrete measures).

There are also people who are dedicated to mocking, like what a computer student has given me. It is called Loyd pony and is located here (Figure 5). It is proposed:

“With these five pieces you have to form the image of a horse, in capturing the most aerial form.”