Astronomia XVII. mendean

Giordano Bruno. Brunok Unibertsoaren mugak guztiz urruti zeudela eta gure Eguzki-sistema infinitu sistemaren artean beste bat baino ez dela esaten zuen. Esandako heresiengatik, Inkisizioak epaitu eta erre egin zuen.

Planeten higiduraren teoriak garapen izugarria izan du orain. 1600. urte inguruan gaude. Errenazimentua nahiz Erreforma pasatzen ari dira. Astronomiaren arloan bakar batzuek Koperniken sistemak eskaintzen zituen kalkulu-abantailak erabiltzen zituzten, baina bere ondorio fisiko nahiz filosofikoak onartu gabe. Ixilaldi honetan, zetorren gatazkaren adierazgarri ahots bakar bat entzu zen. Giordano Bruno-k (panteista antiortodoxo eta Europan zehar ibilitakoak) Unibertsoaren mugak guztiz urruti zeudela (hots, infinituan) eta gure Eguzki-sistema infinitu diren beste batzuen artean sistema bat baino ez dela esaten zuen. Esandako heresia guztiengatik, Inkisizioak epaitu ondoren 1600.ean erre egin zuen.

Hala eta guztiz ere, zientzia berri baten haziak tinko ari ziren ernetzen nonnahi. Ingalaterran Francis Bacon (1561-1626) eta William Gilbert (1540-1603); Italian Galileo Galilei (1564-1642); Kopenhage-n Tycho Brahe (1546-1601). Hau da grekoen garaiaz gero astronomi behaketetan hobekuntzak egin zituen lehen gizona. Ia bere bizi guztia, garai hartara arte ez bezalako zehaztasunez planeten higidurei behatzen iragan zuen. Bere datuak askotan Kopernikenak baino hogei aldiz zehatzagoak ziren eta guzti hori artean teleskopioa asmatu gabe zegoelarik.

Tycho Brahe hil ondoren, Johannes Kepler (1571-1630) alemanak eman zion segida, alde batetik beste behaketa batzuk eginez eta bestetik hartutako datu guztien ikerketa sakona eginez. Tychok bere garaian planeta-sistema berezia garatu zuen bitartean, Kepler Koperniken alde zegoen. Bere lanen helburua honakoa zen: aldi hartan zeuden planeten higiduren astronomi taulak baino zehatzagoak egitea. Baina, oinarrian teoria heliozentrikoa egokitzea baino ez zuen nahi, zeren bere harmonia eta erraztasuna zirela eta, berak liluratuta eta oso gustora ikusten bait zuen teoria hura. Bere lanen hasiera-hasieratik metafisika pitagorikoak eta neoplatonikoak izugarrizko eragina izan zuten. Joera honek Errenazimentuan zehar segitu zuen, Aristotelesen nagusitasunari desafio eginez.

Keplerren eritziz Jainkoaren adimenaren joera nolabait geometrikoa zen eta ordenu horren ezaugarriak sistema heliozentrikoa gidatzen zuten erlazio matematikoetan aurki zitezkeen. Horregatik, bere aurrenetako lan batean ezagutzen ziren sei planetak eta beren Eguzkiarekiko distantziak geometriako bost solido erregularrekin erlazionatu nahi zituen.

Martitzen orbitaz lortutako datu berriak Koperniken sisteman egokitu nahi zituenean eta lau urtez gogor lan egin ondoren, oso garrantzi handiko ondorio batera iritsi zen, hots, ezinezkoa zela! Datu berriek orbita Koperniken eskemakotik zortzi minutura kokatzen zuten. Kopernikek bere garaian, erabilitako datuak zehatzak ez zirela jakinda, ez zion diferentzia horri garrantzirik eman, baina Keplerrek bazekien Tychoren datuak esandako diferentzia baino askoz zehatzagoak zirela eta, beraz, lortutakoa onartezina zela. Horregatik, eta zientzilariei dagokien zintzotasunaz, ez zen saiatu behaketak ukatzen eta bereak aldez aurretik onartutako teoria salbatzeko beste hipotesi berri batzuk asmatzen. Aldiz, berarentzat zortzi minutu horiek honakoa adierazten zuten: Koperniken sistema ez zela Martitzen higidura erreala adierazteko gai. Beraz, Koperniken sistema, bere esfera zentrukideekin eta epizikloekin, bazter batera utzi zuen.

Keplerrentzat hori oso gogorra izango zen; bera zinez Koperniken sistemaren aldekoa bait zen. Hala ere aurrera segitu zuen eta horretarako Koperniken sistema antzinako Greziarekin lotzen zuen uztarria apurtu egin behar izan zuen. Teoria heliozentrikoaren arabera planeten ibilbideak estudiatzen zituenean hauxe bururatu zitzaion: behar bada ibilbideen irudia elipsearena izan zitekeela (elipsearen ezaugarriak K.a. II. mendeaz gero ezagunak ziren). Hori onartuz gero, hau da, planeta baten berezko ibilbidea elipsea dela, erraztasun handiko eskema geometrikoa eraikitzen zen munduarentzat. Eskema horretan, planeta guztiak orbita eliptikotan mugitzen dira, Eguzkia foku batean egonik. Lege hau Keplerren hiru lege nagusietako bat da eta gehienetan l ehenengo legea dela esaten da.

Eguzki-sistemaren lerro eskematikoak, orbiten tamaina erlatiboak erakutsiz. Planeten tamaina erlatiboak eskala desberdinetan daude. Koadroan Plutonen orbita osoa ikus daiteke.

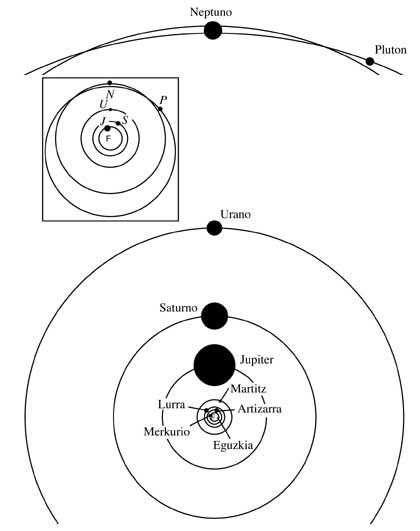
Keplerren lehenengo lege honek, Koperniken teoria heliozentrikoa zuzentzean, eguzki-sistemaren oso irudi erraza ematen digu. Koperniken epiziklo nahiz eszentriko guztiak baztertu egiten dira: orbitak elipseak baino ez dira. Irudian eguzki-sistemaren oraingo eskema sinplea dugu

Elipse hauek ia zirkuluak dira eta orbita guztiak ia plano berean daude, Plutonena izan ezik. Honek inklinazio gogorra dauka eta irudian nahiz bestela Neptunoren eta Plutonen orbitak espazioko inongo puntutan ez dira guruztatzen.

Seguru asko Kepler zoriontsu izan zen honelako ondorio errazera iritsita eta (oso konplikatuak ziren epiziklo eta eszentrikoak alde batera utzi ondoren) elipseen bitartez dena ondo betetzen zela ikusita. Baina hala ere, bere buruan kezka bat zuen: guk Platonek higidura zirkular eta uniformeak naturalak zirela onartzeko zeukan joera uler dezakegu, baina Naturak zergatik aukeratzen du elipsea? Galdera horri behar bezala erantzuteko Newton etorri arte itxaron behar da; Newtonek elipsearen legea askoz zabalagoa den Naturaren beste lege baten ondorio bat baino ez dela adierazi bait zigun. Beraz, oraingoz utz dezagun gaia horrenbestez.

Horregatik, Keplerren lehen legea egindako behaketen laburpena dela pentsatu behar dugu, hots, lege enpirikoa dela. Baina, lege honek planeta baten kokaleku guztien berri ematen badigu ere, ez digu planeta hori toki batean edo bestean noiz izango denari buruz ezer esaten, hau da, orbitaren irudia adierazten digu, baina bere abiadura ez. Beraz, lege hau oso motz gelditzen da astronomoek (eta Keplerrek ere bai) planeta bat puntu batean noiz izango den aldez aurretik jakin nahi dutelako. Horregatik, bere lehen legea plazaratu aurretik Keplerrek bigarren legea ezarrita zeukan; planeta baten abiaduraren aldaketak adierazten dizkiguna, hain zuzen.

Johannes Keplerren langelako alderdi bat.

Keplerrek honako hau zekien: planeta baten orbitaren posizio bateko eta besteko abiaduraren artean erlazio matematikoa egongo balitz, sistema askoz errazagoa izango litzatekeela. Erlazio hori aurkituko balitz, planeta baten higidura oso datu gutxiren bidez adieraz zitekeen. Bi datu behar ziren elipse bera emateko, hirugarrena ibilbidearen puntu zehatz bateko abiadura izateko (perihelioan, adibidez, hau da, planeta Eguzkitik hurbilena dagoen puntuan) eta beste bat orbita-planoaren beste planetekiko inklinazioa ezagutzeko. Baina, erlazio haren berri inork ez zuen. Horregatik, lege hau bururatu zitzaionean estasian zegoela esan ohi da, baina dakiguna beste hau da: lege hori aurkitzeko izugarrizko datu-piloa aztertu behar izan zuela eta etengabeko lan gogor eta sendoa burutu zuela.

Dena dela, bigarren lege hau lortzeko ibili zuen bidea harrigarria da, zeren hiru hipotesi okerretan oinarrituta ondorio zuzenera iritsi bait zen. Keplerren eritziz, planetek deskribatzen duten orbita Eguzkiak eragiten dien indarrari zor zaie eta indar horren balioa Eguzkiaren eta planetaren arteko distantziarekiko alderantziz proportzionala zen. Planetaren abiadura eta bultzada eragiten dion indarra elkarrekiko zuzenki proportzionalak ziren eta, beraz, distantziarekiko alderantziz proportzionalak. Hipotesi hau (hots, abiadura indarrarekiko proportzionala izatea) gaur egun onartezina da, baina Aristotelesen ideia bezala ikus daiteke edo bestela garai hartan sen onak ematen zuen zerbait bezala.

Hipotesi honen arabera, ibilbidean planeta batek distantzia txiki bat ibiltzeko behar duen denbora Eguzkirainoko distantziarekiko proportzionala izango litzateke. Hau ia erabat zuzena da eta orbitaren zenbait puntutan hala da. Beraz, Keplerrek ibilbidearen tarte handi bat (eta beraz Eguzkirainoko distantzia aldakorra denean) osatzeko behar den denbora kalkulatu nahi zuen. Horretarako, tarte handi hori osatzen duten arku txiki guztien distantziak hartu zituen kontutan eta denbora hori Eguzkitik planetaraino doan lerroak estaltzen duen azalerarekiko zuzenki proportzionala dela ondorioztatu zuen. Bigarren lege honen arabera, Lurra (edo nahi bada Eguzkia izarren hondoan) neguan udan baino azkarrago higitzen dela ulertzen da eta hori bai Keplerrek eta bai bere aurrekoek ongi ezagutzen zuten.

Bi lege hauek 1609an plazaratu ziren Astronomia Nova izeneko liburuan. Baina Kepler ez zegoen gustora eta kezka bat zeukan: planeta desberdinen higiduren arteko inongo erlaziorik ez zen ezagutzen. Planeta bakoitza bere elipsean eta bere abiaduraz higitzen zen, baina zirudienez, ez zegoen eredu orokor bat denentzat. Keplerrek eredu orokor horrek egon behar zuela pentsatzen zuen eta, beraz, eguzki-sisteman dauden higidura guztiak lotzen dituen erlazio batek egon behar zuen. Erlazio horren atzetik abiatu zen Kepler eta horretarako musika-teoria erabili ere egin zuen, Pitagorasen jarraitzaileen arabera, planeten orbiten eta musikako noten artean lotura baten bila. Bere lan oparoari Munduaren harmoniak izena eman bazion, zer edo zer adierazi nahi zuen.

Erlazio horretan sinesteak (edo hobeto esan, zeukan obsesioak), alde batetik Keplerrek zeukan zenbakiekiko hasierako fede magikoa edo adieraz dezake, baina baita zientziaren alorreko jenio guztiek izan duten joera ere. Hauen eritziz Natura uniformea eta erraza da. Sinesmen horrek izugarrizko laguntza eman die zientzilariei eta oztopoak gainditzeko indarra ere bai. Hauetakoa dugu Kepler, zeren mila zorigaitz pertsonal jasan behar izanagatik bere hirugarren legea aurkitu ondoren hau idazteko gai izan bait zen:

Keplerren tauletako frontisa.

... denbora luzez etengabeko lanez Braheren datuak erabiliz orbiten benetako distantzia aurkitu ondoren, azkenean egiazko erlazioa... gaur egun aurkezten dudan lanaren eta Braheren behaketez hamazazpi urtetan zehar nik egindako lanaren artean hain adostasun handia egoteak nire adimenetik itzalak garbitu egin zituen eta hasieran ametsetan nengoela usten nuen...

Lege honek gaurko hizkeraren arabera honela dio: planeta baten periodoa T bada (hau da, Eguzkiaren inguruan bira oso bat emateko denbora alegia) eta R bere batezbesteko erradioa, T ² = K . R ³ da, K hori planeta guztientzat balio bera duen konstantea izanik. Lurraren kasuan T = 1 urte eta R = 15 x 10 ⁷ km eta beraz, beste edozein planetarentzat bere R erradioa ezagutuz gero periodoa aurki dezakegu.

Hirugarren lege honi lege harmonikoa esaten zaio, planeten arteko erlazio harmoniko polita adierazten duelako.

Guzti honen bitartez, gure eguzki-sistema logikoki erlazionatuta osotasun sinple bat bezala ikusten dugu: gure adimenak Keplerren unibertsoa begirada batez bereganatzen du eta unibertsoa gidatzen duten legeak matematikaren bidez adierazteko gai dira.

Kepler, Braheren datuetan oinarrituta planeten higiduren taula zehatzak eraikitzen saiatu zen. Lan hura egiteko garai hartan onartuta zeuden eritzi batzuk alboratu egin behar izan zituen. Jarrera hura guztiz berria zen, hau da, behaketei lehentasuna ematearena, baldin eta behaketa horiek zehatz eta kuantitatiboki egiten baziren. Beste alderdi bat ere azpimarratu behar dugu: lege fisikoak adierazteko hizkuntza matematikoa erabiltzearen igarpena. Harez gero ekuazioak lege fisikoen adierazpen naturalak izango ziren.

Bestalde, Keplerren sisteman planetak beren orbitan higitzea ez zen inolako jainkoren eraginez gertatzen zela kontsideratzen (eskolastikoek erakusten zuten bezala) eta ezta beren itxura esferikoek higidura zirkularrak adierazten zituztela ere. Bere azken aldiko liburu batean ( Mysterium Cosmographicum ) izenekoan, 1596ean bere eritziak nola aldatu zituen esaten digu:

Johannes Kepler. Aldi hartan planeten higidurei buruz zeuden astronomi taulak baino taula zehatzagoak egitea zen bere lanen helburua.

Garai batean planeta baten higiduraren indarra arima batean zegoela sendo sinesten nuen... Hala ere, higiduraren kausa hori distantziarekin batera txikiagotu egiten zela hausnartu nuenean (hau da, Eguzkiaren argia astro horrekiko distantziarekin batera txikiagotu egiten den bezala), indar horrek substantziala izan behar zuenaren ondoriora iritsi nintzen; ez hitzez hitz hartuta, baizik... argia zerbait substantziala dela esaten dugunean bezala, hau da, zerbait ez-espirituala eta gorputz substantzial batetik irteten dena.

1605ean lagun bati honakoa idatzi zion:

Kausa fisikoen ikerketaz asko arduratu naiz. Nire saiakuntza hau frogatzea izan da: zeru-makina jainkozko organismo batekin ez eta erlojeri lan batekin konparatu behar dela (eta erloju batek arima baduela sinesten duenak, ohorea erlojugileari egozten dio), eta erloju hartan higidura desberdin guztiak indar magnetiko sinple baten emaitzak dira, hala nola erloju baten makinaren higidura guztiak pisu bakar baten ondorio diren bezala. Gainera, kontzeptzio fisiko hau kalkulu eta geometriaren bitartez adierazi behar dela frogatzen dut.

Keplerrengan bi mende lehenago Europan hasitako aldaketa ikus dezakegu argi. Egunetik egunera behaketak, emaitzak, hitz batez, errealitateak espekulazio hutsei lekua kentzen diete eta teoriek errealitate horretan oinarritu beharko dute. Horregatik, Keplerrek zientziaren jarrera modernorako lehen aldarrikapena egin zuela esan dezakegu.