Rincón del lector. Abril

1989/04/01 Arregi Bengoa, Jesus Iturria: Elhuyar aldizkaria

• Astronomia

PREGUNTA

¿Un universo finito o infinito?

ELHUYAR. En el número 19 de la revista ZIENTZIA ETA TEKNIKA, en la sección "El Rincón del Lector", de Jesús Arregi, creo que una idea está equivocada.

En el citado artículo se afirma que: Si la fuerza de gravedad de la materia en el universo es suficiente para frenar la velocidad de alejamiento y producir contracción, el universo es finito. Sino infinito.

Creo que si la fuerza de gravedad de la materia es suficiente para frenar la velocidad de alejamiento y producir contracción, la expansión será cada vez más lenta, convirtiéndose en contracción, lo que hace que el universo sea pulsable. Si no, aunque siempre haya sido finito, sus medidas serán cada vez mayores.

Siendo la velocidad de la luz la mayor del universo y aceptándose la existencia de la constante de Hubble (expansión y base de la teoría del “Big Bang”), la mayor distancia entre dos puntos del universo puede alcanzar los 12.500 millones de años luz. Véase el tomo 11 Elhuyar, número 1. 1985 Pasado y futuro del Universo. Sección 3ª.

Si la masa del universo no fuera suficiente para producir contracción, la finitud del amasado (sus medidas geométricas) sería cada vez mayor, pero finita aun así, aunque esa finitud no tuviera límites.

Ponemos un ejemplo sencillo: el conjunto de los números naturales es infinito, pero todos los números naturales son finitos.

Por lo tanto, para terminar, no hay que confundir los dos conceptos: los márgenes del universo o los límites geométricos (que no existen), con los límites o límites matemáticos de las medidas del universo. La posible existencia de esta última radica en la cantidad de masa invisible.

Antón del Campo

RESPUESTA

Para comprender los resultados que se obtienen al aplicar la Teoría de la Relatividad General a la totalidad del universo, es necesario recurrir a situaciones de mecánica clásica. Por ello, muchas veces estas analogías se extraen de sus medidas y se crean errores porque las diferencias no se subrayan. Eso es lo que a menudo ocurre en la analogía entre la evolución de la expansión del universo y el problema de la velocidad que un cuerpo necesita para escapar de la gravedad de otro.

Pensemos, para explicar el segundo caso, que queremos lanzar un lanzador para salir de la Tierra. A la hora de realizar la prueba se nos presentan tres opciones en función de la velocidad que damos al lanzador. En la primera, cuando la velocidad del lanzador es menor que la necesaria para superar la atracción (que llamamos velocidad de escape), el objetivo no se consigue y el tema de escape cae hacia la atracción. En los otros dos, cuando la velocidad del lanzador es igual a la velocidad de escape o la primera es mayor, se alcanza el objetivo, teniendo como único separador la diferencia de velocidades relativas entre los cuerpos al final del proceso.

La paridad entre estas conclusiones y las que se derivan del análisis cosmológico de la expansión del universo no es total, y creo que de esa equiparación equivocada has deducido lo que me propones en tu escrito.

Dentro de la Mecánica Clásica es posible que suceda lo que planteas, es decir, que el lanzador sea un universo finito que se expanda para siempre con mayor energía que el correspondiente a la velocidad de escape. (En definitiva, debemos considerar que el universo está formado únicamente por la Tierra y los lanzadores. El “Big Bang” sería el encendido de los motores del último). Esta composición, sin embargo, no es justa, dentro de la Cosmología relativista. Según la Relatividad General, el efecto de la gravedad es consecuencia de las deformaciones o curvaturas que produce la materia en el espacio/tiempo tetradimensional.

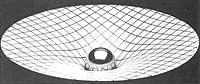
Por tanto, la división de la materia que juega contra la expansión del universo limita su forma y dimensiones. Si la influencia de la gravedad es en concreto suficiente para frenar la expansión y producir contracción, la curvatura es positiva y los tres componentes espaciales del espacio/tiempo tetradimensional se agacharan alrededor de sí mismos hasta que se cierra como la superficie de una esfera bidimensional. En este caso el universo es finito, por supuesto; de lo contrario, el cierre de los geodésicos sería imposible. En cuanto a la cuarta dimensión, es decir, el tiempo, y a nosotros, podemos decir que tiene un principio con el "Big Bang" y se termina cuando el universo vuelve a la singularidad por contracción.

Por lo tanto, la finitud es la peculiaridad del espacio y del tiempo y no puede ocurrir que el tiempo de una situación en el espacio finito sea infinito o viceversa. Si la influencia de la gravedad no es suficiente para producir contracción, la extensión se mantendrá siempre. La curvatura espacio/tiempo en este caso es cero o negativo y en cualquier caso las dimensiones espaciales no se cierran. Por lo tanto, son infinitos. El tiempo también es así, porque aunque empieza con el "Big Bang" no tiene fin. A estos universos les llamamos “abiertos”.

Como hemos dicho, sólo hay dos opciones:

• Si la influencia de la gravedad es mayor que el límite de contracción, el universo es finito (también en el tiempo) y cerrado.
• Si la influencia de la gravedad es más débil que la frontera, el universo es infinito y abierto.

Tal y como destacábamos arriba, las particularidades que se mencionan en cada una de las dos opciones están íntimamente relacionadas y son inseparables. Por el contrario, la situación que usted propone requiere que las dimensiones espaciales sean finitas y temporales infinitas (un universo finito que se expande constantemente), y dentro de la Relatividad General no hay lugar para esta opción: si el espacio es finito también el tiempo, si el tiempo es infinito también el espacio.

Por todo ello, considero que la afirmación que cita es correcta.

Estoy de acuerdo con el cálculo correspondiente a la distancia máxima entre dos puntos del universo, pero hay que tener en cuenta que ese cálculo corresponde al universo observable y es útil tanto si éste es finito como infinito.

Tienes razón subrayando la diferencia entre límites geométricos o márgenes y límites de medidas. La diferencia es evidente y por eso no es necesario mencionar a los primeros para hablar por segunda vez, como he tratado esta vez. En la respuesta anterior mencioné las dos para subrayar las diferencias entre ambas y quizás no conseguí el objetivo.

Jesús Arregi.