A fable of numerical methods: .. and to eat, high-frequency waves
2012/04/01 Alberdi Celaya, Elisabete - Matematikan lizentziatua eta doktoregaia Iturria: Elhuyar aldizkaria
Numerical methods
Differential equations were of great importance. There they were when we had to study a new business opportunity in any company, even when, applying some interest rates, we wanted to know the amount of money that would have existed in the banks after a few years, or among the engineers of a construction company, when they were studying the vibrations that could withstand the new bridge that was being built in the neighboring village, or in a chemistry laboratory when the temperature dispersion of a surface was to be calculated... All of them led various companies and research centers to identify and define the need for a new job, corresponding to the numerical method. His work was to solve analytically, that is, to release differential equations that could not be resolved or that did not interest to solve exactly. For this, with the necessary operations, they obtained an approximation to the result of the differential equation.
When a numerical method had to be hired somewhere like this, an ad was put in the press, just like any other job. And so did the staff officer who was conducting the interview at the time: "An important company in the Bilbao environment dedicated to building construction needs a numerical method. It must be able to release differential equations in low orders and little influenced by disturbances or problems arising from the medium. Experience in solving vibration-related problems will be assessed. Taste for high-frequency waves is critical. It offers a good salary and the possibility to use the gym of the company."
The curricula of candidates received for the position were analyzed. The numerical method took into account intellectual and psychological capabilities. Among intellectuals, the precision with which the method could solve the differential equation was taken into account. "I have been designed and programmed to solve problems precisely in different orders," said one that for the approximate result sought the company could solve the differential equations with the desired precision (large or small). Others only worked in first or second order, that is, in low orders and therefore with little precision. When the project in the company's hands needed more precision, those who released under low orders were not hired. This did not mean that there were no companies for hiring workers who worked for these orders, which in others could have been hired, of course.
Regarding psychological capabilities, the contracting company wanted to know the stability field of the numerical method. This determined the response of the method to errors or disturbances that occurred when the equations were released. The method also reflected his ability to familiarize himself with the peculiarities of the differential equation --self-values -. The fact that the method had a wide stability field indicated that it had the capacity to act in the face of various problems. A smaller stability area, however, could demonstrate that in the face of certain disturbances the method would not yield satisfactory results. In these cases, disturbances in problems resolved outside the stability zone increased and the calculated result could become less good or bad.
How much do you charge? "For computational cost". What was able to work on high orders and avoid disturbances was costly. Thus, the work of several mathematicians focused on the design of these methods.
Spectral radio
However, there was some feature that was more hidden by the numerical method. One of the hidden features was the so-called algorithmic cushioning. This showed the behavior of the method with high frequency waves.
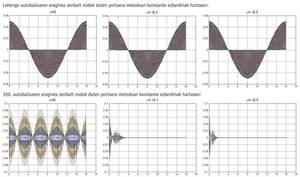
There were numerical methods of high and stable order but they did not have good behavior with high frequency waves. This meant that when we were releasing differential equations in which high frequencies appeared there were methods that tended to abuse high frequencies. In the waveform differential equations, if theoretically the wave was vibrating in a time interval, the approximate result of these numerical methods was losing, among other things, its amplitude, being able to even completely disappear the wave. On the contrary, there were methods that did not even look at high-frequency waves, that is, they did not eat them. But sometimes that wasn't good either.
When we are releasing a differential equation in an approximate way, it is customary to divide the field in which we must calculate the solution into elements, that is, to disagree the problem. The ends of each element are called nodes. Once the field is divided into elements, the numerical method is applied to the problem. This problem will have some self-values, some smaller and others larger. Small self-values provide low frequency waves and high frequency large waves. And all the self-values of the problem influence the result. What happens is that the big autobalies are often a consequence of the discretization, so they do not bring anything or nothing good in the final result. Therefore, when we are releasing a differential equation by numerical methods, in addition to an order and stability, we are interested in applying a method that partly consumes those high-frequency waves that may be a consequence of discretization. That is, the key to the problem is that the numerical method we will apply is able to moderate the consumption of high-frequency waves.
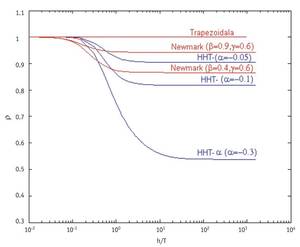
Each method has associated an amplification factor. The largest module of this amplification factor is called spectral radius. The value of this spectral radius depends, moreover, on the size and period of the step we are going to take in the method with which we will release the differential equation. The spectral radius corresponding to the cases in which when dividing the size of the step by the period is obtained a low value, shows the behavior of the numerical method with the low-frequency waves. On the contrary, the spectral radio corresponding to the cases in which a large number is obtained by dividing the size of the passage by the period, will tell us how the numerical method will behave with high-frequency waves. If as the step size increases by dividing the period, the spectral radius value decreases, this means that the method will tend to dampen the high-frequency waves.
The methods of the Newmark family obtained by giving values to two parameters (<,{) are of order 2 for{ = 1/2 and have quite good stability characteristics. When in the Newmark method we take the values < = 1/4,{ = 1/2, we get the so-called trapezoidal method, of order 2 and with a high stability zone. In addition, the value of the spectral radius is always the unit. This means that it will keep the waves high and low frequency without slowing down anything. This is good in part, as with the passage of time the wave will remain complete, but on the other hand it is not so good, since the damping of high frequency waves derived from discretization can come well.
The hht-<unk> method is built based on the Newmark method and is obtained by assigning values to three parameters (<unk>, <,{). And when we choose e [-1/3, 0],{ = 1 - 2 to /2 and < = (1 - 2 to ) 2 /4, the hht-<unk> method is of order 2, has good stability characteristics and also manages to dampen the high frequency. This is good because the method will reduce the effect of high frequencies derived from discretization. When in the hht-<unk> method we choose <unk> = 0 we get the Newmark family. And taking <unk> = 0 in the expressions of{ y < mentioned, you get the trapezoidal method of the Newmark family.
The key: adapt to each method the work that can do well
As in other jobs, the key was the adequacy of the work that would best perform to each numerical method. The staff manager had a question: one of the requirements they put in the announcement was that the numerical method they were going to hire was the taste for high-frequency waves, but to what extent did you like it?
The staff officer addressed the method he had just interviewed as follows: "I have to do a small test to secure your order and stability zone and calculate your spectral radius."
Once the test was carried out and once the results of these characteristics were obtained by the personnel responsible, the method was corrected as follows: "I see that you have the capacity to act on low orders. You have a very good stability zone, almost nothing stimulates you. Also, as far as spectral radio is concerned, I observe that it only affects to some extent the high-frequency waves, not too much, not too much. It is suitable for the problems we have to release. Welcome to our experienced construction company."
Thus, the important Bilbao company dedicated to building contracted the hht-alpha method.
BIBLIOGRAPHY
Gai honi buruzko eduki gehiago
Elhuyarrek garatutako teknologia
