Poliminos (II)

1990/02/01 Angulo, Patxi Iturria: Elhuyar aldizkaria

• Matematika

No número anterior falamos dos poliminos. Da palabra “domino” sacamos as palabras trimino, tetramino, pentamino, hexamino e, en xeral, polimino. Nela obtiñamos os xogos de polimino identificando dous mino, talles como trimino>tres mino, tetramino -catro mino, pentamino -cinco mino e hexamino -seis minos. En todos eles aceptamos a equivalencia mino?

Neste número ampliaremos o concepto de “mino” e, ademais do cadro, darémoslle significados de triángulo equilátero e hexágono. A razón é que o único polígono regular que pode formar o plano sexa o do tres mencionados, o cadrado, o triángulo equilátero e o hexágono.

Comezando cos triángulos equiláteros e seguindo o mesmo desenvolvemento, formaremos xogos triangulares de dominios, triminos, tetraminos, pentaminos e hexaminos. Todas as pezas destes xogos son:

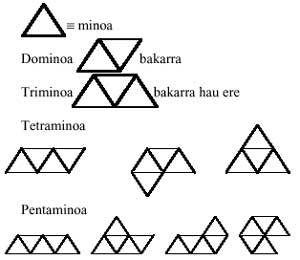
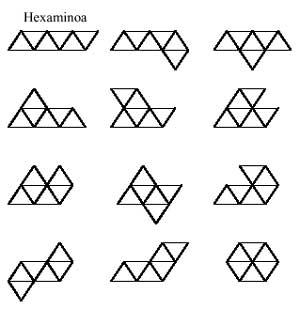
Vénnos á cabeza una pregunta: pódense formar pentaminos con medos e triminos? E despois outra: e pódense formar hexaminos con dous triminos?. E outro: pódense formar hexaminos con dominos e tetraminos?. A resposta á primeira é afirmativa. Pero o dos demais non. Cales son os examinos que non poden formar dous triminos? e os que non poden formarse mediante a unión de dominios e tetraminos?

Os tetraminos ofrécennos outra alternativa, é dicir, pódese dicir que os tetraminos son desenvolvementos lisos do tetraedro?. Ou devandito doutro xeito, pódese completar o tetraedro con tetraminos?

A continuación preséntanse tres imaxes que poden estar formadas por pentaminos triangulares:

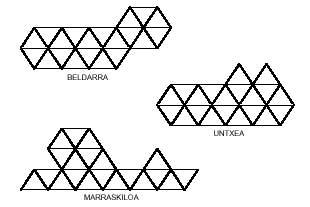
A resposta é para que tentes completar doce hexaminos.

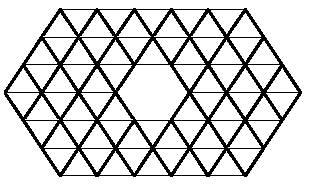
Deixamos os polímeros triangulares con este último.

Antes de seguir adiante, por suposto, a forma máis sinxela de responder as preguntas aquí expostas é a través da elaboración de poliminos, que che recomendamos.

Pasemos agora aos polímeros hexagonales.

Os polímeros hexagonales, como non podía ser doutra maneira, componse de hexágonos, que é o que imos facer agora, tomando como mínimo o hexágono:

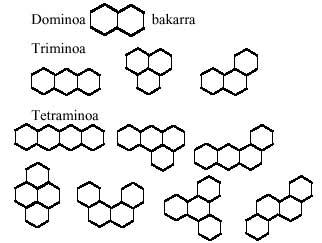
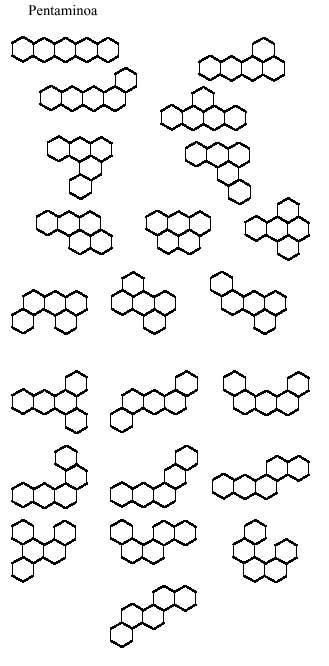
Os hexagonales non se traen xa que hai 82 hexaminos diferentes. A verdade é que o número de pentaminos (22) queda bastante grande paira xogar con eles. Con todo, máis adiante propómosche algunhas imaxes.

Paira completar con tetraminos hexagonales propómosche as seguintes imaxes (ver imaxe adxunta), pero una das oito non se pode completar.

Tes que buscalo ti. En todos eles serán necesarios sete tetraminos.

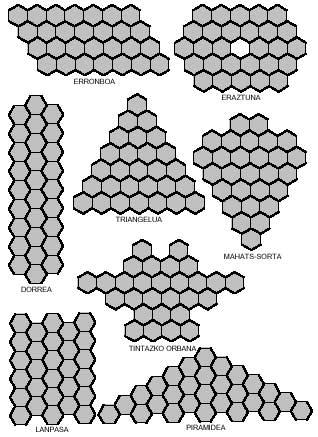
Tamén se poden obter imaxes curiosas con pentaminos hexagonales como os da seguinte figura. Catro delas, como se ve, pódense dividir en dous partes, e en ambas, no rombo e no corredor, colocando as dúas partes doutra maneira, pódense conseguir rombos e lanpas máis longos.

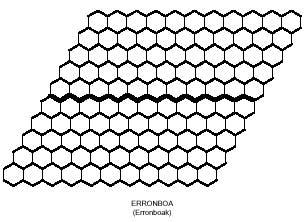
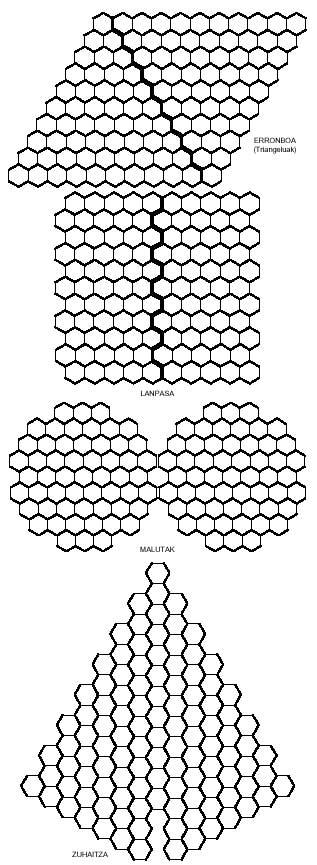
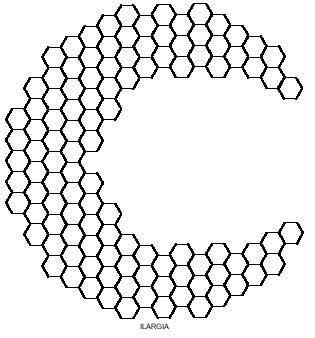
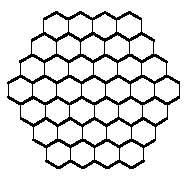
Do mesmo xeito que tratabamos de formar rectángulos con polímeros cadrados, cos polímeros hexagonales poderiamos tentar construír hexágonos. Os hexágonos formados por hexágonos necesitan 1, 7, 19, 37, 61, 91, 127,… hexágonos. Estas cantidades non son alcanzadas polos triminos (9), nin polos tetraminos (28) nin polos pentaminos (110). Pero se vos decatades, a unión de trimino e tetramino permite formar un hexágono de 37 hexágonos. Pero realmente pódese completar devandito hexágono con tres triminos e sete tetraminos? Aí tes outra pregunta para que tentes contestar, xunto co hexágono de 37 hexágonos:

Até agora construímos poliminos con polígonos regulares, pero non é esta a única posibilidade. Traémosche outro, formado por triángulos rectilíneos isósceles:

Dado que neste caso a hipotenusa e os catetos son diferentes, as hipotenusas asócianse con hipotenus e os catetos con catetos. Esta é a razón pola que hai máis dun dominou. Nótese que este triángulo perdeu a simetría dos polígonos regulares.

As pezas que se crean con leste mino son:

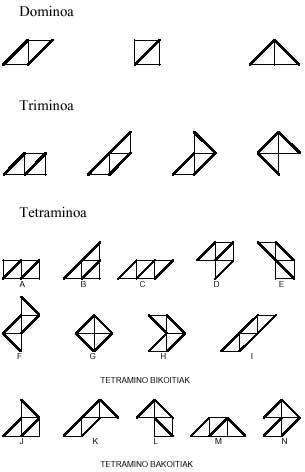
Deixámolo aquí de momento. Só imos dicir dúas cousas: Hai 30 pentaminos e 107 hexaminos.

Se a superficie de cada triángulo é a, a superficie de todos os dominios será 6 e non se poderá formar un cadro de superficie 6. A superficie dos triminos é de 12 e non se pode formar cadrada. Outro tanto ocorre cos tetraminos, cunha superficie total de 56. Con todo, existen cadrados que poden formar parte do subconjunto do sistema de tetraminas completo. Paira iso só tes que mirar a seguinte imaxe.

Como podes ver na seguinte imaxe, os cadros son de dous tipos: uno coa parte do cadro formada por hipotenus e o outro coa parte encadeada.

Ademais dos cadrados pódense construír rectángulos, entre os que tamén se poden distinguir os dous tipos anteriores. Na imaxe seguinte pódense ver os rectángulos de ambos os tipos. En ambos os casos hai exemplos de rectángulos formados por varias pezas. Os rectángulos grises deberían formarse con 14 tetraminas, o que non é posible. Esta afirmación non é gratuíta, xa que a incapacidade está demostrada. A clasificación dos tetraminas está relacionada con esta demostración.

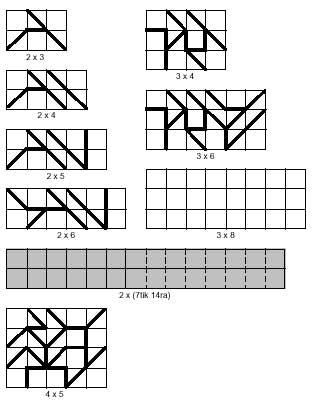
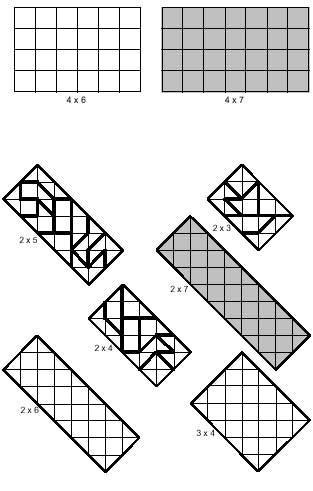
Os tetraminos pares presentan un número par de hipotenusas no límite exterior e en ambas as direccións. Pola contra, os tetraminos impares teñen un número impar en ambas as direccións. A demostración baséase precisamente en que paira completar o rectángulo é necesario que en ambas as direccións haxa un número par de hipótese. Con todo, hai cinco tetraminos impares, polo que isto non se pode encher se se queren coller os 14 tetraminos.

Os rectángulos brancos que aparecen na imaxe son para que tentes resolvelos.

Paira os valentes temos un traballo difícil. Descartando os tetraminos simétricos, podería formarse o cadro de superficie 16a outros 8 tetraminos (C,E,F,I,J,K,L,N)? (o lado desta casa estaría formado por 4 encadeados). E a segunda pregunta, tendo en conta as simétricas de 8 tetraminos non simétricos (é dicir, 16 tetraminos en total), pero agora non se lles pode dar a volta, poderíase completar o cadro favorable de 4 hipotenus?