Polymènes (II)

1990/02/01 Angulo, Patxi Iturria: Elhuyar aldizkaria

• Matematika

Dans le numéro précédent, nous avons parlé des polymines. Du mot “domino” nous sortons les mots trimino, tétramino, pentamino, hexamino et, en général, polyminum. On y obtenait les jeux de polyminum en identifiant deux mino, tels que trimino trois mino, tétramino -quatre mino, pentamino -cinq mino et hexamino -six minos. Dans tous nous acceptons l'équivalence mineure?

Dans ce numéro, nous allons élargir le concept de “mino” et, en plus du tableau, vous donner des significations de triangle équilatéral et hexagone. La raison en est que le seul polygone régulier qui peut former le plan soit celui des trois mentionnés, le carré, le triangle équilatéral et l'hexagone.

En commençant par les triangles équilatéraux et suivant le même développement, nous formerons des jeux triangulaires de domaines, trimins, tétramins, pentaminos et hexamins. Toutes les pièces de ces jeux sont:

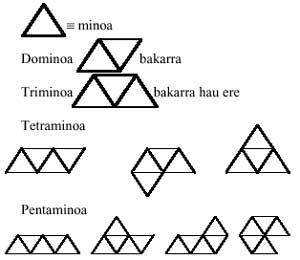
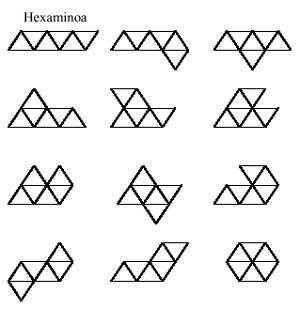
Une question nous vient en tête: Peut-on former des pentaminos avec des mèdes et des trimins ? Et puis une autre: Peut-on former des hexamins avec deux trimins ? Et un autre: Peut-on former des hexamins avec des dominos et des tétramins ? La réponse à la première est affirmative. Mais celui des autres non. Quels sont les examins qui ne peuvent former deux trimins? et ceux qui ne peuvent se former par l'union de domaines et de tétramins?

Les tétramins nous offrent une autre alternative, à savoir, peut-on dire que les tétramins sont des développements lisses du tétraèdre? Ou autrement dit, pouvez-vous compléter le tétraèdre avec des tétramins?

Voici trois images qui peuvent être constituées de portées triangulaires:

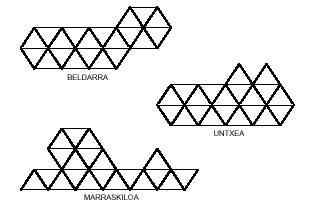
La réponse est que vous essayez de compléter douze hexamins.

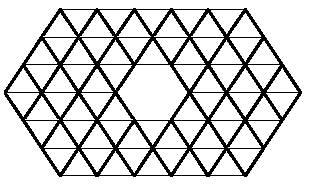
Nous laissons les polymères triangulaires avec ce dernier.

Avant d'aller de l'avant, bien sûr, la façon la plus simple de répondre aux questions soulevées ici est par l'élaboration de polyminos, que nous recommandons.

Passons maintenant aux polymères hexagonaux.

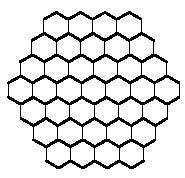
Les polymères hexagonales, comme il ne pouvait en être autrement, se composent d'hexagones, qui est ce que nous allons faire maintenant, en prenant au moins l'hexagone:

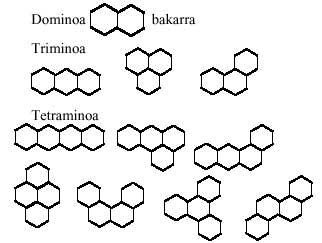
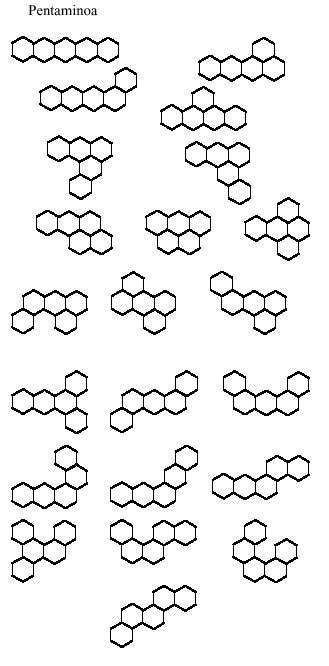
Les hexagonales ne sont pas apportées car il y a 82 hexamins différents. La vérité est que le nombre de portées (22) est assez grand pour jouer avec eux. Cependant, plus tard, nous vous proposons quelques images.

Pour compléter avec des tétramins hexagonales nous vous proposons les images suivantes (voir image ci-jointe), mais l'une des huit ne peut pas être complétée.

Vous devez le chercher vous. Sept tétramins seront nécessaires en tous.

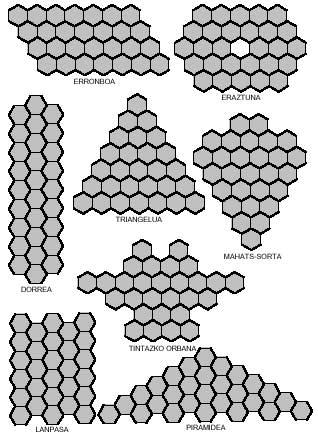
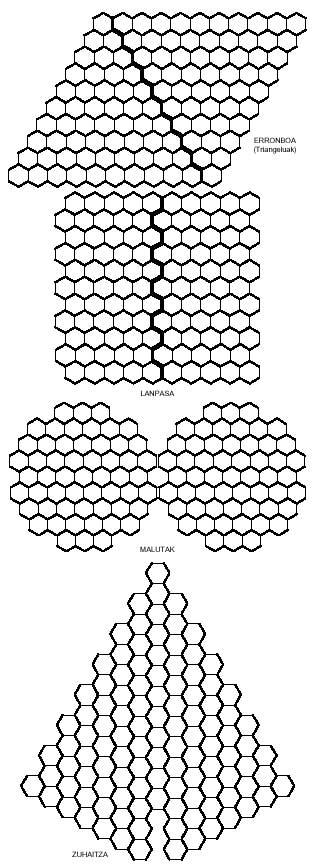
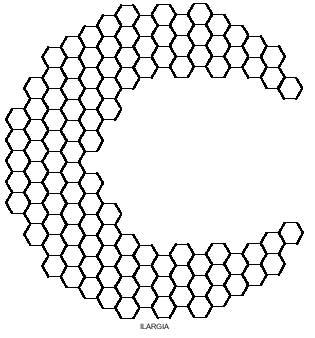
Vous pouvez également obtenir des images curieuses avec des portées hexagonales comme celles de la figure suivante. Quatre d'entre elles, comme on le voit, peuvent être divisées en deux parties, et dans les deux, dans le losange et dans le couloir, en plaçant les deux parties autrement, on peut obtenir des losanges et des lanpes plus longues.

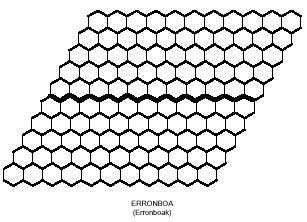
Comme nous essayions de former des rectangles avec des polymères carrés, avec les polymères hexagonales nous pourrions essayer de construire des hexagones. Les hexagones formés par des hexagones ont besoin de 1, 7, 19, 37, 61, 91, 127,… hexagones. Ces montants ne sont pas atteints par les trimins (9), ni par les tétramins (28) ni par les pentaminos (110). Mais si vous vous apercevez, l'union de trimino et de tétramino permet de former un hexagone de 37 hexagones. Mais peut-on vraiment compléter cet hexagone avec trois trimins et sept tétramins? Voici une autre question pour que vous essayiez de répondre, avec l'hexagone de 37 hexagones:

Jusqu'à présent, nous avons construit des polymines avec des polygones réguliers, mais ce n'est pas la seule possibilité. Nous vous apportons un autre, composé de triangles isocèle rectilignes:

Comme dans ce cas l'hypotense et les catètes sont différents, les hypotenses sont associées à l'hypotenus et les catètes avec des catètes. C'est pourquoi il ya plus d'un domino. Notez que ce triangle a perdu la symétrie des polygones réguliers.

Les pièces qui sont créés avec ce mino sont:

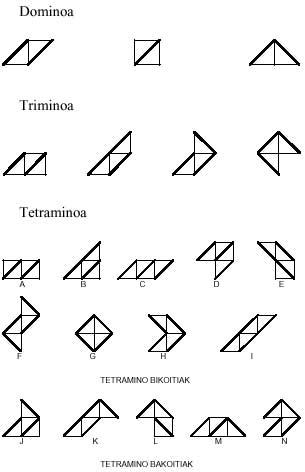
Nous le laissons ici pour le moment. Nous allons juste dire deux choses: Il y a 30 pentaminos et 107 hexamins.

Si la surface de chaque triangle est a, la surface de tous les domaines sera 6 et un bloc de surface 6 ne pourra pas être formé. La surface des trimins est de 12 et ne peut pas être formée carrée. Il en va de même pour les tétramins, avec une surface totale de 56. Cependant, il existe des carrés qui peuvent faire partie du sous-ensemble du système de tétramines complet. Pour ce faire, il suffit de regarder l'image suivante.

Comme vous pouvez le voir dans l'image suivante, les tableaux sont de deux types: l'un avec la partie du tableau formée par hipotenus et l'autre avec la partie enchaînée.

En plus des carrés, vous pouvez construire des rectangles, parmi lesquels vous pouvez également distinguer les deux types ci-dessus. Dans l'image suivante, vous pouvez voir les rectangles des deux types. Dans les deux cas, il existe des exemples de rectangles formés par plusieurs pièces. Les rectangles gris devraient être formés avec 14 tétramines, ce qui n'est pas possible. Cette affirmation n'est pas gratuite, car l'incapacité est démontrée. La classification des tétramines est liée à cette démonstration.

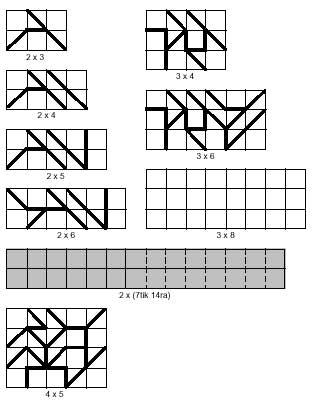
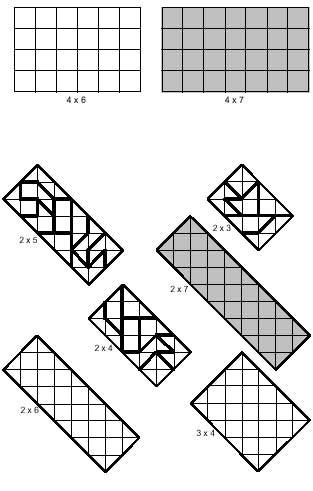
Les tétramins paires présentent un nombre pair d'hypotenseurs dans la limite extérieure et dans les deux directions. En revanche, les tétramins impaires ont un nombre impair dans les deux sens. La démonstration repose précisément sur le fait que pour compléter le rectangle il est nécessaire que dans les deux sens il y ait un nombre pair d'hypothèses. Cependant, il ya cinq tétramins impaires, de sorte que cela ne peut pas être rempli si vous voulez attraper les 14 tétramins.

Les rectangles blancs qui apparaissent dans l'image sont pour que vous essayiez de les résoudre.

Pour les courageux, nous avons un travail difficile. En écartant les tétramins symétriques, le tableau de surface 16e pourrait-il être formé par 8 autres tétramins (C,E,F,I,J,K,L,N) ? (le côté de cette case serait composé de 4 enchaînés). Et la deuxième question, compte tenu des symétriques de 8 tétramins non symétriques (c'est à dire 16 tétramins au total), mais maintenant vous ne pouvez pas les retourner, pourrait-on compléter le tableau favorable de 4 hypotenus?