Poliminos (II)

1990/02/01 Angulo, Patxi Iturria: Elhuyar aldizkaria

• Matematika

En el número anterior hablamos de los poliminos. De la palabra “domino” sacamos las palabras trimino, tetramino, pentamino, hexamino y, en general, polimino. En ella obteníamos los juegos de polimino identificando dos mino, tales como trimino>tres mino, tetramino -cuatro mino, pentamino -cinco mino y hexamino -seis minos. En todos ellos aceptamos la equivalencia mino?

En este número ampliaremos el concepto de “mino” y, además del cuadro, le daremos significados de triángulo equilátero y hexágono. La razón es que el único polígono regular que puede formar el plano sea el de los tres mencionados, el cuadrado, el triángulo equilátero y el hexágono.

Comenzando con los triángulos equiláteros y siguiendo el mismo desarrollo, formaremos juegos triangulares de dominios, triminos, tetraminos, pentaminos y hexaminos. Todas las piezas de estos juegos son:

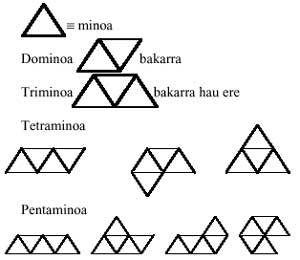
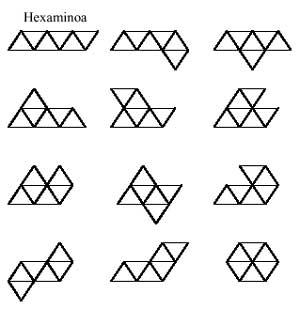
Nos viene a la cabeza una pregunta: ¿se pueden formar pentaminos con medos y triminos? Y después otra: ¿y se pueden formar hexaminos con dos triminos?. Y otro: ¿se pueden formar hexaminos con dominos y tetraminos?. La respuesta a la primera es afirmativa. Pero el de los demás no. ¿Cuáles son los examinos que no pueden formar dos triminos? ¿y los que no pueden formarse mediante la unión de dominios y tetraminos?

Los tetraminos nos ofrecen otra alternativa, es decir, ¿se puede decir que los tetraminos son desarrollos lisos del tetraedro?. O dicho de otro modo, ¿se puede completar el tetraedro con tetraminos?

A continuación se presentan tres imágenes que pueden estar formadas por pentaminos triangulares:

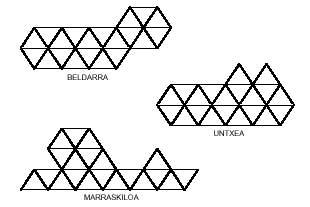
La respuesta es para que intentes completar doce hexaminos.

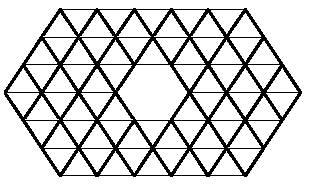
Dejamos los polímeros triangulares con este último.

Antes de seguir adelante, por supuesto, la forma más sencilla de responder a las preguntas aquí planteadas es a través de la elaboración de poliminos, que te recomendamos.

Pasemos ahora a los polímeros hexagonales.

Los polímeros hexagonales, como no podía ser de otra manera, se componen de hexágonos, que es lo que vamos a hacer ahora, tomando como mínimo el hexágono:

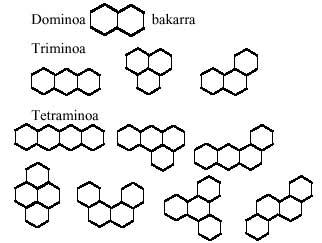
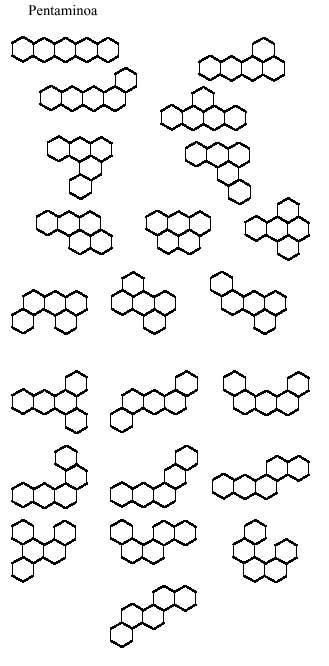
Los hexagonales no se traen ya que hay 82 hexaminos diferentes. La verdad es que el número de pentaminos (22) queda bastante grande para jugar con ellos. Sin embargo, más adelante te proponemos algunas imágenes.

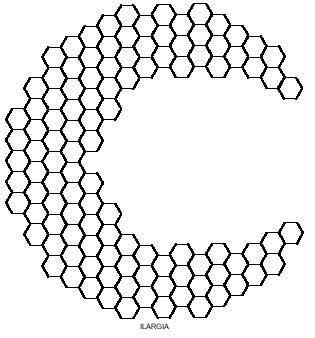
Para completar con tetraminos hexagonales te proponemos las siguientes imágenes (ver imagen adjunta), pero una de las ocho no se puede completar.

Tienes que buscarlo tú. En todos ellos serán necesarios siete tetraminos.

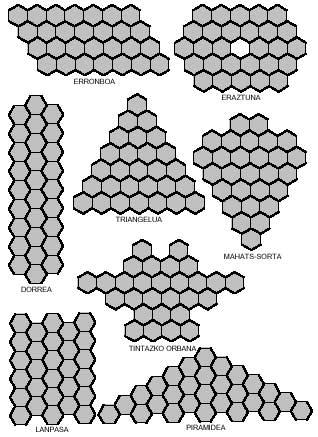
También se pueden obtener imágenes curiosas con pentaminos hexagonales como los de la siguiente figura. Cuatro de ellas, como se ve, se pueden dividir en dos partes, y en ambas, en el rombo y en el pasillo, colocando las dos partes de otra manera, se pueden conseguir rombos y lanpas más largos.

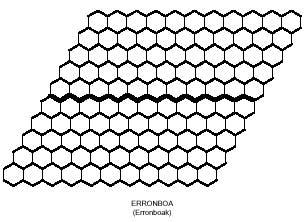
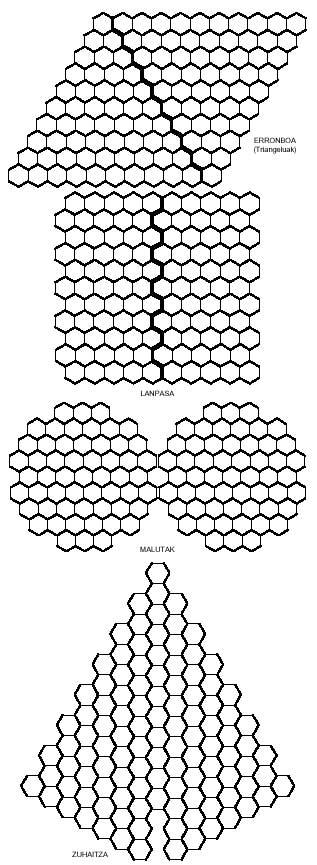
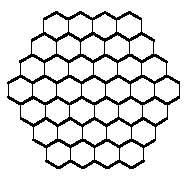
Al igual que tratábamos de formar rectángulos con polímeros cuadrados, con los polímeros hexagonales podríamos intentar construir hexágonos. Los hexágonos formados por hexágonos necesitan 1, 7, 19, 37, 61, 91, 127,… hexágonos. Estas cantidades no son alcanzadas por los triminos (9), ni por los tetraminos (28) ni por los pentaminos (110). Pero si os percatáis, la unión de trimino y tetramino permite formar un hexágono de 37 hexágonos. Pero ¿realmente se puede completar dicho hexágono con tres triminos y siete tetraminos? Ahí tienes otra pregunta para que intentes contestar, junto con el hexágono de 37 hexágonos:

Hasta ahora hemos construido poliminos con polígonos regulares, pero no es ésta la única posibilidad. Te traemos otro, formado por triángulos rectilíneos isósceles:

Dado que en este caso la hipotenusa y los catetos son diferentes, las hipotenusas se asocian con hipotenus y los catetos con catetos. Esta es la razón por la que hay más de un dominó. Nótese que este triángulo ha perdido la simetría de los polígonos regulares.

Las piezas que se crean con este mino son:

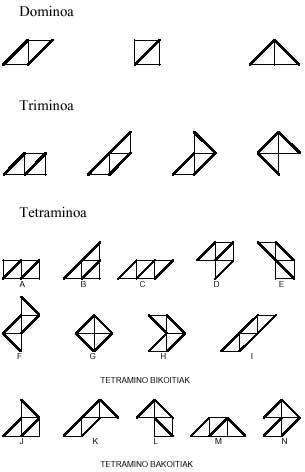
Lo dejamos aquí de momento. Sólo vamos a decir dos cosas: Hay 30 pentaminos y 107 hexaminos.

Si la superficie de cada triángulo es a, la superficie de todos los dominios será 6 y no se podrá formar un cuadro de superficie 6. La superficie de los triminos es de 12 y no se puede formar cuadrada. Otro tanto ocurre con los tetraminos, con una superficie total de 56. Sin embargo, existen cuadrados que pueden formar parte del subconjunto del sistema de tetraminas completo. Para ello sólo tienes que mirar la siguiente imagen.

Como puedes ver en la siguiente imagen, los cuadros son de dos tipos: uno con la parte del cuadro formada por hipotenus y el otro con la parte encadenada.

Además de los cuadrados se pueden construir rectángulos, entre los que también se pueden distinguir los dos tipos anteriores. En la imagen siguiente se pueden ver los rectángulos de ambos tipos. En ambos casos hay ejemplos de rectángulos formados por varias piezas. Los rectángulos grises deberían formarse con 14 tetraminas, lo que no es posible. Esta afirmación no es gratuita, ya que la incapacidad está demostrada. La clasificación de los tetraminas está relacionada con esta demostración.

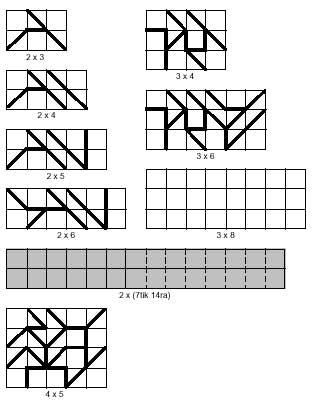
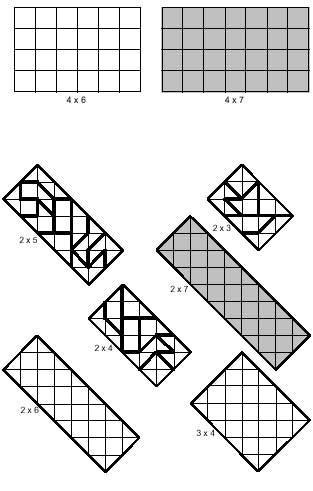
Los tetraminos pares presentan un número par de hipotenusas en el límite exterior y en ambas direcciones. Por el contrario, los tetraminos impares tienen un número impar en ambas direcciones. La demostración se basa precisamente en que para completar el rectángulo es necesario que en ambas direcciones haya un número par de hipótesis. Sin embargo, hay cinco tetraminos impares, por lo que esto no se puede llenar si se quieren coger los 14 tetraminos.

Los rectángulos blancos que aparecen en la imagen son para que intentes resolverlos.

Para los valientes tenemos un trabajo difícil. Descartando los tetraminos simétricos, ¿podría formarse el cuadro de superficie 16a otros 8 tetraminos (C,E,F,I,J,K,L,N)? (el lado de esta casilla estaría formado por 4 encadenados). Y la segunda pregunta, teniendo en cuenta las simétricas de 8 tetraminos no simétricos (es decir, 16 tetraminos en total), pero ahora no se les puede dar la vuelta, ¿se podría completar el cuadro favorable de 4 hipotenus?