How to convert the rectangle to square?

1985/12/01 Goñi, Jesus Mari | Etxeberria, J. Iturria: Elhuyar aldizkaria

• Matematika

The way forward to find the answer is divided into several stages.

At the foot of a rectangle: if we call and at height the value of a surface b will be given by the formula axb. Then, the value to be given on each side to form a square with that surface will be a.b.
• Therefore, we have moved from the problem we had before to a new problem. If values a and b are known, how to complete the value a.b.

Let's try.

Figure 1:

OA=1 unit AB = value a (with compass) OA'=b (with compass) A'B'= x AB and A'B' are perpendicular to the OM line

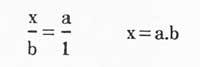
Next:

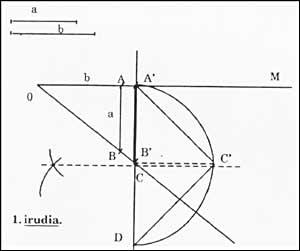
B'D = unit C, midpoint of segment A'D with center A'C'D in C B'C', perpendicular to line A'D' from B'C', being the height of the right triangle A'C'D = B'C' A'B'

B'C'= a.b

That was the value we were looking for.

It is enough, therefore, to repeat the work we have done to convert a rectangle into square, replacing the generals a and b with the foot and the concrete heights of that rectangle. Then using the B'C' segment as side, to complete the square.

This evolution is interesting in itself, but the most interesting thing is how easy it is to rectify other polygons. Thus, the rectangle plays the role of mediator.

Squaring a polygon, that is, turning it into a square equivalent to the surface, is not easy if we want to do it in a correct way, but if we use the rectangle as an intermediate auxiliary element everything is easier.

As the square a polygon and calculate its surface are equivalent, the interest of this operation seems evident.

In this issue, changing a little theme, we want to propose a new game.

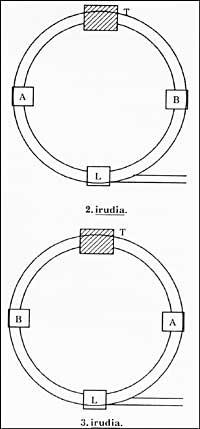
A and B are wagons of a train. L, the locomotive. T is a tunnel. Along this tunnel you can reach a locomotive but without cars.

The double line in Figure 2 is the railroad.

The essence of the game is how to move from the situation that appears in figure 2 to the one that appears in figure 3 moving as little as possible the locomotive?