Noetherren teoremarik politena
2019/12/01 Urizar Lanz, Iñigo - Fisikan doktorea Iturria: Elhuyar aldizkaria
Matematikariek Noetherren teorema bat baino gehiago ezagutzen dute. Izan ere, matematikarien familia ospetsu batek darama Noether abizena. Baina, denen artean, badago Noetherren teorema bereziki polit bat. Emmy Noetherrena da.
Amalie Emmy Noether 1882an jaio zen Alemanian. Askoren ustez, historiako emakume matematikaririk handiena izan da. Zailtasunak zailtasun, matematika ikastea lortu zuen (garai hartako emakumeentzako debekatuta baitzegoen); irakasle izatea ere debekatuta izanik, David Hilbert bere lagunaren ordez eman izan zituen eskolak. Einsteinen hitzetan, Noether matematikaren jeniorik handiena da, emakumeen goi-irakaskuntza hasi zenetik. 1918an, bere teoremarik ospetsuena argitaratu zuen Noetherrek. Aditu askoren ustez, fisika matematikoak daukan teoremarik eder eta sakonena.
Ederra da, aspaldidanik ezagutzen ziren kontserbazio-printzipioen oinarria erakusten digulako, printzipio ezberdin askok oinarri bera daukatela ikusarazten. Eta sakona, hasiera batean oso ezberdinak ematen duten bi ideia bateratzen dituelako: simetria- eta kontserbazio-printzipioak.
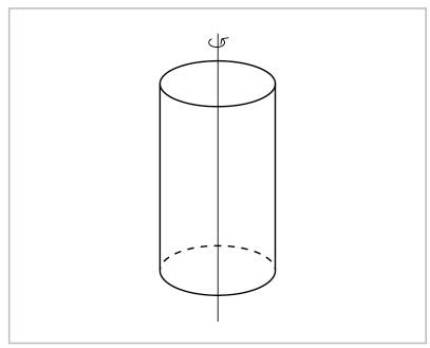
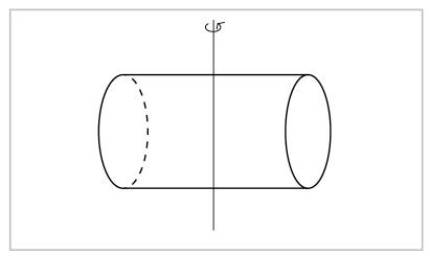
Simetriaren ideia oso oinarrizkoa da: simetria daukan gauza bat berdin ikusten dugu simetria-ariketa egin aurretik eta ondoren. Zilindro bat, esate baterako, berdin ikusiko dugu bere ardatzaren inguruan errotazio bat, edozein, eraginez gero. Ezin ditugu bereizi errotazioa eragin aurreko zilindroa eta ondorengoa.
Beste ardatz baten inguruan birarazten badugu, aldiz, zilindroa ez dugu berdin ikusiko. Jakin dezakegu norbaitek birarazi duen ala ez.
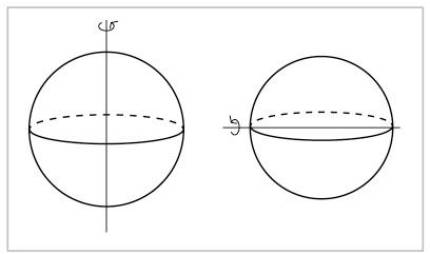
Esfera bat objektu are simetrikoagoa da. Haren zentrotik pasatzen den edozein ardatzen inguruan biraraziz gero, berdin ikusiko dugu.
Bi simetria-mota aipatu behar ditugu: simetria jarraituak eta simetria diskretoak. Matematikan, jarraitu hitzak zera esan nahi du: jarraitu den horren bi objektu bata bestearengandik nahi bezain gertu egon daitezke. Beraz, simetria jarraitu batean, bi simetria-eragiketa elkarrekiko oso-oso gertu daude. Esferaren eta zilindroaren ardatzen kasuetan, errotazio guztiak dira simetria, oso-oso txikiak badira ere. Eta simetria-eragiketa batetik oso-oso gertu bada beste simetria-eragiketa bat. Bigarren irudian, errotazio bat simetria izateko 180 gradukoa behar du izan; beraz, simetriako errotazio batetik oso gertu ez dago beste simetriako errotazio bat. Simetria hori diskretoa da.
Kontserbazio-printzipio batek, bestalde, esaten digu magnitude fisiko baten balioa ez dela aldatzen. Denok entzun dugu inoiz energiaren kontserbazioaren printzipioa: energia ezin da sortu ezta deuseztatu ere. Sistema fisiko batean, energia (baldin eta isolatuta badago) ez da denborarekin aldatzen. Beste kontserbazio-printzipio asko ere ezagutzen ziren XX. mendearen hasieran: momentu linealaren kontserbazio-printzipioa eta momentu angeluarraren kontserbazio-printzipioa, garrantzitsuenak aipatzearren.
Fisikariek holako printzipioak bilatzen dituzte euren sistemak hobeto ulertzen laguntzen dietelako. Adibidez, energiaren kontserbazio-printzipioari esker, gai gara azaltzeko zergatik doazen azkarrago planetak, eguzkiaren inguruan egiten duten elipsean, eguzkitik gertuago daudenean, urrunago daudenean baino (azalpena ematen dio, beraz, printzipio horrek Keplerren lege famatuari). Eta, hori gutxi balitz, gai gara asmatzeko zenbateko abiadura izango duten planetek puntu batean eta bestean. Antzerako gauza bat gertatzen zaigu atomoekin: gai gara jakiteko zer koloretako argia igorriko duen espezie kimiko jakin bateko atomo batek, energiaren kontserbazio-printzipioari so eginez, besterik gabe.
Momentu linealaren kontserbazio-printzipioari esker, gai gara jakiteko talka baten ondoren zer abiadurarekin irtengo diren talka egin duten objektuak. Hori erabil dezakegu, adibidez, zirkulazio-istripu batean ibilgailuek zer abiadura zeukaten jakiteko, edo Higgsen bosoia sortu zuen talkaren zehaztasunak kontrolatzeko.
Momentu angeluarraren kontserbazioak, azkenik, ondorio polit hau dauka (beste askoren artean): planeta batek eguzkiaren inguruan egiten duen orbita plano batean dago. Hau da, planeta bat ezin da sekula plano horretatik atera. Lurraren orbitaren planoari ekliptika deitzen zaio. Astronomiazaleei ezagun izango zaie hitz hori, eguzkiak zeruan egiten duen ibilbidearen izena ere badelako, eta zodiakoko konstelazioak bertan kokatuta daudelako. Bada, momentu angeluarraren kontserbazio-printzipioagatik ez balitz, Lurraren orbita ez litzateke ekliptikan egongo, eta plano horretatik gora eta behera ibiliko litzateke, planotik irteten.
XX. mendearen hasieran holako kontserbazio-printzipio batzuk ezagutzen ziren. Garai hartan, Noetherrek esanahi harrigarri bat eman zien printzipio haiei. Haren teoremaren bertsio informal bat enuntziatuko dugu:
“Sistema bateko edozein simetria jarraituri kontserbazio-printzipio bat dagokio”.
Teoremaren frogapena eman zuen Noetherrek (artikulu honetan ez dugu emango, oso teknikoa baita). Esaldi horren esanahia eta sakonera hobeto ulertzeko, jar ditzagun adibide moduan fisikako simetriarik garrantzitsuenak: espazio-denboraren simetriak.
Hasi baino lehen, zer da espazio-denboraren simetria bat? Bada, imajina dezagun espazio hutsa. Izarren arteko espazioa, nahi badugu, non ez dagoen grabitaterik. Zer aldaketa geometriko egin diezaiokegu espazio horri? Bada, adibidez, espazioan translazio bat egin dezakegu. Hau da, edozein norabidetan mugi gaitezke distantzia jakin batez. Fisikan badago printzipio bat, erlatibitatearen printzipio deritzona, esaten diguna fisikaren lege denek berdin-berdinak izan behar dutela gure posizio berri honetan. Berdinak ez balira, esperimentu baten emaitza ezberdina izango litzateke posizio batean edo bestean. Adibidez, atomo baten elektroiak era ezberdin batean kokatuko lirateke gure gelan, gure auzokidearen etxean edo Andromeda galaxian. Ez dugu holakorik ikusi sekula; beraz, pentsatzen dugu fisikaren legeak berdinak direla espazioko puntu denetan, eta beraz esperimentu guztien emaitzak berdinak direla edozein tokitan eginda ere. Horregatik esaten dugu hori espazioaren simetria bat dela, espazioko puntu bat ezin delako beste guztietatik bereizi.
Erlatibitatearen printzipioak ematen digu beste simetria batzuen berri: sekula inork ez du ikusi denborarekin aldatzen den fisikaren legerik. Elektrizitatearen legeak, esate baterako, XIX. mendean ezarri ziren, eta gaur egun berdin-berdinak izaten jarraitzen dute (Maxwellen lege esaten zaie). Ez dira aldatu. Are gehiago, arrazoi boteretsuak dauzkagu pentsatzeko iraganean ere hainbat miloi urtez izan direla egia lege horiek. Fenomeno horri denbora-translazioekiko simetria deitzen zaio. Iraganerako edo etorkizunerako denbora-translazio batek ezin du fisikaren legerik aldatu. Esperimentu baten emaitza bera izango da gaur, atzo edo bihar.
Badauzkagu, beraz, erlatibitatearen printzipioak eman dizkigun bi simetria: espazio-translazioak eta denbora-translazioak. Badago hirugarren simetria bat erlatibitatearen printzipioak ematen diguna: errotazioekiko simetria. Fisikaren lege guztiak berdinak dira sistema osoa hartu eta birarazi egingo bagenu. Hau da, espazioak ez dauka norabide pribilegiaturik, zeinari begira egonez gero fisika ezberdin bat ikusten den beste norabide guztiekin alderatuta.
Beraz, erlatibitatearen printzipioaren arabera, espazioak ez dauka toki pribilegiaturik, ez dauka une pribilegiaturik eta ez dauka norabide pribilegiaturik. Esperimentu ororen emaitza (adibidez, bi elektroiren arteko talka edo protoi bat osatzen duten hiru quarken egoera) berdin-berdina da espazioko puntu guztietan, denborako une guztietan eta espazioko norabide guztietan. Begiak itxiko bagenitu eta errotazio bat, denbora-translazio bat edo espazio-translazio bat egingo bagenu, berriro irekitzean ezingo genuke inolaz ere jakin eragiketa hori gertatu den ala ez. Horiexek dira erlatibitatearen printzipioak ezartzen dituen espazio-denboraren simetriak (izan ere, erlatibitatearen printzipioak simetria gehiagoren berri ematen digu, baina ez ditugu artikulu honetan aipatuko, gauzak gehiegi ez nahastearren).
Hiru simetria horiek jarraituak dira. Espazio-translazioen kasuan, oso translazio txikia egin dezakegu eta oso puntu hurbil batean gera gaitezke. Denbora-translazioen kasuan ere, oso une hurbil batera ”mugi” gaitezke (espazioan eta denboran jauzi ez-jarraiturik ez dago). Eta ardatz bat aukeratuta, oso errotazio txiki bat egin dezakegu haren inguruan. Beraz, simetria jarraituak izanik, Noetherren teorema aplika dakieke.
Eta zeintzuk izango lirateke simetria horiei dagozkien magnitude kontserbatuak? Bada, teoremak berak hau ere esaten digu: espazio-translazioen kasuan, kontserbatzen den magnitudea momentu lineala da. Denbora-translazioen kasuan, energia. Eta errotazioen kasuan, momentu angeluarra. Hau emaitza polita!
Noetherrek oso lotura sakona eta harrigarria aurkitu zuen simetrien eta kontserbazio-printzipioen artean: bata bestearen ondorioa dira! Biak batera doaz, ezin dira elkarrengandik bereizi. Energia kontserbatuko ez litzatekeen mundu batean, denborarekin garatuko lirateke fisikaren legeak, hau da, denboran aldatzen joango lirateke. Denborako bi une ezberdin ez lirateke bereizezinak izango.
Artikulu honetan aipatu ez baditugu ere (espazio-denboraren simetriei buruz baino ez baitugu hitz egin), beste simetria guztiei aplika dakieke teorema hau. Irakurle ikusnahien jakin-mina pizteko, esango dugu karga elektrikoaren kontserbazioa ere Noetherren teoremaren ondorioa dela. Kasu horretan, simetria ez dauka espazio-denborak, baizik eta ekuazioen sistemak berak, eta simetria abstraktuago horri gauge simetria deitzen zaio. Horrek interpretazio geometriko bat ere izan dezake, lau dimentsio baino gehiago dauzkan espazio batean. Baina hori... beste egun baterako uzteko kontua da.
Robert Waldek esan zuen bezala, horretaz konturatu eta gero, batek ezin du saihestu sentitzea gauza oso sakon bat ikasi duela naturak jarduteko duen moduari buruz. Horixe da, beraz, emakume handi honek utzi zigun opari polita.
Bibliografia

Gai honi buruzko eduki gehiago
Elhuyarrek garatutako teknologia