Nikolai I. Lobatxevski (1792-1856): Ezerezetik mundu berria

Matematikaren historian gutxitan izan da Geometria ez-euklidearra aurkitzeak ekarri zuen astindua bezalakorik. Oinarri-oinarrietan krisia ezartzen zuen, baina ohi bezala, krisitik indartuta atera zen, bide berrietan barrena abiatzeko moduan. Geometria ez-euklidearraren sortzaile gisa izen bi aipatzen dira nagusiki: Nikolai Lobatxevski errusiarra eta János Bolyai hungariarra. Mendeurren famatuetako ospakizunen artean joan zaigun 1992. urteak beste batzuk ezkutaturik utzi dizkigu eta hauetariko bat Lobatxevskiren jaiotzaren bigarrena da.

Euklides eta bostgarren postulatua

Alexandriako Euklidesen "Elementuak" liburuaren latinezko bertsioaren orri bat. K. a. hirugarren mendean greziarrek matematikaren historiarako eskaini ziguten lehenengo liburua da.

K. a. hirugarren mendean eskaini ziguten greziarrek Matematikaren historiarako gelditu den lehenengo liburua: Alexandriako Euklidesen Elementuak, alegia. Bertan zenbakiak eta Geometria dira aztergai nagusi. Gaia ezezik, metodoa da garrantzizkoa; Matematikan erabiltzen den metodo axiomatiko-deduktiboaren oinarria bertan baitago. Hasteko, aldez aurretik ontzat ematen eta frogatu behar ez diren baieztapenak daude (postulatuak edo axiomak). Gero, Logikaren erregelak aplikatuz beste baieztapen batzuk (proposizioak edo teoremak) frogatzen dira.

Zein baldintza eskatu behar zaie postulatuei teoria bat eraiki nahi denean? Alde batetik, behar-beharrezkoa da kontraesankorrak ez izatea (hots, emaitza bat eta bere aurkakoa ez ondorioztatzea). Bestetik, komeni da gehiegi ez izatea, nahiz eta honek teoria hondatuko ez lukeen. Noiz dira gehiegi? Postulatu bat besteen ondorio denean, postulatuen zerrendatik kendu eta teorema modura ager daiteke, teoria osoa aldatzeke gelditzen delarik.

Euklidesek bost postulatu berezi erabili zituen Geometriarako. Elementuak-en fomulazioa geometrikoagoa den arren, hitz lauz honela defini daitezke:

1. Bi edozein puntu desberdinetatik zuzen bakar bat pasatzen da.
   
2. Bi edozein zuzenki emanda, lehenengoaren alboan bigarrenarekin kongruente den beste bat jar daiteke, zuzenki luzeagoa emateko.
   
3. Bi edozein puntu desberdin emanda, beti dago lehenengoa zentrutzat duen eta bigarrenetik pasatzen den zirkunferentzia.
   
4. Angelu zuzen guztiak kongruenteak dira.
   
5. Zuzen batek beste bi zuzen ebakitzen baditu eta alde bateko barne-angeluen batura bi angeluzuzen baino txikiagoa bada, alde horretara zuzenak luzatuz elkartu egingo dira.

Lehenengo lau postulatuek zalantza handirik gabe onartzekoak diruditen arren, bostgarrena berezia dela sumatu zen aspaldidanik. Euklidesen lanean ere honen itxurako zerbait nabaritzen da (lehenbiziko 28 proposizioak delako postulatu hori erabili gabe frogatu baitzituen eta ezinbestekoa izan zitzaionean baino ez baitzuen sartu).

Ondorengo mendeetan matematikari asko eta asko arduratu da bostgarren postulatuaz eta jarrera bi finka daitezke: batzuek, Euklidesen formulazioa oso gustora hartu ez eta beste formulazio “onargarriago” batez ordezkatu zuten. Beste batzuk, ordea, bostgarren postulatua beste lauen ondorio zela frogatzen saiatu ziren. Hauetariko askok “frogapena” eman zuten, baina beti nahi gabe besteen taldera pasatuz, hau da, konturatu gabe ordezko postulatu bat erabiliz. Geometria euklidearraren ohizko liburu eta kurtsoetan, ordezko postulatuen artean batek hartu zion tokia Euklides-ek eman zuenari: Zuzen baten kanpoko puntu batetik zuzen paralelo bakarra egin dakioke. Honexegatik deitzen zaio bostgarrenari paraleloen postulatua.

Beltrami-Klein-en eredua. Zuzenak, zirkulu barruko zuzenkiak dira.

Bostgarren postulatua (edozein formulaziotan) aurrekoen ondorio dela ikusteko bide bat absurdura eramatea litzateke: aurkakoa egia dela kontsideratuz, kontraesan batera heldu. XIX. mendea baino lehen bide honetan aurreratuenak Gerolamo Saccheri (1677-1733) jesuita italiarra eta Johann Heinrich Lambert (1728-1777) suitzarra izan ziren. Saccherik emaitza interesgarriak baina itxura arraro samarrekoak aurkitu zituen (Geometria euklidearrak ohituta gauzkan emaitzekin konparatuz, noski).

Hauetariko bat ezinezkotzat jo eta horrekin paraleloen postulatua zuzena dela ondorioztatu zuen, Euklides akats guztietatik garbi izeneko liburuan erakutsi zigunez. Lambertek, besteak beste, Saccheri ez zela kontraesanera heldu azpimarratu zuen eta bere aldetik emaitza gehiago lortu zituela ere bai. Gainera bostgarren postulatua besteen ondorio gisa ezin zitekeela lortu sumatu zuen eta aurkakoak ematen dituen emaitzak ohizko esperientziatik begiratuta arraroak izan daitezkeela, baina Logikaren ikuspegitik kontraesankorrak inola ere ez. Paraleloen postulatua onartzeko arrazoi bakarra komenientzia litzateke, beraz. Horri esker, Lambert hurrengo mendeko lanen aitzindari izan zen.

XVIII. mendearen bukaeran, bestalde, Kant filosofo ospetsuaren iritziak ere eragin handia izan zuen eztabaidan. Kanten iritziz ezin daiteke euklidearra ez den beste Geometriarik asmatu; aldez aurretik (a priori) daukagun ezagutza baita.

Lobatxevskiren ekarpena

Beste askorenak bezala Lobatxevskik lehen pausoak, paraleloen postulatua frogatzeko asmoz eman zituen eta lortu zuela ere uste izan zuen. Handik laster, ordea, beste bide bat hartu zuen. Bostgarren postulatua esperientziak “frogatzen” zuela esaten zuen eta ez dagoela hortik kanpoko frogapena ematerik, edo bestela esan, ez dela lehen lau postulatuen ondorio. Are gehiago, beste lau postulatuak gordeta posible izan beharko luke horren ordez beste postulatu (ez baliokide) bat jartzeak eta euklidearra ez den beste Geometria bat eraikitzeak, hau ere kontraesanik gabea izanik. Lehenago aipatu dugun Lamberten ildotik badoa ere, badirudi Lobatxevskik ez zuela haren lanen berri.

Berak proposatu zuen ordezko postulatua hauxe zen: zuzen baten kanpoko puntu batetik zuzen desberdin bi egin daitezke lehengoarekin elkartzen direnak. “Gainazal eta lerroak ez daude Naturan; irudimenean baizik” esango du, argi eta garbi Geometria mundu fisikotik at utziz (beste kontu bat da Fisikaren beharrei zein Geometria komeni zaion). Hasieran Geometria irudikaria hitzez izendatu zuen asmazio hori eta, geroago, Pangeometria izenez. Gaur egun Geometria hiperbolikoa esaten zaio (Lobatxevskiren Geometria ere bai batzuetan). Geometria honetan frogatzen diren teoremak, lehenago aipatu dugunez, ez dira ohizkoak. Hona hemen adibide-pare bat:

• Triangelu baten angeluen batura bi angeluzuzen baino txikiagoa da eta bere azalera, batura horri bi angeluzuzen izateko falta zaionarekiko proportzionala.
  
• Bi triangeluren angeluak berdinak badira, triangeluak berdinak dira.

Gauss. Gaussen proposamena izan omen zen Lobatxevski Göttingengo Zientzi Elkarteko partaide izendatzea.

Lobatxevskik Geometria honi dagokion Trigonometria ere eraiki zuen; hau ere ohizkotik desberdina, noski. Baina bien artean erlazioak badaude eta elkar sostengatzen dute, hots, bata posible bada bestea ere bai.

Nahiz eta beste arlo batzuetan ere lan egin, Geometri lanengatik da ezaguna Lobatxevski. 1826. urteko otsailean hitz egin omen zuen lehen aldiz jendaurrean bere ideia berriez eta 1829.ean eman zuen argitara lehen gai horretaz Kazango Buletinean. Honen ondoren beste batzuk etorri ziren, beti errusieraz, 1837.ean Journal de Crelle famatuan lan bat frantsesez atera zuen arte (Geometria Irudikaria izenburupean) eta hiru urte geroago monografia bat alemanez (Ikerketa Geometrikoak Paraleloen Teoriaz). Hil baino urtebete lehenago azalpen osoa argitaratu zuen Pangeometria izenburuaz, bai errusieraz eta bai frantsesez.

Bolyai eta Gauss

Lobatxevski ez zen ondorio horietara heldutako bakarra izan. János Bolyai (1802-1860) hungariarrak bere aita Wolfgang Bolyairen Tentamen Juventutem Studiosam in Elementa Mathesis (1832-33) izeneko liburuaren eraskin gisa eman zuen “Espazio Absolutuaren Zientzia” lana, Lobatxevskiren lanaren oso antzekoa da. Bolyai gazteak 1823.ean aitari bere lanen berri eman zionean, honela esan zion eskutitz batean: “Hain aurkikuntza liluragarriak egin ditut, non neu ere harriduraz galduta bainago: ezerezetik mundu berri desberdina sortu dut’. Wolfgang Bolyai Gaussen laguna zen eta garai hartan berau zen matematikaririk famatuena. Horregatik semearen lana bidali zion iritzia eman ziezaion.

Hona Gaussen erantzuna: “Lan hau ezin dudala goraipatu esanez hasten banaiz, harritu egingo zara, baina ezin dut besterik egin, neure burua goraipatuko bainuke, lanaren edukin osoa, zure semeak hartu duen bidea eta lortu nahi dituen emaitzak ia osorik azken 30-35 urteotan egin ditudan gogoetekin bat datozelako”. Min hartu zuen Bolyai gazteak hitz hauek entzunda, Gaussek bere emaitzak lapurtu egin nahi zizkiolakoan. Bestalde, Lobatxevskiren lana ikusita ere, hasiera batean behintzat, bere lanetik kopiatuta zegoela uste izan zuen. Horren ondorioz Matematika utzi egin zuen betirako. Baina kopiatu gabe ere ikerlari desberdinengandik antzeko emaitzak lortzea ez da hain arraroa. Oso adierazgarri dira Wolfgang Bolyairen hitz hauek: “Badirudi ondorio batzuetara leku askotatik hel daitekeela, non zenbait leku desberdinetan aurkitzen diren (gertatu zen moduan), udaberrian bioletak nonnahi agertzen diren bezala”.

Gaussek Geometria ez-euklidearrez egindako lana ez da ondo ezagutzen; itxuraz filosofo kantiarren kontrako erreakzioa segurutzat jotzen zuelako ez baitzen kaleratzera ausartu. Autore batzuen ustetan Lobatxevski eta Bolyairen emaitzak Gauss-engandik zeharka hartutako ideietan oinarritzen dira eta Geometria ez-euklidearraren benetako sortzailetzat Gauss hartu beharko genuke. Beste batzuek, aldiz, ez dute horrelakorik onartzen eta Gauss hasierako pausoetatik aurrera ez zela inoiz joan eta Lobatxevski eta Bolyairi dagokiena aitortu egin behar zaiela esaten dute. Edozelan ere, badirudi Gauss besteen lana kalera aterata poztu egin zela, gero antzeko gai batzuetan Riemann-en ekarpena goraipatu zuenean bezala. Gainera, Lobatxevski Göttingengo Zientzi Elkarteko partaide izendatzea (1842) Gaussen proposamena izan omen zen.

Eredu euklidearrak

Geometria ez-euklidearrak zekarren berrikuntza komunitate matematikoan ez zen berehala nabaritu. Urteak behar izan ziren horretarako eta, batez ere, Eugenio Beltrami (1835-1900) matematikari italiarraren ekarpenak eman zion Geometria horri Matematikan bere tokia. Paraleloen postulatuaren ordez aurkakoa jarrita kontraesanik aurkitu ez izanak, ez zuen segurtatzen ez zegoenik; ondoriozta daitezkeen teorema guztiak idaztea ezinezkoa baita. Baina Beltramik Geometria hiperbolikoaren eskakizunak betetzen dituen eredu bat aurkitu zuen Geometria euklidearraren baitan, eta alderantziz. Honen ondorioz, Geometria euklidearra eta hiperbolikoa, biak, dira posible ala biak ezinezko. Erabat deuseztuta utzi zuen Geometria euklidearra “egia” bakartzat hartzeko joera.

Poincaré-ren eredua. Irudiko lerroak zuzenak dira eta marraztuta dauden triangelu guztiek azalera berdina dute.

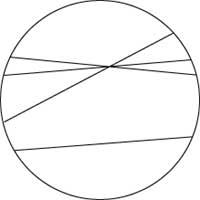
Beltrami-Klein eredua (xehetasunetan sartu gabe) honelako zerbait da: zirkulu baten barruan zuzenak zuzen arruntak dira (zirkuluaren barruan dauden zatiak, noski), baina distantziak neurtzeko modua aldatu egiten da eta angeluak neurtzekoa ere bai. “Luzerak” handiagotu egiten dira zirkuluaren mugara hurbildu ahala eta berez, zirkuluaren korda baten luzera infinitua da. Erraz ikusten da kasu horretan paraleloen postulatu euklidearra ez dela betetzen. Eredu honetan Poincarék aldaketa bat proposatu zuen. Bertan zuzenak, diametroak eta zirkunferentzi zatiak dira (zirkuluaren muga den zirkunferentziarekiko elkartzutak) eta angeluak modu arruntean neurtzen dira, baina ez distantziak.

Esan dezagun, azkenik, Fisika newtondarrak ez bezala, Fisika modernoak espazioa deskribatzeko eredu ez-euklidearrak erabiltzen dituela. Geometria ez-euklidearraren bilakaeraz eta bere eredu euklidearrez interesatuta dagoen irakurleak “Elhuyar” aldizkarian J. Llombart, A. Bernalte eta M. Ensunza-ren artikulu hauek ikus ditzake: Geometria ez-euklidearraren zirriborro historikoa, 11. tomoa, 2. alea (1985), 263-271 orr. eta Plano hiperbolikoaren eredu euklidearak, 12. tomoa, 2. alea (1986), 1-3 orr.