Pitagorasen teoremaren frogapenak

Izen horrekin triangelu zuzenei dagokien emaitza ezagutzen da, hau da, katetuen karratuen batura hipotenusaren karratua da. Pitagoras baino lehen, beste herrialde batzuetan ezagutzen zen; Egipto, Babilonia, Txina, eta abarretan. (Europarrok, beti bezala, geure opilari su).

Badakigu Pitagorasek Egipto eta Babiloniara, eta agian Indiara ere bai, bidaia egin zuela. Bidaia luze haietan ezagumendu erlijioso eta astronomikoez gain ezagumendu matematiko ugari ere bereganatu zuen (Bide batez esan dezagun Pitagoras Buda, Konfuzio eta Lao Tse-ren garaikidea izan zela).

Heleniarrena baino lehenagoko zientzia eta matematika, oro har, erabilgarriak zirela onartu ohi da. Hala ere, zenbait aztarnak matematikaren berezko azterketa egin zela iradokitzen digute. Yale-ko Unibertsitatean dagoen testu kuneiforme batean karratu bat eta bere diagonalak agertzen dira. Alde baten alboan 30 eta diagonal baten alboan 42;25,35 eta 1;24,51,10 zenbakiak ikus daitezke (zenbakiak sistema hirurogeitarrean adierazita daude).

Azken zenbakia diagonalaren eta aldearen luzeren arteko erlazioa da eta ¯2-tik milioirena baino gertuago dago. Doitasun-maila hori Pitagorasen teorema ezagutzeari zor zaio. Pitagorasen teoremaren ezagumendua ez zen triangelu isoszeleetara mugatzen. Esaterako, antzinako problema batean 0;30 luzerako eskailera bat horma baten kontra ipini eta honakoa galdetzen da: hormaren oinarritik zenbat urrunduko da eskaileraren beheko muturra, goiko muturra 0;6 unitate jaisten bada?.

2. irudia. Pitagorasen teoremaren frogapena arabieraz

1350. urte ingurukoa

Beraz, babiloniarrek teorema ezagutzen zuten jadanik. Izena justifikatzeko, Pitagorasen teorema lehenbizi pitagorikoek frogatu zutela esan da, baina hori ezin da egiaztatu; ez baitago frogarik.

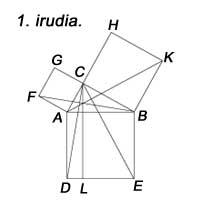
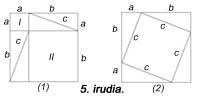
Pitagorasena ez, baina beste frogapen batzuk ezagutzen ditugu. Euklides-en lehenengo liburua 47. eta 48. proposizioekin bukatzen da, zeinetan Pitagorasen teoremaren eta bere alderantzizkoaren frogapenak agertzen baitira. Euklidesek frogapenean proportzioak erabiltzea saihestu egin zuen, elkarneurgaiztasunak sor zitzakeen zailtasunak zirela medio. Euklidesek 1. irudia erabiliz ordea, frogapen dotorea egin zuen. Frogapena honelaxe lortzen da: AC aldearen gainean eraikitzen den karratua FAB triangeluaren bikoitza da edo CAD triangeluaren bikoitza, hots, AL laukizuzenaren berdina. Bestalde, BC aldearen gaineko karratua ABK triangeluaren bikoitza da, edo BCE triangeluaren bikoitza, hau da, BL laukizuzenaren berdina. Ondorioz, karratuen batura laukizuzenen baturaren berdina da, hots, AB karratua.

Euklidesen meritua da Pitagorasen teoremaren ondoren alderantzizko teorema frogatu izana: triangelu batean, alde baten gaineko karratua beste bien gaineko karratuen batura bada, azken bi aldeek osatzen duten angelua zuzena da.

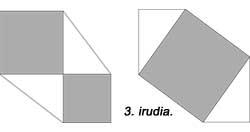
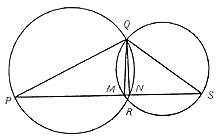
Euklidesena ez da teoremaren frogapen bakarra. 2. irudian 1350. urtean egindako frogapen arabiarra ikus daiteke. Errenazimentuko Leonardo da Vinci zientzigizon ospetsuak ere bere frogapena eskaini zuen (3. irudia). Elisha Scott Loomis-en “The Pythagorean Proposition” liburuan (1940), 367 frogapen azaltzen dira, bakoitzak ikuspegi desberdina erabili duelarik.

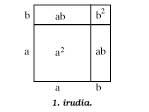
Teoremaren frogapen asko jolas moduan erabiltzen da askotan. Esaterako 4. irudian agertzen den joku klasikoan. 3 eta 4 aldeetako karratuak 5 piezatan bana daitezke eta gero 5 aldekoa osatu.

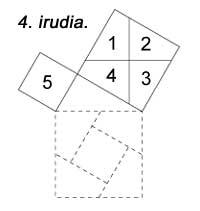
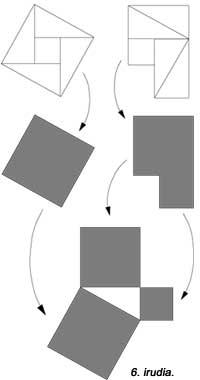
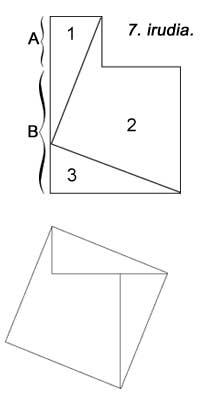
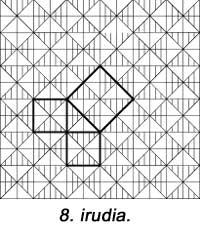
Hurrengo irudian beste bat agertzen zaigu, baina hor ez dira unitate karratuak erabili. 6.a aurrekoaren antzekoa da. Guztietan bost pieza erabiltzen da. Hilario Fernández Long-ek, Buenos Airesko Unibertsitateko Errektore ohiak, hiru piezako puzzlea asmatu zuen teorema frogatzeko (7. irudia). Beste bat agertzen da. Eta azkenean, 8. irudian mosaiko baten laguntzaz frogatzen da, babiloniarrek egiten zuten bezala.

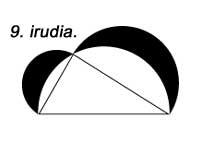
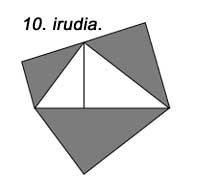
Aldeen gainean karratuak eraiki beharrean zirkuluerdiak eraikiz gero propietate bera betetzen da (9. irudia). Gauza bera gertatzen da antzeko triangeluak eraikitzen baditugu (10. irudia).