The Möbius Ribbon

1989/11/01 Angulo, Patxi Iturria: Elhuyar aldizkaria

• Matematika

We all have in mind the idea that Mathematics is an abstract science. Always immersed in new theories, we do not know how far their hidden arms extend. Apart from that, most of the models used in Mathematics are not seen, perceived, touched, heard and felt in our life as it happens in physics.

Nevertheless, there are contras. We present one of them, the Möbius tape.

Before you read on, grab paper and scissors.

To get the Möbius tape take a long strip of paper, turn to one end (180¼) and then glue the two ends into the ring. The ring you have in your hands does not have two faces or two sides, as you could imagine.

The common rings have two faces, each painted in different colors. Our ring, the Möbius tape, cannot be painted in two colours. If you paint from a point, when you finish you will discover that you have painted the whole tape, since as we said before the tape has only one side (only the one you have painted).

The problem does not end there, but the same thing happens with the edge. From one point, the entire edge runs and returns to the same point. Thus, the Möbius tape has one side and one edge.

This surface is special for another reason. If you take into account at one point the normal vector to the surface, after turning it across the surface and parallel to the edge, the normal vector will be in the opposite direction (that is, if at first it was looking to the left, after turning it will be looking to the right). Therefore, at the same point you would have two normal vectors. This means that the surface is not directional. Of course, all this should be taken into account with respect to a three-dimensional coordinate system.

This film was shot down by mathematician and astronomer August Ferdinand Möbius in 1858. Since then the Möbius tape has become a toy of topologists.

Prepare paper and scissors because we will do manual work.

If you cut a normal tape in half, you'll get two equal tapes. What if you try to do the same with the Möbius tape? (do it) … Of course! two tapes, only one. And the new resulting tape is from Möbius or normal? You confirm … although the new tape is bifacial, it has two spirals, four turns of 180º or two full tours of 360¼. The new tape is narrower (half the other) and at the same time longer (double length). If you cut it back in half, you'll get two tapes (narrower but of equal length) but chained (you can't separate them).

Now we're going to do another job.

Take a strip on paper and divide the two sides into three parts by two horizontal straight lines.

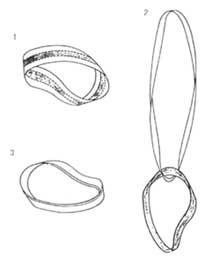
Paint the central parts of another color. Now the Möbius tape is formed. This tape is divided into three parts, being the central of different colors. Cut the tape down these straight lines. Once finished, you will have two tapes, one in the center of the original tape and one on the sides. The painted central is the Möbius tape. The other is a tape with two spirals. Both have the same width, but the second is longer (double). With these two tapes you can form a Möbius tape of triple thickness, surrounding the other (painted) in the greater length. As we have said, this triple tape consists of two other tapes, the other (painted) between the side tapes.

The same effect can be achieved by taking three strips of paper and gluing the six ends two by two after turning to one end (180 ¼) as one.

To get the Möbius tape we have averaged (180 ¼) back to one end of the paper strip. However, this is not the only possibility to get a single face tape. And if we turn to the end with a t’erdi (540¼) or two laps with a t’erdi (900¼), or…, we can get a tape of this type.

Therefore, we can divide the tapes into two classes: one side and two sides. The first will be achieved by giving an extreme an odd number of means; the second, when the number of means is even.

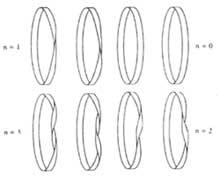
Turns can be left or right. The tapes thus obtained are homeomorphs in topology, equivalent in our language. However, you cannot convert one to another.

So the one-sided ribbons cut through the center will give us a ribbon. The characteristics of the new xingola are as follows: it has half the width of the original and double the length; it is a two-sided tape; if the original tape has half turn n, the new tape will have 2n+2 turns or n+1 spirals (full turn 360¼). Therefore, the Möbius tape (n=1) will give us a tape of four turns or two spirals.

On the contrary, the two-sided tapes give us two equal tapes after half (before we did not want to use this verb). Characteristics of the new tapes: they have the same length as the original and half of their width; they are two-sided tapes; they have as many turns as the original ones; in the case of n=0 the tapes appear loose, in the other cases two chained tapes are obtained.

Numerous attempts have been made to industrially use the Möbius belt, such as the conveyor belt that Lee de Forest invented in 1923 a film with this form, self-cleaning filters, burning belts, conveyor belts for the typewriter, etc.

In the arts we can also see some examples: the M.C you know in this section. Made by artist Escher; Swiss sculptor Max Bill; the two-metre-high ribbon in front of the Washington D.C. Museum of History and Technology revolves around himself.

In a Möbius tape you could write the following incomplete sentence: “On one occasion there was a story that started like this…”

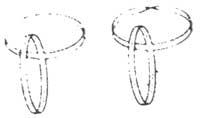
The paper structures represented in Figure 5 are similar, the one on the left consists of two normal rings. The right is a normal ring and a Möbius tape. Trim both dotted lines and compare the results obtained.

So far we talked about the Möbius tape. However, we cannot fail to mention another mathematical model related to the Möbius tape. Möbius tape was obtained using a strip of paper. However, this new model could be achieved by gluing two Möbius tapes with glue. The new model, called the Klein bottle, has been devised by mathematician Felix Klein.

The Klein bottle cannot be built as easily as the Möbius tape. However, assuming that the glass can be reduced and pulled as we want, you can get the bottle as seen in the final image. The resulting bottle has a hole and edge. Theoretically it can be achieved without holes or edges, although in reality (physically) it is not possible. It is a bottle that is characterized by having a single face, the same characteristic as the Möbius tape.

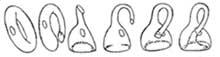
We have assumed that the material to build the Klein bottle, the glass, is very flexible. In Topology, branch of mathematics, such assumptions are legitimate. In fact, topology studies the invariant positional properties to size and shape changes. Perhaps the simplest way to define topological properties is to say that they are geometric properties that remain unchanged to extensions and summaries.