La cinta de Möbius

1989/11/01 Angulo, Patxi Iturria: Elhuyar aldizkaria

• Matematika

Tots tenim al cap la idea que Matemàtiques és una ciència abstracta. Sempre immersos en noves teories, no sabem fins a quin punt els seus braços ocults s'allarguen. A part d'això, la majoria dels models que s'utilitzen en Matemàtiques no es veuen, perceben, toquen, senten i se senten en la nostra vida com ocorre en la física.

Malgrat això, existeixen contres. Et presentem una d'elles, la cinta de Möbius.

Abans de continuar llegint, agafa paper i tisores.

Per a aconseguir la cinta de Möbius agafa una llarga tira de paper, fa mitja volta a un extrem (180¼) i després encola els dos extrems formant l'anell. L'anell que tens a les teves mans no té dues cares o dos costats, com es podia imaginar.

Els anells comuns tenen dues cares, cadascuna d'elles pintada de diferents colors. El nostre anell, la cinta de Möbius, en canvi, no es pot pintar a dos colors. Si et poses a pintar des d'un punt, quan acabis descobriràs que has pintat tota la cinta, ja que com hem dit abans la cinta té una sola cara (només la que has pintat).

El problema no acaba aquí, sinó que passa el mateix amb l'aresta. Des d'un punt, tota l'aresta corre i torna al mateix punt. Així, la cinta de Möbius té un costat i una vora.

Aquesta superfície és especial per un altre motiu. Si es té en compte en un punt el vector normal a la superfície, després de fer-li un volt a través de la superfície i paral·lel a la vora, el vector normal quedarà en sentit contrari (és a dir, si al principi estava mirant cap a l'esquerra, després de donar-li la volta estarà mirant cap a la dreta). Per tant, en un mateix punt tindries dos vectors normals. Això significa que la superfície no és direccional. Per descomptat, tot això ha de tenir-se en compte respecte a un sistema de coordenades tridimensionals.

Aquesta cinta va ser derrocada pel matemàtic i astrònom August Ferdinand Möbius en 1858. A partir de llavors la cinta de Möbius s'ha convertit en una joguina de topólogos.

Prepara el paper i les tisores perquè farem treballs manuals.

Si curtes per la meitat una cinta normal, obtindràs dues cintes iguals. Què passarà si intentes fer el mateix amb la cinta de Möbius? (fes-ho) …Clar! no s'aconsegueixen dues cintes, només una. I la nova cinta resultant és de Möbius o normal? Tu confirma … encara que la nova cinta és bifacial, té dues espirals, quatre girs de 180° o dos gires completes de 360¼. La nova cinta és més estreta (la meitat de l'altre) i alhora més llarga (doble longitud). Si ho talles ara de nou per la meitat, obtindràs dues cintes (més estretes però d'igual longitud) però encadenades (no pots separar-les).

Ara farem un altre treball.

Agafa una tira en paper i divideix les dues cares en tres parts mitjançant dues línies rectes horitzontals.

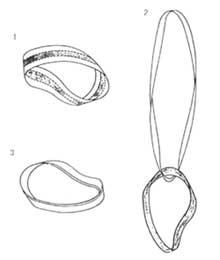
Pinta les parts centrals d'un altre color. Ara es forma la cinta de Möbius. Aquesta cinta està dividida en tres parts, sent la central de diferents colors. Tala la cinta per aquestes línies rectes. Una vegada acabada, disposaràs de dues cintes, una en el centre de la cinta original i una altra en les laterals. La central pintada és la cinta de Möbius. L'altra és una cinta amb dues espirals. Ambdues tenen la mateixa amplària, però la segona és més llarga (doble). Amb aquestes dues cintes es pot formar una cinta de Möbius de triple gruix, envoltant l'altra (pintada) en la major longitud. Com hem dit, aquesta triple cinta està formada per altres dues cintes, l'altra (pintada) entre les cintes laterals.

El mateix efecte es pot aconseguir prenent tres tires de paper i pegant els sis extrems de dos en dos després de donar la volta a un extrem (180 ¼) com una.

Per a aconseguir la cinta de Möbius hem donat la mitjana (180 ¼) volta a un extrem de la tira de paper. No obstant això, no és aquesta l'única possibilitat d'aconseguir una cinta d'un sol rostre. I és que si donem la volta a l'extrem amb una t’erdi (540¼) o dues voltes amb una t’erdi (900¼), o…, podem aconseguir una cinta d'aquest tipus.

Per això, podem dividir les cintes en dues classes: una cara i dues cares. El primer s'aconseguirà donant a un extrem un nombre imparell de mitjanes; el segon, quan el nombre de mitjanes sigui parell.

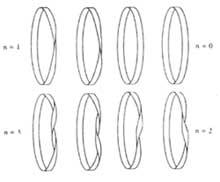
Les voltes es poden donar cap a l'esquerra o cap a la dreta. Les cintes així obtingudes són homeomorfos en la topologia, equivalents en la nostra llengua. No obstant això, no es pot convertir l'una en l'altra.

Així les cintes d'una cara tallades pel centre ens donaran una cinta. Les característiques de la nova xingola són les següents: té la meitat de l'amplària de l'original i el doble de la longitud; és una cinta de dues cares; si la cinta original té mitjana tornada n, la nova cinta tindrà 2n+2 voltes o n+1 espirals (volta completa 360¼). Per tant, la cinta de Möbius (n=1) ens donarà una cinta de quatre voltes o dues espirals.

Per contra, les cintes de dues cares ens donen dues cintes iguals després de la meitat (abans no hem volgut utilitzar aquest verb). Característiques de les noves cintes: tenen la mateixa longitud que l'original i la meitat de la seva amplària; són cintes de dues cares; tenen tantes voltes com les originals; en el cas de n=0 les cintes apareixen soltes, en els altres casos s'aconsegueixen dues cintes encadenades.

S'han realitzat nombrosos intents per a utilitzar industrialment la cinta de Möbius, com la cinta transportadora que Lee de Forest va inventar en 1923 una pel·lícula amb aquesta forma, filtres autonetejadors, cintes calcinantes, cintes transportadores per a la màquina d'escriure, etc.

En arts també podem veure alguns exemples: el M.C que coneixes en aquest apartat. Realitzades per l'artista Escher; l'escultor suís Max Bill; la cinta de dos metres d'altura situada enfront del Museu d'Història i Tecnologia de Washington D. C. gira sobre si mateix.

En una cinta de Möbius es podria escriure la següent frase incompleta: “En una ocasió hi havia un conte que començava així…”

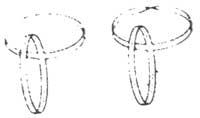
Les estructures de paper representades en la figura 5 són similars, la de l'esquerra està formada per dos anells normals. El de la dreta és un anell normal i una cinta de Möbius. Retalla totes dues línies de punts i compara els resultats obtinguts.

Fins aquí hem parlat de la cinta de Möbius. No obstant això, no podem deixar d'esmentar un altre model matemàtic relacionat amb la cinta de Möbius. La cinta de Möbius s'obtenia utilitzant una tira de paper. No obstant això, aquest nou model podria aconseguir-se pegant dues cintes de Möbius amb cola. El nou model, denominat ampolla de Klein, ha estat ideat pel matemàtic Felix Klein.

L'ampolla de Klein no es pot construir tan fàcilment com la cinta de Möbius. No obstant això, suposant que el cristall es pot reduir i tirar com volem, es pot obtenir l'ampolla tal com es veu en la imatge final. L'ampolla resultant té un forat i una aresta. Teòricament es pot aconseguir sense forats ni arestes, encara que en la realitat (físicament) no és possible. Es tracta d'una ampolla que es caracteritza per tenir una sola cara, la mateixa característica que la cinta de Möbius.

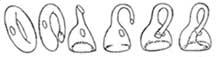
Hem suposat que el material per a construir l'ampolla de Klein, el cristall, és molt flexible. En la Topologia, branca de les matemàtiques, aquest tipus de supòsits són legítims. De fet, la Topologia estudia les propietats posicionals invariants als canvis de grandària i formes. Potser la forma més senzilla de definir les propietats topològiques és a dir que són propietats geomètriques que romanen invariables a les extensions i resums.