Mathématiques face à la 2ème langue

1991/10/01 Ansa, Lurdes - Elhuyar Edizioak Iturria: Elhuyar aldizkaria

• Matematika

Elhuyar: D'où venez-vous à ce sujet?

J. F. L.:

Ce n'était pas un sujet qui avait été soulevée brusquement; avant d'être professeur à l'Université, il a enseigné les mathématiques dans une Ikastola modèle B. Ils étaient des élèves de cycle supérieur et le saut à l'enseignement moyen était immédiat. Bien que ces élèves aient travaillé en mathématiques en espagnol, l'intention des enseignants était d'intégrer le plus grand nombre d'élèves dans le modèle D de l'enseignement moyen, il n'était pas illogique de penser qu'ils pourraient avoir des problèmes. Cette recherche a commencé à croire qu'il était urgent de vérifier, analyser et classer cette prévision.

PaP: Quels sont les objectifs de ce travail?

J. F. L.:

L'un des principaux objectifs que nous avons fixés était d'établir les bases scientifiques pour repenser l'enseignement de sorte que les élèves du modèle B n'aient pas de problèmes pour travailler les mathématiques en basque en rejoignant le modèle D dans l'Enseignement Moyen. Avant, cependant, il fallait analyser s'ils avaient ou non des problèmes, puisqu'il aurait pu être possible qu'il n'y ait aucun problème et que le nôtre fût un simple soupçon.

L'objectif du modèle B est clair : Permettre à tout élève de 8ème cours de suivre n'importe quel sujet en basque et en espagnol, pour lequel chaque centre mettra les moyens nécessaires. Selon cette approche théorique, en passant à l'Enseignement Moyen, ils n'auraient pas d'inconvénient ni en espagnol ni en basque, mais les choses ne se produisent presque jamais ainsi (et je veux dire les mathématiques, qui est notre sujet d'étude), entre autres, parce que dans certains centres, nous travaillons les mathématiques que nous étudions en espagnol.

L'objectif principal de cette thèse serait lié à cette préoccupation: Autrement dit, si l'objectif marqué par le modèle B est atteint ou non, et comment il affecte l'élève en cas de non-respect.

PaP: Pourquoi étudier le binôme mathématique/langage?

J. F. L.:

Bien qu'il semble que les mathématiques et la langue soient espacées, dans tout processus d'enseignement (y compris les mathématiques), l'influence de la langue est indéniable. Comme le dit Sanchez Carrion dans son livre Un avenir pour notre passé, le professeur enseigne tous les sujets, mais travaille toujours la langue. Par conséquent, vouloir analyser les relations entre les mathématiques et la langue n'est pas si étrange.

Dans des contextes bilingues, le problème est aggravé, car pour être vraiment bilingue, il faut être capable d'utiliser les deux langues dans n'importe quel sujet, même en mathématiques. Ici commence à se poser des problèmes réels, car cela n'est pas entièrement conforme au modèle B.

L'utilisation des deux langues, pour sa part, ne devrait en aucun cas empêcher l'assimilation des différentes matières, ce que personne n'admettrait. Dans n'importe quel programme, qu'il soit monolingue ou bilingue, des objectifs minimaux sont fixés, même si chaque centre est libre de choisir la méthodologie, le matériel, les ressources, etc. Si en plus de l'obtenir arrive à maîtriser la 2ème langue ou la 3ème, mieux.

Même si c'était théoriquement le cas, nous pensions qu'il était intéressant de savoir ce qui se passe réellement et nous y sommes mis en marche; analyser si l'enseignement bilingue constitue un obstacle à l'assimilation des contenus mathématiques.

PaP: À quel point le langage peut-il conditionner le processus d'introduction des mathématiques?

J. F. L.:

Comme mentionné ci-dessus, le langage conditionne l'enseignement de toute matière, et les mathématiques ne sont pas en dehors de cette règle générale. Jusqu'à présent, nous avons parlé entièrement des mathématiques, mais, suivant la taxonomie de Bloom, il convient de différencier différents processus tels que le calcul, la compréhension et l'application. Dans chacune de ces langues influe différemment. L'importance du langage symbolique dans le calcul est: 3x4=12 est facilement compréhensible dans n'importe quelle langue, bien sûr, avec un minimum de connaissances mathématiques. Sans trop manquer, on peut penser que ceux du modèle B n'auront pas trop de problèmes dans ce processus, mais dans le développement de la compréhension, c'est-à-dire dans la compréhension des manifestations du professeur ou d'un texte écrit. Dans l'application, c'est-à-dire dans la résolution de problèmes, le langage revêt une importance particulière.

Ces deux derniers processus seront ceux que nous devrons analyser en particulier, car en eux il influe sur tout le langage, et dans notre cas, en parlant de la langue 2, pas de la langue maternelle, il nous semblait qu'il pourrait y avoir des problèmes.

PaP: Quel est actuellement le B.O.P.V. et l'organisation de l'enseignement des mathématiques à l'U.B.I?

J. F. L.:

Dans la Communauté Autonome Basque se distinguent trois modèles linguistiques:

1. Modèle A, spécialement destiné aux enfants erdaldunes. Tout est enseigné en espagnol et entre autres objectifs minimaux serait l’apprentissage de l’euskera; apprendre “euskera” et non “euskera”.
2. Le modèle D, où tout se fait en basque, avec l'espagnol comme matière.
3. Enfin, nous trouvons le modèle B que nous avons étudié, dans lequel le basque et le castillan sont traités théoriquement au moins au même niveau, mais ils travaillent les mathématiques, l'écriture et la lecture en espagnol, tandis que les autres matières sont enseignées en basque. Pourquoi est-ce le cas ? Dans certaines théories et études, il a été démontré que pour qu'il n'y ait pas de retard dans ces questions importantes, il est nécessaire de prendre les bases dans la langue maternelle.

Bien que dans le B.O.U. Ces trois modèles diffèrent, il n'en est pas de même dans l'enseignement moyen, car ici il n'y a que deux modèles, les modèles A et D. En théorie, les élèves du modèle B. Une fois terminée, elles seraient déjà préparées pour le modèle A et le modèle D.

L'élève est-il capable de commencer à travailler les mathématiques en espagnol jusqu'à la 8ème année? Ne pas expliquer le retard sur ceux qui ont appris l'euskera?

PaP: Mais quand cette étape est franchie, que signifie le plus inconvénient : les changements linguistiques ou les difficultés du sujet ?

J. F. L.:

Ils ont tous deux une importance et sont tous deux unis. N'importe qui pourrait penser que ce ne serait qu'une faute d'habitude, un défaut d'habitude qui serait dépassé après quelques mois mal. C'est en partie le cas, mais pas seulement cela.

Dans l'Enseignement Moyen, les concepts et le contenu se compliquent en exigeant un plus grand développement linguistique. Les modèles D ou A peuvent aussi avoir ce problème, mais le décalage que peuvent avoir les autres est plus grave. Nous pensons qu'au moment d'analyser les conclusions, nous allons concrétiser davantage, le changement linguistique devrait être fait avant de passer à la CMP.

PaP: Comment avez-vous posé l'étude empirique?

J. F. L.:

Jusqu'à présent, j'ai essayé de rendre compte de l'approche théorique, mais ce travail n'a pas été une simple théorisation. Lors de la conception du studio, il nous a semblé que nous devions faire quatre groupes différents de 8e cours:

Groupe composé d'un certain nombre d'élèves du modèle A (groupe A) avec des élèves du modèle B, deux groupes (groupe B et groupe B) un autre groupe du modèle D (groupe D)

A et B nous avons passé les tests en espagnol et D et B’ en basque. Puisque notre studio était destiné au modèle B, nous avons eu l'occasion de le comparer à deux groupes en basque et en espagnol: Groupe B avec A et B’ avec D.

Pour compléter l'exposition, nous nous sommes rendus aux écoles publiques et aux ikastolas de la Communauté Autonome Basque dans le but d'obtenir environ 900 élèves. Nous ne sommes pas allés dans les centres privés, entre autres parce qu'en Alava nous ne trouvons pas au moins D.

Les variables considérées seraient, d'une part, la mathématique elle-même comme variable dépendante (en distinguant le calcul à aborder dans les mathématiques, la compréhension d'une explication, la compréhension et l'application du texte écrit) et, d'autre part, le niveau d'euskera que nous avons considéré comme variables indépendantes, le type de centre, le modèle linguistique, le niveau socio-économique, l'âge, le sexe, etc.

PaP: Comment avez-vous mesuré le niveau de mathématiques?

J. F. L.:

Nous avons utilisé trois tests différents pour mesurer les connaissances mathématiques:

1. Test étranger EIA ( International Evaluation Achievement ) des États-Unis. En partant de la version espagnole, avant de passer aux élèves, nous devions traduire, valider et contrôler la fiabilité. Ce fut la première étape. Ce test se compose de 40 éléments qui recueillent le contenu du niveau 8: géométrie, fractions, arithmétique,... Avec ce test, on mesure quatre processus différents : calcul, compréhension, application et analyse (ceux relatifs à l'analyse ne sont que deux éléments et n'ont pas d'influence significative sur la recherche à peine pris en compte).
2. Pour mesurer la compréhension de l'exposition du professeur, un professeur de la RCP, après avoir passé une explication précédemment enregistrée en vidéo, nous leur avons demandé à ce sujet. La durée de la vidéo est d'une heure et demie et, bien sûr, elle a eu deux versions, l'une en basque et l'autre en espagnol.
3. Pour mesurer la compréhension du texte écrit, le sujet de probabilité du livre BBB-1 publié par Elhuyar a été sélectionné. Pas complet, il est trop long. Comme le texte était en basque, il a été traduit en espagnol pour passer aux groupes A et B. Après avoir lu le texte, il fallait répondre à plusieurs questions, les unes en basque et les autres en espagnol.

Tant au moment de choisir le test de probabilité qu’au moment de choisir celui de la vidéo, nous avons limité deux conditions principales: d’une part, le fait que le sujet soit nouveau, puisque si on le traitait précédemment les résultats seraient “non réels”, et d’autre part, le fait qu’il soit un sujet au niveau du développement de l’élève.

Pour mesurer des variables indépendantes, nous avons dû créer quelques tests, mais pas tous, comme le test standardisé D-48 que nous avons utilisé pour mesurer l'intelligence. La preuve que nous avons créé est l'adaptation au conte Peru makur. Dans ce test où après la lecture du conte apparaissent les questions qui lui correspondent, votre niveau de lecture en basque sera mesuré. Trois aspects sont principalement mesurés : vitesse de lecture, pourcentage de compréhension et pourcentage de vitesse de lecture.

Le nouvel outil suppose la réalisation d’un travail “supplémentaire” avant son incorporation à la recherche réelle, comme la réalisation du même test et le contrôle de fiabilité et utilité. Une fois cela fait, je serais prêt à le passer.

PaP: Les outils de mesure utilisés par vous sont-ils utilisables par tout enseignant ?

J. F. L.:

En général oui, bien que certains tests aient été spécialement préparés pour cette recherche (Vidéo test, texte utilisé pour mesurer les probabilités et test basé sur le conte Peru makur). Le reste, cependant, est accessible à toute personne, tant que le niveau des élèves est 8 ou plus (test EIA, test D-48 et conte Peru makur).

PaP: Quelle serait la conclusion la plus remarquable ?

J. F. L.:

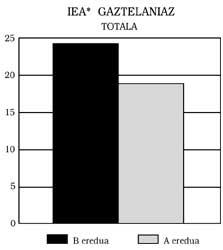
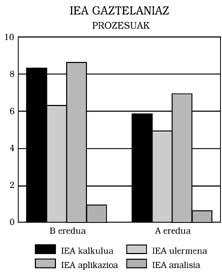
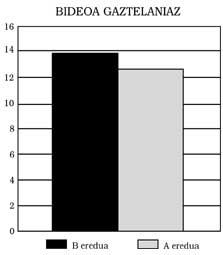
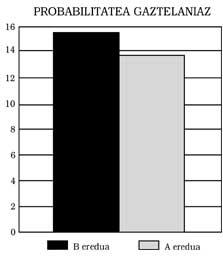
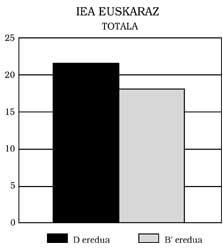
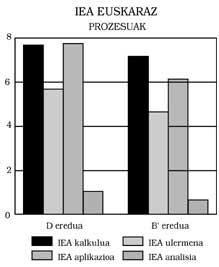
Trois conclusions principales peuvent être tirées : 1) Les élèves du modèle B présentent en répondant en espagnol un niveau minimum équivalent à celui du modèle A. Cela signifie: Ceux du modèle B ne montrent aucun retard mathématique, même si le modèle d'enseignement est bilingue. De plus, comme on peut le voir dans les figures 1, 2, 3 et 4, ils ont obtenu de meilleurs scores que ceux du modèle A. Dans certains cas, en outre, les différences ont été statistiquement significatives, malgré le contrôle de l'intelligence et du niveau socio-économique. N'importe qui pourrait penser que le meilleur score est celui favorisé par l'effet bénéfique du bilinguisme, mais nous n'avons pas osé le dire. Une recherche plus approfondie, qui n'a pas été l'un de nos objectifs.

La raison réelle de cette différence entre les modèles A et B, telle que nous l'avons analysée, serait dans le type de centre. Alors que dans le modèle B se trouvent les ikastolas et les centres publics, dans le modèle A seulement les centres publics (dans les ikastolas il n'y a pas de modèle A). D'autre part, le contexte dans lequel se trouvent les centres publics du modèle A est généralement marginal, dans lequel se présentent d'abondants et fréquents problèmes d'intégration, d'adaptation, etc.

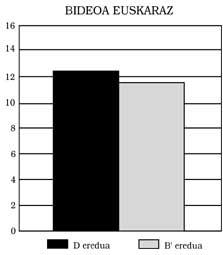
Cela peut être la principale raison de cette différence. 2) En comparant ceux du modèle B’y D, tous les tests ont montré ceux du D au-dessus (voir figures 5, 6, 7 et 8 pour cela). Ces différences sont significatives dans des aspects tels que l'application et l'explication d'un professeur ou la compréhension d'un texte, mais dans d'autres comme le calcul ne se produit pas. Quelle est votre explication ? Ayant un niveau linguistique plus élevé, dans les cas où l'influence de la langue est élevée, ceux du modèle D obtiennent de meilleurs résultats. 3) La troisième conclusion est que les résultats obtenus dans d'autres contextes bilingues ont été contrastés, c'est-à-dire que plus on a travaillé et utilisé la deuxième langue à l'école, plus le degré de compétence est élevé, sans que la première langue ne souffre aucun retard.

Que s'est-il passé dans notre cas? Nous avons observé des différences significatives entre les modèles B. En tout cas, quand on parle du modèle B, il faut dire qu'il s'agit d'un modèle très généralisé, car on peut trouver des modèles B plus euskaldunes et castillanes. Cette classification se fait en fonction de trois variables : pourcentage d'euskaldunes entre professeurs, pourcentage de matières du cycle supérieur qui sont traitées en basque, et enfin, à partir du cours 6, travailler les mathématiques en basque ou en espagnol.

La différence entre les modèles B est réelle, car dans les tests mathématiques le modèle B plus euskaldun obtient un meilleur score. En passant le test en espagnol, il n'y a guère eu de différences. En bref, ce qui est obtenu avec la langue dans certains contextes bilingues, nous l'avons obtenu avec les mathématiques, c'est à dire, plus nous travaillons les mathématiques dans la deuxième langue, plus la compétence est dans la deuxième langue sans retard dans la langue maternelle.

La vérité est que ces résultats n'ont pas fait croire trop d'imprévus en nous, peut-être la plus grande des imprévus a été la différence entre les modèles B et A, que nous attendions des résultats inverses. Nous avons dit, cependant, ce qui peut être votre raison.

PaP: Comment restructureriez-vous l’enseignement devant ces conclusions pour que les résultats soient ‘optimaux’?

J. F. L.:

D'après ce que l'on voit, on modifierait d'abord la structuration des mathématiques dans le modèle B, du moins en ce qui concerne l'utilisation de la langue (si l'on veut atteindre l'objectif principal auquel on a fait référence, qu'une fois le niveau 8 terminé, il soit capable de suivre ses études en basque comme en espagnol). Pour cela, il est nécessaire qu'à partir d'un certain niveau on commence à travailler aussi les mathématiques en basque, et comme nous disons dans les implications pédagogiques de la thèse, dans le système actuel le niveau 6 serait le plus approprié pour faire ce pas.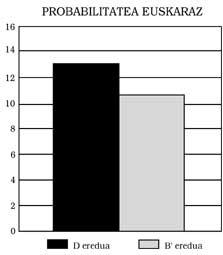

Cependant, avec la prochaine réforme, nous ne savons pas combien ou comment les choses vont changer, même si vous gardez à l'esprit que ce n'est qu'une des voies possibles, qui nous semble plus appropriée, mais chaque centre va marquer son chemin. Pourquoi choisir 6e et pas tout autre? D'une part, parce que le niveau d'euskera des élèves de 6º est assez riche et, d'autre part, parce qu'en distinguant bien l'euskera des limites du castillan, il n'y a pas d'interférences. Comment réaliser cet enseignement? Il n'y a pas de formules magiques, ou bien en donnant quelques thèmes en basque et d'autres en espagnol, ou en traitant chaque sujet en deux langues (introduction et révision dans une langue et le reste), ou de toute autre manière.

Cependant, et dans les implications pédagogiques, nous avons essayé de clarifier, au moment de commencer à travailler les mathématiques dans la deuxième langue, des aspects comme l'élaboration d'un vocabulaire spécialisé, le traitement des problèmes, le développement de la première et de la deuxième langue, etc. Il y a donc quelque chose de élaboré et à quoi arriver si nous voulons devenir vraiment bilingues.