La belleza del caos

1993/12/01 Barragués, J.I. | Alcalde, Cristina Iturria: Elhuyar aldizkaria

• Fisika

Se dice que la ciencia clásica termina cuando se crea el caos. Mientras los científicos trataban de ver un orden (una regla representada por ecuaciones matemáticas de valor universal) mientras estudiaban las leyes de la Naturaleza, el mundo vivía de espaldas a la apariencia desordenada de la realidad.

Las volutas de una onda, los altibajos de la población, los desórdenes atmosféricos (tanto de los acantilados costeros como de las distintas formas que aparecen en la nevera), la acumulación de estrellas en una galaxia y el entramado de vasos sanguíneos son ejemplos de esta parte irregular de la Naturaleza. Esta parte discontinua aparece como una controvertida ante los seres humanos.

Sistemas dinámicos

Durante siglos se han analizado los fenómenos de la Naturaleza desde una perspectiva analítica. El sistema analítico considera detalladamente cada parte de un fenómeno. Sin embargo, esta perspectiva tiene errores para aprender fenómenos muy difíciles. Otra solución es el enfoque sistemático. Según esto, lo mejor es tener una visión general de los fenómenos, aunque se pierdan detalles.

El enfoque sistemático se basa en la noción de sistema dinámico. El sistema dinámico es una colección de objetos que están interrelacionados y evolucionan a lo largo del tiempo según un conjunto de normas.

Los sistemas dinámicos son abundantes en la Naturaleza. Sistema ecológico (donde presas y predadores, hambre, plagas, sequías, ataques humanos, etc.). existen), es un ejemplo de sistemas dinámicos. Las relaciones entre los vecinos determinan si cada especie sobrevive o se pierde.

Los científicos que intentan aprender sistemas dinámicos elaboran copias simplificadas o modelos (corregidas mediante ecuaciones matemáticas) y tratan de hacer funcionar aproximadamente como un sistema real. Introducen el modelo en el ordenador y ven cómo evoluciona a lo largo del tiempo y en qué medida cambia cambiando los parámetros.

Por ejemplo, el sistema ecológico puede incluir climas diferentes, número de habitantes, índice de natalidad, alimentos diarios necesarios, comportamiento animal, etc. El modelo puede acabar con la pérdida de una especie, cuando hay demasiada comida pobre o presa, o cuando hay equilibrio entre especies. Todo depende de la introducción de los parámetros.

En ocasiones, los analistas del sistema analizan el estado final de un sistema e intentan reconstruirlo para investigar las causas que llevaron al sistema a esta situación. Un ejemplo célebre ha sido el siguiente: en la civilización maya VIII. Un modelo para explicar el colapso ocurrido en el siglo XX.

El moderno estudio del caos comenzó en la década de los 60 con un inconveniente descubrimiento: un conjunto de ecuaciones matemáticas de apariencia simple, capaz de describir sistemas dinámicos creados por condiciones de comportamiento rígido e iniciales. Las pequeñas diferencias en la situación inicial generan grandes diferencias en la evolución del sistema. A esto se le ha llamado efecto mariposa. Esta palabra (en medio broma) indica que el movimiento de las alas de una mariposa, realizado aquí y ahora, influye en la climatología de Pekín del mes siguiente.

En la década de los 70, un grupo de científicos trabajó para abrir camino en el reino del desorden. Eran matemáticos, físicos, biólogos, sociólogos, economistas y fisiólogos. Buscaban explicaciones sobre la irregularidad que veían en sus trabajos, utilizando un nuevo sistema de análisis.

Veinte años después, el término caos se ha convertido en una descripción detallada de una tendencia (movimiento científico). Aumento de conferencias, programas de investigación y publicaciones. Botando sobre una mesa salieron unos artículos sobre la extraña dinámica de una pelota, junto con otros sobre mecánica cuántica.

La ciencia del desorden ha creado unas técnicas basadas en el uso de ordenadores. Estas técnicas ofrecen imágenes del caos, estructuras fascinantes, hipnóticas, delicadas y de dificultad infinita.

En realidad, los modelos matemáticos que tratan de mostrar un sistema ecológico, climatológico, económico u otros sistemas de gran dificultad, están formados por miles de ecuaciones y requieren mucho tiempo de procesamiento por ordenador.

Sin embargo, existen algunos modelos que se formulan con pocas relaciones y que tienen una gran dificultad.

Un modelo matemático simple puede partirse de un valor inicial al que _{denominaremos} de principio y, tras unos cálculos, crear un valor final: De acabado. Este último valor se introduce en el modelo como valor inicial y así sucesivamente. La reintroducción de la salida como entrada se denomina realimentación. Hay realimentación, por ejemplo, cuando un micrófono toma la salida del amplificador. Al final, el efecto
es insostenible.

Inicial ₌ 1,1

y calculemos su cuadrado. Se calcula nuevamente _el cuadrado del valor del Xbucal obtenido, etc. La secuencia de números obtenidos será la siguiente: 1,21; 1,4641; 2,14358881;...

Seguid sacando las cuentas. Pero lentamente los números son cada vez más
grandes, sin límites.

Inicial ₌ 0,99

con la siguiente secuencia: 0,9801; 0,96059601; 0,922744694; ... Lentamente, pero esta sucesión se acerca a cero. Sorprende que los números tan próximos entre sí (1,1 y 0,99) tengan un comportamiento tan
diferente.

De acabado _{= (de} inicio)2

Se ha utilizado la norma. También podemos utilizar otras fórmulas que se nos ocurran y ver el comportamiento. Por ejemplo:

De _{acabado =} R.Xinicio (1 _{- De} inicio)

relación, donde R es cualquier número que se elige al principio. Esta fórmula se llama ecuación logística y era una de las primeras que se estudiaban.

En lugar de intentar interpretar la sucesión de números que se obtiene, se puede reproducir gráficamente. En el eje horizontal situaremos los valores de R, por ejemplo entre 2 y 5. En el eje vertical para el punto inicial

(Inicial _{= 0,6,} p. ej.)

Situaremos la sucesión de los valores obtenidos. La figura 1 muestra la representación gráfica del resultado. Aparecen ramas que se separan hasta el infinito.

Atractor de Lorenz

En 1963, Edwarz Lorenz estaba analizando los remolinos que se producen por calentamiento y enfriamiento de las capas atmosféricas. El fenómeno modelizado mediante un sistema de ecuaciones, que parecía sencillo, representó gráficamente el recorrido de la partícula que se deja dentro de un remolino.

La imagen obtenida, hoy clásica, dio a conocer la difícil estructura oculta en las ecuaciones y se convirtió en la bandera de los primeros examinadores del caos. En la figura 2 se muestra la atracción de Lorenz.

Como meteorólogo, Lorenz publicó su descubrimiento en la revista “Journal of the Atmospheric Sciences”, lejos de las manos de físicos, biólogos e ingenieros.

Fractales

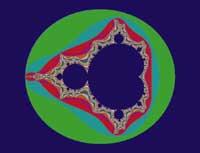
Benoit Mandelbrot, matemático investigador que trabajó en la empresa IBM, inventó un nuevo elemento que más tarde llamó fractal.

Mandelbrot vio una imagen conocida en diferentes lugares: a la altura de los precios de las mercancías, sorprendió a los ingenieros en problemas de ruidos en las líneas telefónicas, etc. En todos ellos se veía la misma característica, una firma que denunciaba el caos. Cuando se analizaban más detalladamente, las reglas de la evolución eran cada vez más difíciles.

Los artistas encuentran la belleza ideal en imágenes clásicas como líneas, planos y esferas, una estructura armoniosa. Sin embargo, la realidad muestra una geometría compleja, rota y mezclada. Descontinuidades, ruidos de repente y comportamientos extraños fueron descritos por Mandelbrot mediante conceptos matemáticos abstractos. El fractal nos da una vía para modelar esta compleja realidad.

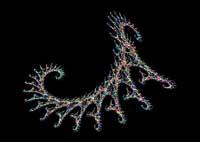
Las curvas fractales pueden generarse por medio de un ordenador y tienen unas formas fascinantes, como se muestra en las Figuras 3-10. Corales, galaxias y dragones fractales representan criaturas tan complejas como las que nos rodean.

La figura 11 muestra una imagen del planeta Acua-Tor. Es un planeta en forma de toroides cuya superficie marina está cubierta por un plasma fractal. Si el lector se fija en él, verá pronto algunas especies que luchan por sobrevivir en Acua-Torre.