Gravidade e peso

1999/09/01 Bandres Unanue, Luis Iturria: Elhuyar aldizkaria

• Fisika

Haika mozo, levántase…

Si dixésemos a calquera persoa "Sentar nesa cadeira e non serás capaz de levantarche sen ningún tipo de atadura", pensaría que estamos moi preocupados. Pero fagamos a proba. Tal e como aparece na imaxe, imos sentarnos, é dicir, co corpo en posición vertical e sen que as pernas entren debaixo da cadeira. Tentemos levantarnos sen cambiar a posición das pernas e mantendo o corpo vertical (sen tiralo cara adiante). Despois de mil intentos e a pesar de utilizar a forza de todos os nosos músculos, non nos levantaremos da cadeira se non colocamos as pernas debaixo da cadeira ou non inclinamos o corpo cara adiante.

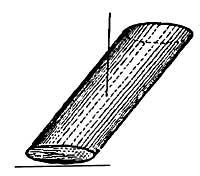
Paira
entender por que sucede todo isto, debemos preocuparnos polo equilibrio de todos os corpos en xeral e da humanidade en particular. Paira evitar que calquera obxecto en posición vertical caia ou se envorque, a vertical que pase polo seu centro de gravidade debe pasar polo interior da base do obxecto. Por iso, o cilindro inclinado que se mostra na imaxe desprenderíase de forma natural. Pero se este cilindro fose máis ancho e a vertical que pasa polo centro de gravidade non saíse polo límite da base, o cilindro non volvería. Por iso, a torre de Pisa, aínda que inclinada, mantense en pé porque a vertical que pasa polo seu centro de gravidade pasa polo interior da súa base (o outro motivo, pero o segundo, é a profundidade das cimentacións enterradas).

A persoa en pé non caerá cando a vertical do seu centro de gravidade pase polo interior da superficie delimitada polos bordos exteriores das plantas. Por iso é tan difícil manterse en pé sobre un só pé e aínda máis difícil manter o equilibrio sobre o arame. Como a base é tan pequena, a vertical do centro de gravidade salgue inmediatamente polo límite da superficie. Déstesvos conta de como andan os mariñeiros vellos? Como toda a súa vida móvese no mar e o chan do barco se balancea, a vertical do seu centro de gravidade sairía facilmente do recinto delimitado polos pés, e para que isto non ocorra, para que esa base sexa o máis grande posible, móvense desa maneira moi peculiar, levando os seus pés moi abertos. Cando están ás costas do barco conseguen así a estabilidade que necesitan mentres o pavimento desprázase, pero cando logo baixan a terra continúan co costume de marear, é dicir, con esa excéntrica marcha.

Tamén se pode pór un exemplo inverso. Ese é o caso de quen teñen una traxectoria elegante polo seu traballo. Hoxe en día non se ve iso entre nós, pero até hai pouco en Euskal Herria, como noutros lugares, paira transportar certas cargas (leite en marmitas, verduras nunha cesta grande, etc.) as mulleres afacían levar a carga sobre a cabeza. Paira poder levar estas cargas sobre a cabeza había que ter a cabeza e o corpo totalmente ergueitos, xa que o menor buzamiento saía da base do corpo a vertical do centro de gravidade (que nestes casos estaba máis arriba do normal) e perderíase o equilibrio de cargas. A través do seu costume, estas mulleres tiñan una marcha esvelta e elegante.

Imos de novo ao compañeiro que deixamos sentado. O centro de gravidade da persoa sentada está situado no interior do seu corpo, xunto á columna e a uns vinte centímetros por encima do embigo. A vertical que pasa por baixo deste punto pasa por detrás das plantas e para que a persoa se levante ten que pasar pola contorna que delimitan as citadas plantas. Por tanto, paira poder levantarse terá que inclinar o corpo cara adiante e así levar adiante o centro de gravidade. Así, cando o punto de apoio estea na vertical do centro de gravidade será capaz de levantarse con forza.

Peso máximo dos corpos

Como
todos sabemos, a Terra exerce una forza tractora sobre os corpos que a rodean, que denominamos "peso". Por outra banda, esta forza é menor a medida que afastamos o corpo da superficie terrestre. Se levásemos un peso dun quilo a unha altura de 6.400 km, é dicir, a unha distancia do centro da Terra do dobre do seu radio, a forza de atracción sería 22, é dicir, catro veces menor, e si medimos o "peso" dese mesmo peso a través do dinamómetro que calibramos na superficie da Terra, en lugar de ter un quilo, teriamos 250 g. Segundo a lei de gravitación universal, a Esfera Terrestre atrae aos corpos que se atopan ao seu ao redor coma se toda a súa masa estivese concentrada no centro, e, por outra banda, esa forza é inversamente proporcional ao cadrado da distancia. Por iso, como a distancia do corpo foi o dobre que a do centro da Terra, a forza de atracción foi 22, é dicir, catro veces menor. Así mesmo, se trasladásemos o corpo a 12.800 km da superficie terrestre, a distancia ao centro da Terra sería tres veces maior e a forza 32, é dicir, nove veces menor. O medidor marcaría agora un "peso" de 111 g. A primeira conclusión é que a medida que nos pesamos a maior altura, máis "lixeiro".

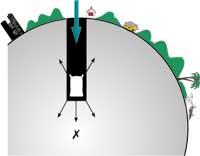
Pero coa mesma lóxica, a lectura que daría o dinamómetro debería ser cada vez maior. Pero iso non é así. Os corpos metidos no interior da Terra son máis pequenos que os "pesos" maiores. Paira entendelo só hai que mirar a imaxe.

Neste caso as fraccións da Terra non están todas ao carón do corpo, como antes (debaixo). Agora uns están debaixo e outros encima, e cada un tira cara ao seu lado. Por tanto, o corpo soportará forzas descendentes e ascendentes. Por último, todas estas forzas únense e, en consecuencia, a forza exercida sobre o corpo é igual á resultante dunha esfera de radio desde a súa posición até o centro da Terra (o que se pode demostrar). Por iso, cando levamos o corpo cara ao interior da Terra, perde "peso". Se o levásemos até o centro da Terra, perdería todo o seu "peso", xa que neste caso todas as partes da Terra que hai ao redor tirarían coa mesma forza en todas as direccións.

Por todo iso, os corpos teñen o seu maior peso na propia superficie da Terra e afastados dela, tanto arriba como abaixo, o "peso"
é menor. Así que se estás un pouco gordo xa sabes que facer: pesa no avión ou no fondo da mina profunda, polo menos ti quedarasche un pouquiño.