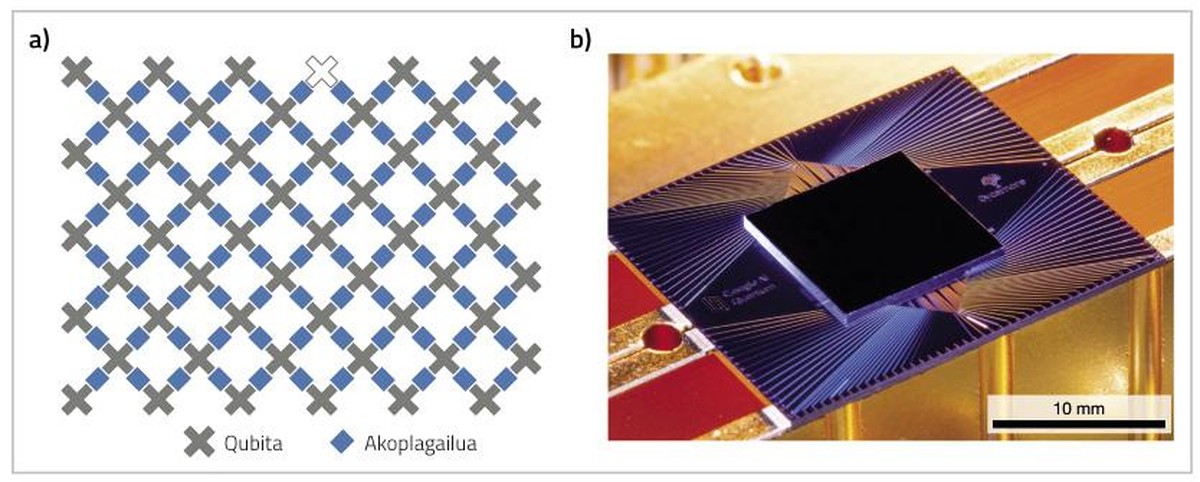
Google and quantum domain
2020/12/01 Arrazola Maiztegi, Iñigo - Kimika Fisikoa Saileko ikertzailea (EHU) Iturria: Elhuyar aldizkaria

The world's fastest supercomputer would take 10,000 years to solve the quantum machine that uses 53 quantum bits (qubit) in 200 seconds[2]. The problem to solve is to predict the answers given by the quantum computer. What do these answers indicate? Nothing concrete. It is a problem designed specifically for the quantum computer to win. While its prediction is done naturally, the normal computer needs resources (classic time and bits) that increase exponentially with the qubit number, which makes it impossible to predict the evolution of many qubits.
The idea of quantum computing is from the 1980s. Then, numerical simulations were becoming more and more important; today, for example, they are essential to predict the spread of virus or make weather predictions. They realized that conventional computers had difficulties to simulate the processes described by quantum physics, and to deal with this problem, another type of computing was proposed: quantum computing.
But, first, what is quantum physics?
Quantum mechanics is a physical theory of more than 100 years old. It describes the interactions among the smallest elements of matter and is at the base of numerous technological discoveries such as laser, magnetic resonance, electron microscope or superconductivity. Quantum physics is a probabilistic theory, so its predictions are probabilistic. Although they are concepts that we now understand and use chance and chance, in their day many physicists did not recognize as basic theory (among them Albert Einstein), because it was unthinkable that the basic processes of nature could be random. Habit has turned the unacceptable and, after years and experiments, almost no one questions the random nature of nature, although it forces us to consider as certain things that seem impossible.
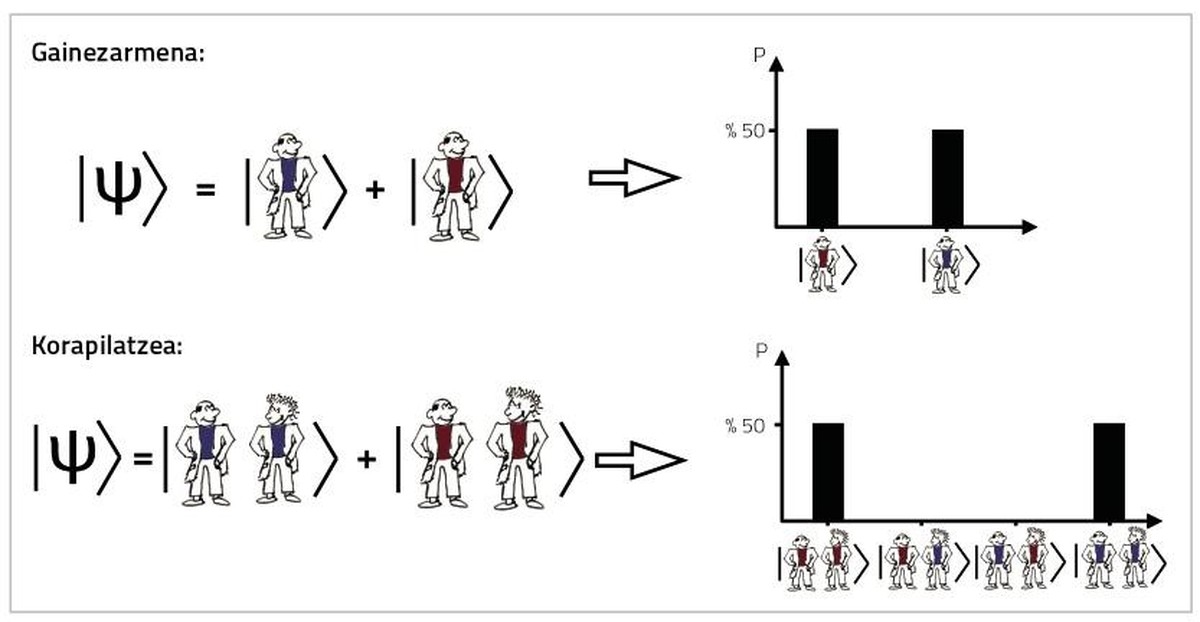
For example, knowing that a friend only has 5 red and 5 blue t-shirts in the wardrobe, seeing him dressed in gabardine from the street, we could think directly that he will have a red t-shirt under 50% chance and a blue with another 50% chance. Although this prediction may be adequate, it is a prediction that comes from our ignorance, since we do not know what shirt the person has dressed that day, but she would know. In the quantum world, however, until our friend removed the gabardina no one would know what color the t-shirt is, neither we nor our friends, no one. It is said that the two possible situations occur “at the same time”. This is what is known as quantum overdisarmament, a phenomenon that we do not experience in the macroscopic world.
In addition, quantum overload knotting allows a special type of correlation between two or more bodies: quantum tangling. Imagine that instead of a friend we have two people and always remember the color of the day's t-shirt, the two equals. Knowing this, we would just have to see a friend's t-shirt to invent the color of the two t-shirts. This is the classic color correlation of the t-shirts of two people. In the quantum world, however, although two friends wear a shirt of the same color with total safety, no one (neither us nor them) would know the color of the T-shirts until one of them opens the gabardine.
What is a quantum computer?
The quantum computer is a computer device that combines these two principles, overdisarmament and tangling. It is very different from the computers we know. Anyone can imitate the work done by the electronic processor of a computer, step by step, using paper and pencil (a billion times slower, yes). Instead, we could never manually imitate the operation of a quantum computer, since it is used of quantum phenomena that do not appear on our scale. Austrian physicist Erwin Schrödinger invented the paradox of Schrödinger's cat by reflecting on the unacceptable situations in which these phenomena appeared in the macroscopic world [3]. According to him, the cat that is inside a box can be alive and dead “at the same time”.
The quantum computer replaces bits by qubits. The bit can be in state 0 or 1, while the qubit can be in both states simultaneously. The two bits have four possible states: 00, 01, 10 or 11. Three bits with 8 different states. Bits 53 9.007.199.254.740.992 (~1016). Possible situations increase exponentially with the number of bits. To perform a certain computation, the normal computer must select one of these different situations. However, the quantum computer can exploit all states at once in a single trial. This is often referred to as “quantum parallelism.”
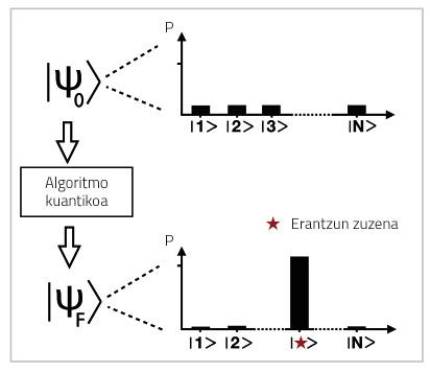
Although it seems the opposite, this does not mean that a 53-qubit quantum computer is by definition 1016 times faster than a 53-bit classic computer. This is largely about measuring/reviewing the problem. The fact of wanting to know the answer to the question posed to the computer forces us to measure it, recovering only one of the possible situations 1016 with a certain probability. What to do to make this situation that the computer gives us the answer we are looking for? The work of quantum algorithms is to take advantage of this parallelism, which is nothing tribal.
There are currently several quantum algorithms [4]. Many, including the one used by Google [1], have an obvious advantage over classic algorithms, that is, they have the ability to solve problems impossible for conventional computers. However, most quantum algorithms are designed to be used in quantum computers of thousands of qubit, something that still does not exist.
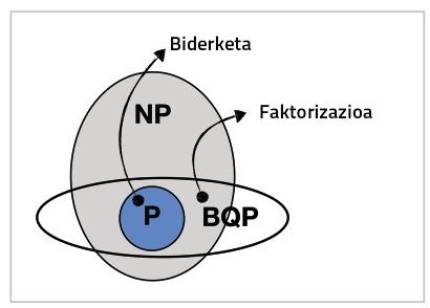
These algorithms solve computer problems. The algorithm that resolves the factorization of integers is the most famous (published in 1994): Shor algorithm. The problem is to give an entire number (e.g. 21), rewrite as a product of prime numbers (e.g. 3×7). The higher the number to be factored, the more difficult it is to find a direct factoring, for example, factoring a 500 digit number can be impossible. This does not happen, for example, with the product: You can also make the calculator that you carry on your mobile the product of two 500 digit numbers. Using the Shon algorithm, a quantum computer could solve this problem for a few seconds.
Why is quantum computing important?
The work of completing this “hierarchy” according to the difficulty of the problem corresponds to the branch of mathematics called theory of complexity. According to this branch, the task of multiplication is found in a group called P and the task of factoring in the group called NP. In summary, the tasks of group P are simple for computers, while those of NP are difficult to solve with the peculiarity that once the answer is known, it is easy to check if the answer is correct (in the case of factoring it is easy to multiply all the factors and compare them with the initial number). This distribution is important, since many mathematicians believe that P is not equivalent to NP, so no one can ever propose an algorithm that makes it a simple factoring problem for computers. You can earn a million dollars in exchange for demonstrating equivalence [5].
What's more, for many experts, this hierarchy of computing problems is universal and sets limits between what nature can combine or not. Algorithms like that of Shon suggest that the computing capacity that allows quantum physics is higher than that which allows classical physics. Therefore, if quantum computing becomes certain, the limit of the problems that nature can combine would be extended, since, in short, nature is quantum. That's why quantum computing is so exciting that it can give us the ability to solve problems we know and don't have.
Although the idea is 40 years old, we are in the childhood of quantum computing. Computers with few built qubit can't implement the Shor algorithm or others. Today many are designing useful quantum algorithms that can implement these small computers. It is possible that the first applications of this type of computers are in the simulation of quantum physics, since with this idea they emerged. Two of the possible applications are the simulation of molecules or superconductors at room temperature for the treatment of diseases [6].
Quantum computers seem to be able to bring computing into a new era. Unfortunately, as often happens in research, today the doubts are more than certainties, around the real capacity of this type of computer. However, in view of the new paradigms of computing that can contribute, it is worth trying to unravel the mysteries of quantum computing.
Bibliography Bibliography Bibliography
Work presented at the CAF-Elhuyar Awards.

Gai honi buruzko eduki gehiago
Elhuyarrek garatutako teknologia





