Google eta nagusitasun kuantikoa

Munduko superordenagailu azkarrenak 10.000 urte beharko lituzke 53 bit kuantiko (qubit) erabiltzen dituen makina kuantikoak 200 segundoan egindakoa ebazteko[2]. Ebatzi beharreko problema zera da: ordenagailu kuantikoak emandako erantzunak iragartzea. Zer adierazten dute erantzun horiek? Ezer konkreturik ez. Espresuki ordenagailu kuantikoak irabaz zezan diseinaturiko problema bat da. Hark iragarpena era naturalean egiten duen bitartean, ordenagailu arruntak qubit kopuruarekin esponentzialki handitzen diren baliabideak behar ditu (denbora eta bit klasikoak), eta horrela ezinezkoa zaio qubit askoren bilakaera aurresatea.

Konputazio kuantikoaren ideia 80ko hamarkadakoa da. Orduan, zenbakizko simulazioak gero eta garrantzitsuago bihurtzen ari ziren; egun, ezinbestekoak dira, adibidez, birusen hedapena aurreikusteko edota eguraldiaren iragarpena egiteko. Ordenagailu arruntek fisika kuantikoak deskribaturiko prozesuak simulatzeko zailtasunak zituztela konturatu ziren, eta arazo horri aurre egiteko, beste konputazio-mota bat proposatu zuten batzuk: konputazio kuantikoa.

Baina, lehenbizi, zer da fisika kuantikoa?

Mekanika kuantikoa 100 urte baino gehiago dituen teoria fisikoa da. Materiaren elementu txikienen arteko elkarrekintzak azaltzen ditu, eta hainbat aurkikuntza teknologikoren oinarrian dago; adibidez, laserra, erresonantzia magnetikoa, mikroskopio elektronikoa edota supereroankortasuna. Fisika kuantikoa teoria probabilistiko bat da, eta, beraz, haren iragarpenak probabilistikoak dira. Gaur egun zoria eta probabilitatea ulertzen eta erabiltzen ditugun kontzeptuak diren arren, bere garaian, fisikari askok ez zuten teoria oinarrizkotzat onartzen (tartean, Albert Einstein), pentsaezina zitzaielako naturaren oinarrizko prozesuak zorizkoak izan zitezkeenik. Onartezina zena onargarria bihurtu du ohiturak, eta, hainbat urte eta esperimenturen ostean, ez du ia inork zalantzan jartzen naturaren zorizko izaera, nahiz eta ezinezkoak diruditen gauzak egiazkotzat jotzera behartzen gaituen.

1. irudia. Sycamore prozesadorea. a) Qubitek elkarri lotuta egon behar dute informazioa prozesatzeko. b) Material supereroalez eginiko prozesadorea da. Iturria: [1].

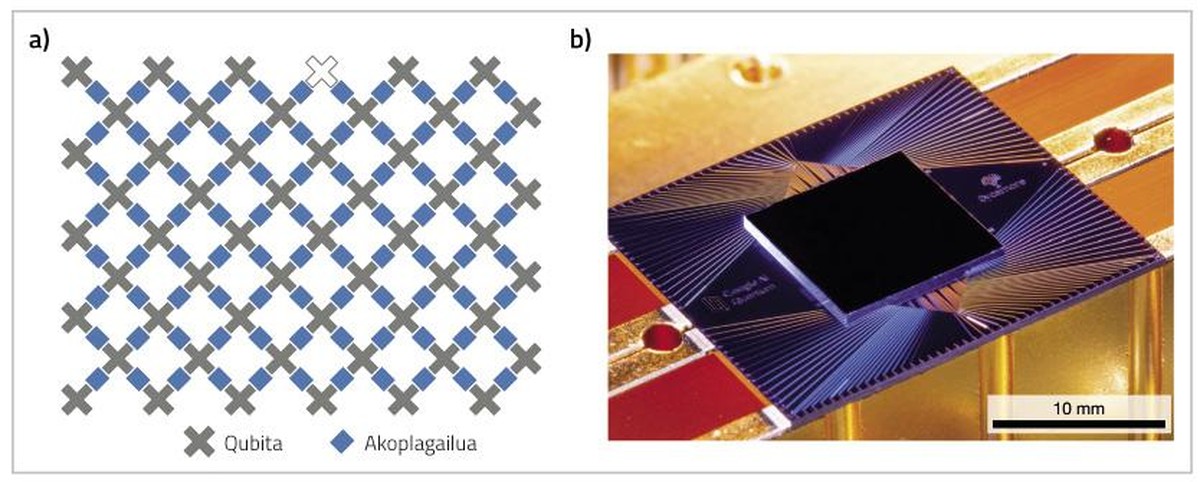
Adibidez, gure lagun batek armairuan 5 kamiseta gorri eta beste 5 urdin soilik dituela jakinik, kaletik gabardina jantzita ikustean, zuzenean pentsa genezake kamiseta gorria izango duela azpian % 50eko probabilitatearekin, eta urdina, beste % 50eko probabilitatearekin. Iragarpen hori egokia izan daitekeen arren, gure ezjakintasunetik datorren iragarpen bat da, ez baitakigu egun horretan zein kamiseta jantzi duen lagunak; berak, aldiz, jakin jakingo luke. Mundu kuantikoan, ordea, gure lagunak gabardina kendu arte inork ez luke jakingo zein koloretakoa den kamiseta, ez guk, ez gure lagunak, inork ez. Bi egoera posibleak “aldi berean” gertatzen direla esaten da. Horri gainezarmen kuantikoa deritzo, eta mundu makroskopikoan esperimentatzen ez dugun fenomeno bat da.

Gainera, bi gorputz edo gehiagoren arteko korrelazio-mota berezi bat ahalbidetzen du gainezarmen kuantikoak: korapilatze kuantikoa. Demagun lagun bat beharrean bi lagun ditugula, eta elkarrekin adosten dutela beti eguneko kamisetaren kolorea, biek berdina. Hori jakinik, nahikoa litzaiguke lagun baten kamiseta ikustea, bi kamiseten kolorea asmatzeko. Bi lagunen kamiseten koloreen korrelazio klasikoa litzateke hori. Mundu kuantikoan, aldiz, bi lagunek kolore bereko kamiseta eraman arren ziurtasun osoz, ez luke inork jakingo (ez guk, ez haiek) kamiseten kolorea zein den, lagunetako batek gabardina ireki arte.

Zer da ordenagailu kuantiko bat?

Ordenagailu kuantikoa bi printzipio horiek, gainezarmena eta korapilatzea, uztartzen dituen konputazio-gailua da. Ezagutzen ditugun ordenagailuekin alderatuta oso desberdina da. Edonork imita dezake ordenagailu bateko prozesadore elektronikoak egiten duen lana, pausoz pauso eta papera eta arkatza erabiliz (mila milioi aldiz motelago, hori bai). Aldiz, sekula ezingo genuke ordenagailu kuantiko baten funtzionamendua eskuz imitatu, gure eskalan agertzen ez diren fenomeno kuantikoez baliatzen delako. Fenomeno horiek mundu makroskopikoan agertuko balira gertatuko liratekeen egoera onartezinez hausnartzean, Erwin Schrödinger fisikari austriarrak Schrödingerren katuaren paradoxa asmatu zuen [3]. Haren arabera, kaxa baten barruan aurkitzen den katua bizirik eta hilik egon daiteke “aldi berean”.

Ordenagailu kuantikoak qubitak erabiltzen ditu biten ordez. Bita 0 edo 1 egoeretan egon daiteke, qubita, aldiz, bietan aldi berean. Bi bitek lau egoera posible dituzte: 00, 01, 10 edo 11. Hiru bitek, 8 egoera ezberdin. 53 bitek, 9.007.199.254.740.992 (~10¹⁶). Egoera posibleak esponentzialki handitzen dira bit-kopuruarekin. Konputazio jakin bat egiteko, ordenagailu arruntak egoera ezberdin horietatik bakarra hautatu behar du. Ordenagailu kuantikoak, aldiz, egoera guztiak esplora ditzake aldi berean, saiakera bakar batean. Horri askotan “paralelismo kuantiko” deritzo.

2. irudia. Gainezarmena eta korapilatzea propietate kuantikoak dira. Objektu kuantikoak bi egoera desberdinetan egon daitezke aldi berean. Irudia: Iñigo Arrazola.

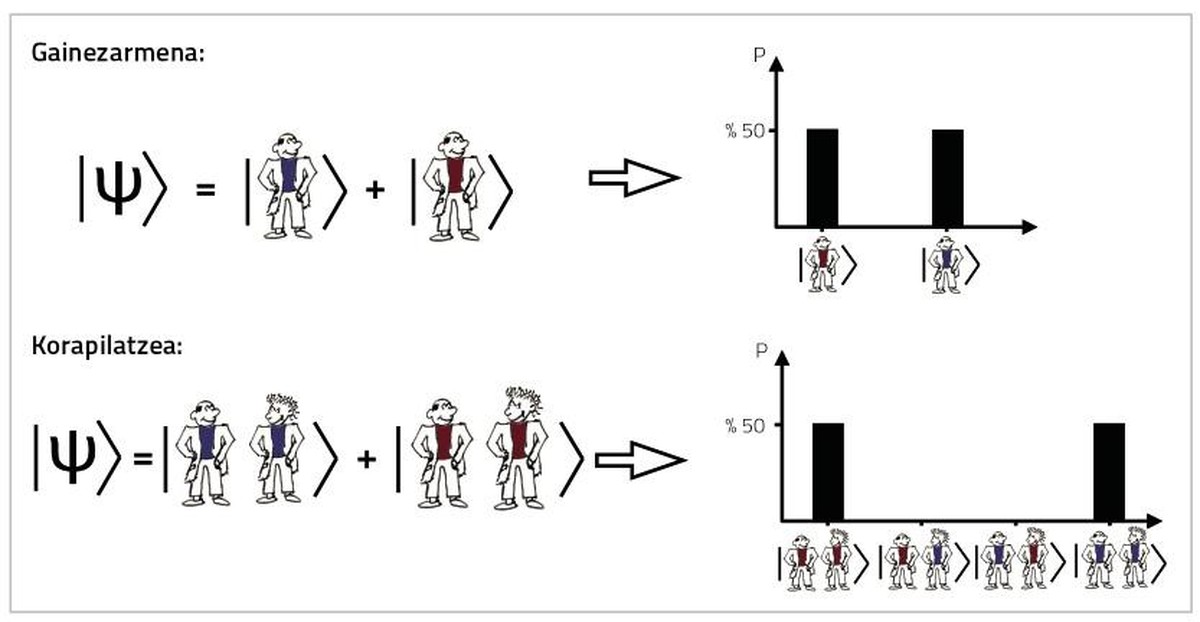
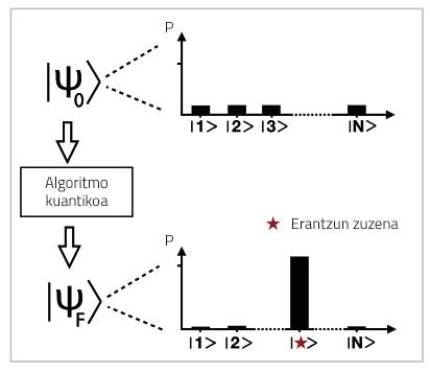
Kontrakoa badirudi ere, horrek ez du esan nahi 53 qubiteko ordenagailu kuantiko bat definizioz 53 biteko ordenagailu klasiko bat baino 10¹⁶ aldiz azkarragoa denik. Neurri handi batean, arazoa neurtzean/begiratzean datza. Ordenagailuari emaniko galderaren erantzuna jakin nahi izateak neurtzera behartzen gaitu, eta 10¹⁶ egoera posibletatik bakarra berreskuratzen dugu, probabilitate jakin batekin. Zer egin ordenagailuak ematen digun egoera hau bilatzen dugun erantzuna izan dadin? Aipaturiko paralelismo hori aprobetxatzea da algoritmo kuantikoen lana, eta hori ez da batere tribiala.

Egun, hainbat algoritmo kuantiko existitzen dira [4]. Askok, Googlek erabilitakoa barne [1], algoritmo klasikoekiko abantaila nabaria dute, alegia, ordenagailu arruntentzako ezinezkoak diren problemak ebazteko gaitasuna dute. Algoritmo kuantiko gehienak, ordea, milaka qubiteko ordenagailu kuantikoetan erabiltzeko diseinatuak daude, eta ez da horrelakorik existitzen oraindik.

Algoritmo horiek konputazio-problemak ebazten dituzte. Zenbaki osoen faktorizazioa ebazten duen algoritmoa da famatuena (1994an argitaratua): Shor-en algoritmoa. Problema honako hau da: zenbaki oso bat emanik (adib. 21), zenbaki lehenen biderkadura gisa berridaztea (adib. 3×7). Faktorizatu beharreko zenbakia zenbat eta altuagoa izan, orduan eta zailagoa da faktorizazio zuzena aurkitzea; esate baterako, 500 digituko zenbaki bat faktorizatzea ezinezkoa bilaka daiteke. Ez da hori gertatzen, adibidez, biderkadurarekin: 500 digituko bi zenbakiren arteko biderkadura mugikorrean daramazun kalkulagailuak ere egin dezake. Shor-en algoritmoa erabiliz, ordenagailu kuantiko batek segundo batzuetan ebatzi ahal izango luke problema hori.

3. irudia. Algoritmo kuantikoak jakin behar du hasierako egoera posible guztietatik ( _0) zuzena aukeratzen ( _F). Irudia: Iñigo Arrazola.

Zergatik da garrantzitsua konputazio kuantikoa?

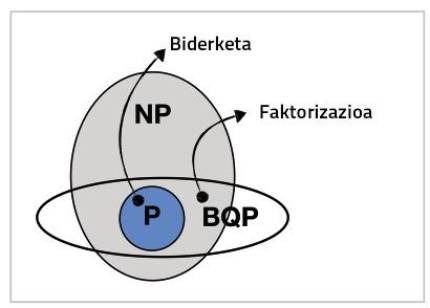
Problemaren zailtasunaren araberako “hierarkia” hori osatzearen lana konplexutasunaren teoria deritzon matematikaren adarrari dagokio. Adar horren arabera, biderketaren ataza P izeneko talde batean aurkitzen da, eta faktorizazioren ataza NP izeneko taldean. Laburrean, P taldeko atazak errazak dira ordenagailuentzat; NPkoak, aldiz, ebazten zailak dira, berezitasun batekin: behin erantzuna jakinda, erraza da erantzuna zuzena den edo ez egiaztatzea (faktorizazioaren kasuan, erraza da faktore guztiak biderkatu eta hasierako zenbakiarekin konparatzea). Banaketa hori garrantzitsua da, matematikari askok uste baitute P ez dela NPren baliokidea, eta, beraz, ezingo duela inork inoiz algoritmo bat proposatu, zeinak faktorizazio-problema erraza bilakatuko duen ordenagailuentzat. Baliokidetasuna frogatzearen truke milioi bat dolar irabazi ditzakezu [5].

Are gehiago, aditu askoren ustez, konputazio-problemen hierarkia hori unibertsala da, eta muga ezartzen du naturak konputa dezakeenaren edo ezin konputa dezakeenaren artean. Shor-ena bezalako algoritmoek zera iradokitzen dute: fisika kuantikoak ahalbidetzen duen konputazio-gaitasuna altuagoa dela fisika klasikoak ahalbidetzen duena baino. Beraz, konputazio kuantikoa egia bilakatuz gero, naturak konputa ditzakeen problemen muga zabalduko litzateke, natura kuantikoa baita, finean. Horregatik da konputazio kuantikoa horren zirraragarria, ezagutzen ditugun eta ez ditugun hainbat problema ebazteko ahalmena eman diezagukeelako.

Ideiak 40 urte dituen arren, konputazio kuantikoaren haurtzaroan gaude. Eraiki dituzten qubit gutxiko ordenagailuek ezin dituzte Shor-en algoritmoa edo bestelakoak inplementatu. Egun, ordenagailu txiki hauek inplementa ditzaketen algoritmo kuantiko erabilgarriak diseinatzen dihardute askok. Posible da halako ordenagailuen lehen aplikazioak fisika kuantikoaren simulazioan egotea, ideia horrekin sortu baitziren. Gaixotasunak tratatzeko molekulen edo giro-tenperaturako supereroaleen simulazioa dira aplikazio posibleetako bi [6].

4. irudia. Konputazio kuantikoak ordenagailu arruntentzat zailak diren problemak ebazteko gaitasuna dauka. Irudian, BQP ordenagailu kuantikoentzat errazak diren problemen multzoa ikus daiteke. Irudia: Iñigo Arrazola.

Badirudi ordenagailu kuantikoek gaitasuna dutela konputazioa aro berri batera eramateko. Tamalez, ikerkuntzan maiz gertatzen den bezala, egun ziurtasunak baino gehiago dira zalantzak, halako ordenagailuen benetako ahalmenaren inguruan. Hala ere, eta ekar ditzakeen konputazio-paradigma berriak ikusita, merezi du konputazio kuantikoaren inguruko misterioak argitzen saiatzea.

Bibliografia

CAF-Elhuyar sarietara aurkeztutako lana.