Engranajeen magia zenbakitan

Engranajeak ardatzen artean higidura transmititzeko erabiltzen diren makina‑elementuak dira. Gurpil horzdunak hamaika aplikaziotan aurki ditzakegu, bai gizakiok sorturiko tramankulu zaharrenetan eta bai naturaren eboluzioak eragindako mekanismo biologikoetan ere [1]. Horretaz gain, gizakion eboluzioan ere, engranajeak nonahi topa ditzakegu; antzinako Greziako Antiziterako mekanismoa da ezagutzen den engranaje bidezko lehenbiziko mekanismoetako bat, planeten higidurei jarraitzeko eraikia [2], [3]; antzinako errota, arma edota era askotako erlojuetan ere asko erabiltzen dira; lehenengo ordenagailuen aitzindariak ere engranaje eta espekaz eginiko gailu mekanikoak ziren, Charles Babbage matematikari ingelesak 1840. urtean asmatua horren erakusle [4] —mendebetez aurrea hartu zien ordenagailu elektronikoari eta Turing-en makinari— . Gaur egun, ezingo genuke engranajerik gabe bizi, egunero erabiltzen ditugun gailu eta makina gehienek engranajeren bat baitute, garraiobide guztietatik etxeko tresna txikietaraino.

Hori nahikoa ez eta, engranajeak teknologia adierazteko nazioarteko ikur gisa erabili ohi dira, baita gailu elektronikoetan ezarpenak adierazteko ikur gisa ere. Baina zergatik? Artikulu honetan engranajeek zenbakien multzoekin (\(\mathbb{N}\subset\mathbb{Z}\subset\mathbb{Q}\subset\mathbb{R}\subset\mathbb{C}\)) duten paralelotasuna aztertuko da, haiek gizakiongan duten magiaren eta erakargarritasunaren adibide gisa.

Hortz-kopurua, zenbaki arruntak (\(\mathbb{N}\)) ala osoak (\(\mathbb{Z}\))?

Engranajeetan, zenbaki-teoriaren historian gertatzen den modura, hortz kopurua kontatzetik hasiko gara. Begi-bistakoa da engranajeek hortz-kopuru osoak izan behar dituztela, hau da, ezinezkoa da, adibidez, hogei hortz eta erdi izatea; hogei edo hogeita bat hortzen artean aukeratu beharko genuke diseinatzaile gisa. Engranajeen hortzak adierazteko, \(z\) aldagaia erabili ohi dugu, ziur aski alemanierazko hortz hitza zahn delako (Ameriketako Estatu Batuetan N erabiltzen dute). Beraz, \(z \in \mathbb{Z}\) edo soilik \(z \in \mathbb{N}\)? Hasiera batean, zenbakien teorian gertatzen den bezalaxe, badirudi soilik zenbaki arrunta izan behar duela hortz-kopuruak, hots, hortz negatiborik ezin dugula eduki. Fisikoki horrela bada ere, eta ez dauka zentzurik hortz negatibo edo zorretan dauden hortzak edukitzea, hortzak barruraka dituzten gurpiletan, hala nola engranaje epizikloidaletako koroetan, hortz kopuru negatiboa erabili ohi da kalkuluetarako. Beraz, \(z \in \mathbb{Z}\) dela esan dezakegu.

Eta... \(\textstyle{z = 0}\)? Engranajeak hortzik ez duela esan nahiko luke; beraz, ez daukagula engranajerik. Ildo horretatik tiraka, galdera oso interesgarri batekin topo egiten dugu: ba ote dago hortz-kopuru minimorik engranajeetan? Praktikan, bi arrazoik mugatzen dute hortz-kopuru minimoa: batetik, higidurak jarraitutasuna izango badu, hortz-kopuru minimo bat beharko dugu; bestetik, erremintak interferentziarik eragin gabe hortz-kopuru minimo bat fabrikatu ahal izango dugu, daukan presio-angeluaren arabera (\(\alpha_n\)): 

\(z_{\min}> \frac{2}{\sin^2\alpha_n}\)

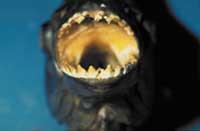
Beraz, engranajeak egiteko oso erabilia den \(α_n = 20°\) duen erremintarekin, 18 hortz (\(z_{\min} > 17,1\)) litzateke interferentziarik eta zuzenketarik gabe fabrikatu daitekeen minimoa (irakurle, konta ezazu, adibidez, goiko irudian ageri den mikroengranajearen hortz‑kopurua... kasualitatea?)

Engranajeen arrazionaltasuna (\(\mathbb{Q}\))

Engranajeen hortzen arteko erlazioak, \(\frac{z_2}{z_1}\), engranajeek lotzen dituzten bi ardatzen arteko abiadura-erlazioa zehazten du. Hots, hortzen arrazoiak zenbaki arrazionalen multzoa osatzen du. Propietate garrantzitsu horren potentziala erakuste aldera, eta engranajeekin lotuta, Huygensen planetarioaren istorioa datorkit burura. Christiaan Huygens XVII. mendeko astronomo, fisikari eta matematikari holandar bat izan zen. Luis XIV. erregeak planetario bat eraikitzeko mandatua egin zion. Huygens ez zen lehenengo pertsona izan planetario bat egiten (Arkimedesen garaitik daude), baina, dakigula, bera izan zen lehena zatiki jarraituak erabiltzen planeten orbiten arteko erlazioa zehazteko. Planeten orbiten periodoa Keplerren datuetatik hartu zuen eta Lurrarekiko zuten periodoa kalkulatu zuen. Horrela, Merkuriok (eguzki-sistemako orbitarik laburrena duen planetak) Lurraren urteko \(\frac{25335}{105190}\) behar du Eguzkiarekiko errotazio bat egiteko [5]. Beraz, hortz-kopuru horiek dituen engranajeekin lotuz gero Lurraren eta Merkurioren arteko mekanismoa, bi planeten orbiten higidurak erlazio zehatz hori beteko luke. Zoritxarrez, begi-bistakoa da ez dela posible horrenbeste hortz dituzten engranajeak erabiltzea planetarioa eraikitzeko; beraz, erlazio horren ahalik eta hurbilena lortzea izan zen Huygensen helburua. Horretarako, zatiki jarraituak erabili zituen; kasu honetan, zatiki jarraitua finitua da (zenbaki arrazionala den heinean). Erraz kalkula daiteke zatiki jarraitu hori, txikitan eskola garaian ikasitako zatikiaren hondarra zatitzaile bezala erabiliz, hots, Euklidesen algoritmoa erabiliz:

\(\frac{25335}{105190}=\frac{1}{4 +\frac{1}{6+\frac{1}{1+\frac{1}{1+\frac{1}{2+\frac{1}{1+\frac{1}{1+\frac{1}{1+\frac{1}{1+\frac{1}{7+\frac{1}{1+\frac{1}{2}}}}}}}}}}}}\)

eta hauek dira hamabi konbergenteak:

\(\begin{matrix} 0 & 1 & 2& 3& 4& 5& 6& 7& 8& 9& 10& 11& 12\\ 0 & \frac{1}{4}& \frac{6}{25}& \frac{7}{29}& \frac{13}{54}& \frac{33}{137}& \frac{46}{191}& \frac{79}{328}& \frac{125}{519}& \frac{204}{847}& \frac{1553}{6448}& \frac{1757}{7295}& \frac{25335}{105190} \end{matrix}\)

Huygensek bosgarren konbergentea aukeratu zuen hurbilketa praktiko eta eraikigarri gisa, \(\frac{33}{137}\) (\(z_1=33\) eta \(z_2 = 137\)), eta egindako errorea \(2,6 ·10^{–6}\) zen. Modu berean egin zuen gainontzeko planeten orbitekin ere (Artizarra, Marte, Jupiter eta Saturno, garai hartan oraindik ez baitziren Urano eta Neptuno planetak ezagutzen). Planetarioa eraikitzen zebilen bitartean, errorea txikitzeko beste modu bat aurkitu zuen: bi etapatan eginez transmisioa, lau engranaje erabiliz, 9. konbergentea erabili ahal izan zuen:

\(\frac{204}{847}=\frac{12}{7}\cdot\frac{17}{121}\)

Modu horretan, errorea \(1,7·10^{–7}\)-ra txikitzea lortu zuen.

Zenbaki lehenak (\(\mathbb{P}\))

Behin transmisio-erlazioaren arrazionaltasuna ikusita, zenbakien teoriarekin jarraituz, zenbaki lehenak azaltzen zaizkigu. Zer gertatzen da bi engranajeren hortzen zatitzaile komunetako handiena 1 denean? Hortz-kopuruak zenbaki lehenak badira, baldintza hori beteko da; horregatik, engranajeen diseinuan oso onartua dago zenbaki lehenez (edo gutxienez elkarrekiko lehenez, koprimoak) osatuta dauden hortz-kopuruak erabiltzea engranajearentzat: zkh (\(z_1\), \(z_2\)) = 1. Adibidez, 16 eta 27 hortz dituen engranaje batek ere beteko luke lege hori; nahiz eta zenbakiok lehenak ez izan, elkarrekiko lehenak dira 24 eta 33.

Bi arrazoi nagusi daude erabilera hori justifikatzen dutenak. Alde batetik, hori gertatzen denean pinoiko hortz bakoitzak ez du koroako hortz berdina joko behin eta berriz, baizik eta hortz guztietan joko du birak eman ahala; horrela, higadura hortz guztien artean banatuko da. Zenbaki lehenak erabiltzeko beste arrazoi bat makinetan gerta daitezkeen dardaren akoplamendua ekiditea da. Makinen osagai bakoitzak frekuentzia natural bat du, eta balio horretan edo haren multiploetan (harmonikoetan) dardara izan dezake. Hortaz, hortz-kopuru lehenez osaturiko engranajeek transmisio-erlazio ez osoa emango dute eta dardara horiek gutxituko dituzte.

Baina izan al daiteke engranaje bat irrazionala? Hau da, izan al dezake transmisio‑erlazio irrazionala? Praktikan zentzurik ez daukan arren, adibidez, bitxikeria gisa ageri dira urrezko proportzioa (proportzio aureoa) duten engranajeak [6], hortz‑kopuru ez osoz eginikoak:

\(φ=\frac{1+\sqrt5}{2}=\frac{1}{1+\frac{1}{1+…}}\approx\frac{10,4721361…}{6,4721361…}≈1,61803398874989484820…\)

Engranajeen irrazionaltasuna (\(\mathbb{I}\))

Honezkero, argi geratu da zenbaki arrazionalez beteta dagoela engranajeen mundua eta hortzen erlazioak matematikariek historian zehar landu izan dituzten hainbat bitxikeriarekin erlazioa dutela. Baina, ba al dago zenbaki irrazionalik engranajeen munduan? Bai, noski, nola ez. Bi engranajek higidura transmititu ahal izateko, haien hortzen artean dagoen pauso diametralak berdina izan behar du. Hau da, pinoiko hortz batek koroan egindako sartu-irtenak arku berdinean eragin behar du eta, jakina den moduan, zirkunferentziaren diametroaren eta perimetroaren arteko erlazioa zenbaki irrazional batek zehazten du. Dena den, ingeniariok, praktikoak (eta hein handi batean arrazional) garen aldetik, modulu izeneko aldagaiaren barruan ezkutatu dugu \(\pi\). Hala, modulua hortzen arteko pauso diametrala eta \(\pi\)-ren arteko erlazioa da (\(m=\frac{p}{\pi}\)), normalizatuta dago eta hortzaren tamainarekin erlazioa du. Oso praktikoa da engranajeen kalkuluetarako; adibidez, jatorrizko diametroa \(d_p = m·z\) denez (jatorrizko zirkunferentzian hortz beste pauso daudenez: \(\pi⋅d_p = p·z\)), engranajeen ardatzen arteko distantzia erraz kalkula dezakegu modulua eta hortz-kopurua jakinik: \(a=\frac{d_{p1}}{2}+\frac{d_{p2}}{2}=\frac{m}{2}(z_1+z_2)\). Hortzaren gainontzeko neurriak ere moduluarekiko normalizatuta daude (adibidez, erreferentziazko erremintaren A profilak, addendum-ak eta dedendum-ak, \(1·m\) eta \(1,25·m\) neurria dute hurrenez hurren). Beraz, esan dezakegu engranajeak irrazionalak ere badirela hein handi batean.

Mundu konplexua (\(\mathbb{C}\))

Horrenbestez, zenbaki errealen multzoari (\(\mathbb{R}\)) dagozkion propietate eta misterioak engranajeen bidez errepasatu ditugu. Eta zenbaki konplexuak?

Zenbaki konplexuak zati erreal eta zati irudikariz osatutako zenbakiak dira, eta, oro har, honela idatz daitezke \(z\) plano konplexuan: \(z = x + iy\), non \(i\) unitate irudikaria erabiltzen den zenbaki konplexua lortzeko. Leonhard Euler matematikari handiak ezarri zuen \(i\)-ren erabilera, \(\sqrt{-1}\) adierazteko eta \(x^2 + 1 = 0\) moduko ekuazioen emaitza gisa. Puntu honetan, Euler ardatz hartuta, bilkaria edo inboluta kurba ageri zaigu, engranajeetan gehien erabiltzen den profila hain zuzen. Inboluta kurba lau bat da, eboluta izeneko beste kurba lau baten gainean irristatu gabe errodatzen duen zuzen baten puntu batek sortzen duena [7]. Eulerrek proposatu zuen lehenengoz 1765 urtean profil hori engranajeen hortzentzat, ordura arte profil zikloidalak erabiltzen baitziren, erlojugintzan besteak beste. Gaur egunean, profil bilkariak dira engranajeetan erabilienak, bi ezaugarri garrantzitsugatik: fabrikatzeko erraztasunagatik eta abiadura angeluarra konstante mantentzen delako engranatze-prozesu osoan zehar (praktikan, hortzak ez direnez guztiz zurrunak, transmisio-errore txiki bat izaten dute).

Baina, engranajeetan non erabiltzen dira zenbaki irudikariak? Orain arte, hortz zuzenak ikusi ditugu; hau da, hortzaren zabalerako edozein planotan berdinak dira. Baina hortz inklinatuak edo helikoidalak dituzten engranajeak oso erabiliak dira. Kasu horietan, zabaleran \(β\) angelua biratuz doa profila, eta plano irudikaria daukagu (zenbaki konplexuetan bezala). Horrela, orain arte ikusitako aldagaiak orokortu ditzakegu: hortz birtualak (\(z'=\frac{z}{\cos^3β}\)), itxurazko modulua (\(m_t =\frac{m}{\cosβ}\)) … eta gisa horretako kontzeptuak azaltzen zaizkigu engranajeen munduan ere.

Horrenbestez, engranajeen bidez errepasatu ahal izan ditugu zenbakien multzoak.

ERREFERENTZIAK

[1] I. Leturia, “Engranajeak erabiltzen ditu intsektu batek jauzi egiteko”, Elhuyar, 301, (2013)

[2] Wikipedia, "Antiziterako mekanismoa"

[3] BBC, The 2,000-Year-Old Computer

[4] Wikipedia, "Analytical Engine"

[5] C. Huygens, Opuscula postuma, (1703)

[6] OscarPuzzle, Irrational Gears (Youtube) (2015)

[7] Wikipedia, "Bilkari (geometria)"