Edith Clarke: a woman's heritage in science
2021/05/09 Markel Fernandez Zubizarreta - APERT ikerketa-taldea. Bilboko Ingeniaritza Eskola (EHU) | Iker Aretxabaleta Astoreka - APERT ikerketa-taldea. Bilboko Ingeniaritza Eskola (EHU) | Endika Robles Perez - APERT ikerketa-taldea. Bilboko Ingeniaritza Eskola (EHU) | Iñigo Kortabarria Iparragirre - APERT ikerketa-taldea. Bilboko Ingeniaritza Eskola (EHU) | Unai Ugalde Olea - APERT ikerketa-taldea. Bilboko Ingeniaritza Eskola (EHU) Iturria: Elhuyar aldizkaria

Although few know, Edith Clark, the first US engineering, invented the transformed Clark, so used in the study of three-phase networks and electric machines to simplify calculations. This transformation meant the simplification of the calculations necessary for the study of three-phase systems of electrical networks, and later of electric machines.
Initial years
Edith Clarke was born in 1883 in the American County of Howard (Maryland). After studying Mathematics and Astronomy he spent his first years in teaching. Later, although he began his civil engineering studies at the University of Wisconsin, he left George A to work at the American Telephone and Telegraph. Assistant engineer Campbell. At that time, when there were no computers, those few women dedicated to science worked as "human computers". That is, his main obligation was to perform complex and long calculations. However, Edith Clark broke the boundaries of that time as part of the project to build the first transcontinental telephone line from New York to California. His experience in working in electrical circuits and transmission lines and his passion for his work in general led him to conduct electrical engineering studies. She studied at the Massachusetts Institute of Technology (MIT), being the first woman to receive this degree at MIT.
However, with this degree from MIT it also did not achieve the same professional status as men engineers. In fact, in 1920 he entered General Electric (GE), where he led a group of "female computers" that calculated the mechanical stresses of turbines and rotors. Finally, in 1923, after two years as a professor at the University of Istanbul, she returned to GE and became the first electrical engineer in the United States. In turn, he joined the American Institute of Electrical Engineers, breaking the other two female borders of the time. On the one hand, she was the first woman to publish a scientific article (Steady-state stability in transmission systems-calculation by means of equivalent or circle diagrams) and, on the other, the first woman with full voting rights.
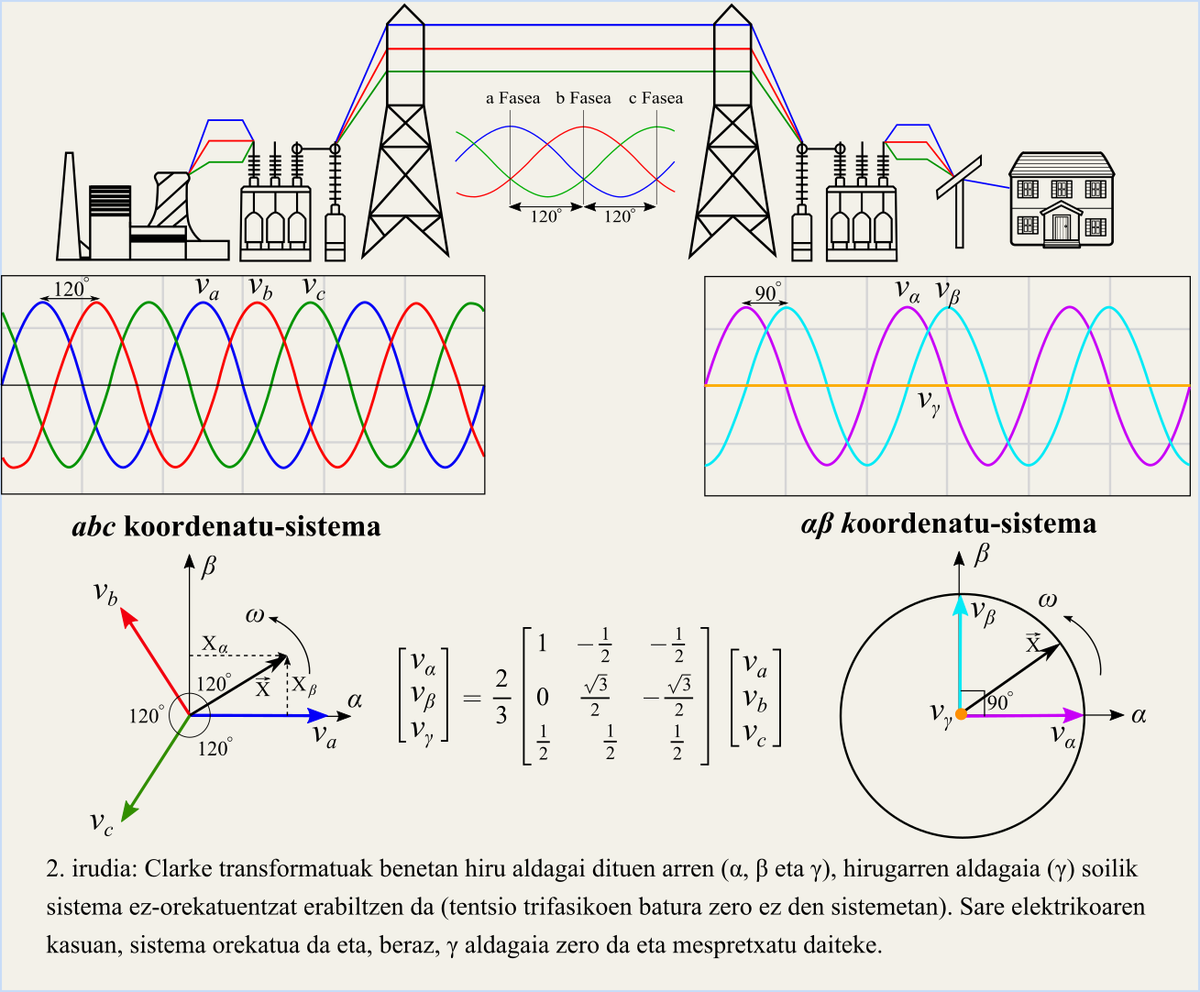
Edith Clarke worked at GE until 1945 and between 1947 and 1956 taught at the University of Texas until his retirement. Throughout his professional career, he got various things in the field of electricity and transmission lines. Among others, he proposed equivalent circuits that can be used to study the stability of power systems and published a study on transmission lines over 300 miles in length. In addition, years later, in 1943, he published the book Circuit analysis of A-C power systems and published several scientific articles with researcher Charles Concordia, among others. The transformation that bears his name derives from his work with Charles Concordia: Clarke transformed. This mathematical transformation consists in transforming three-phase electrical systems into a system of two independent dimensions, facilitating the complexity of calculations. Currently, in addition to transmission lines, there are other applications in which this transformation matrix is widely used (Figure 2).
Transformed Clarke and Power Grid
The current electrical network is three-phase, that is, it consists of three sinusoidal signals with a phase of . XX. At the beginning of the 20th century, the calculation of long transmission lines of the power grid was very complex due, among other reasons, to the need to perform all calculations manually. The transformation matrix proposed by Edith Clark significantly simplified the analysis of these systems. In fact, the three-phase system (coordinates a, b, c) with a gap between itself, converts to stable two-dimensional systems (coordinates <unk>, b) with a gap of . This system resulting from the transformation is represented by the fasor describing the radius circle of the mains voltage (Figure 2), whose rotation speed is equal to the frequency of the electrical grid (Figure\ 2).
Despite the above, it should be noted that the two-dimensional system obtained after the transformation retains all the information that the three-phase system contained, that is, the variables <unk> and b store all the information of the variables a, b and c. But how is it possible? This is explained by taking into account an indispensable condition that the electric grids meet: the three-phase system must necessarily be balanced. A balanced system means that the instantaneous sum of the three tensions is zero. Thus, by representing variables a, b and c as vectors (Figure 2), their sum is zero. This condition ensures that two system variables are known and the third. On the other hand, this transformation has another interesting feature. Indeed, the gap between <unk> and b is not random, as this gap ensures that both variables are independent from each other. Thus, changes made to a will not be reflected in < and vice versa.
Clarke transformed into current applications
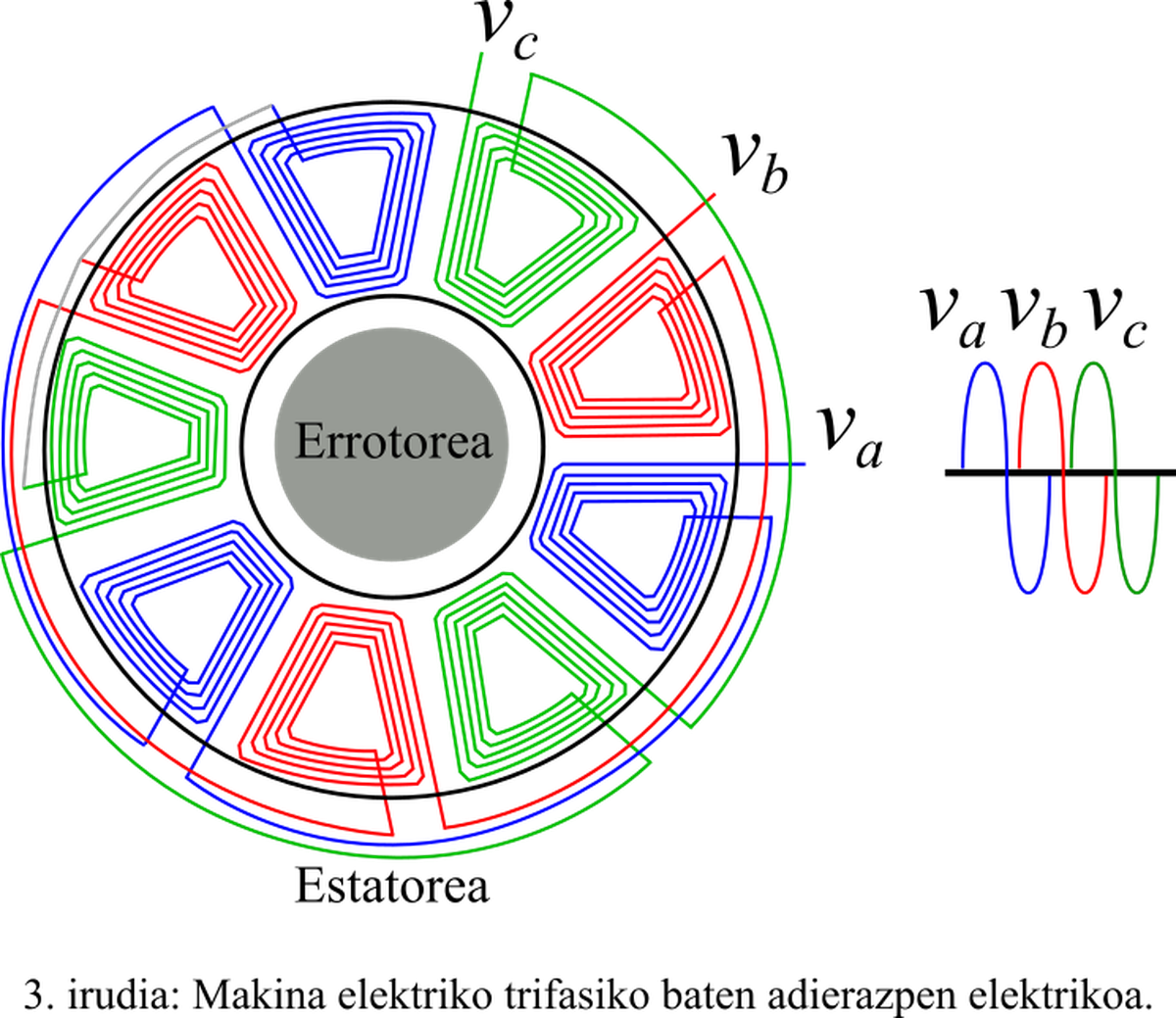
Although the three-phase network is a good example of application in which transformed Clarke is used, its applications go further. Among others, we can highlight the control used in electric machines. Electric machines can consist of three or more phases. However, the simplest system is the three-phase one, which will be taken as a model. However, instead of having three transmission lines, the electric machine consists of three coils with dephase, connected to the same point (Figure 3). In addition, the transformer can be used with the voltage, current and flow of the machines.
As mentioned, this transformation provides two independent variables. This is very important in the control of electric machines, as it allows distributed control of the magnetic flow and the moment of the machine. By adding a small explanation, the first of these variables represents the current of the stator (part that does not turn in machine) of the electric machine generating the magnetic flow. The other variable indicates the current of the rotor (part rotating in the machine). The latter is the current that generates force to spin the axis of the electric machine. In short, these transformations aim to convert the behavior of an AC electric machine into the behavior of a much simpler DC electric machine. In short, Clarke's transformation transforms three coupled variables into two independent variables needed to control the electric machine. In this way, the control of three-phase machines can be carried out similarly to DC machines, significantly decreasing their complexity.
Finally, the boom experienced in the last decade by high-power electric machines has made polyphatic machines (more than 3 phases) have been used in more and more applications. Although the transformed clarke was designed for use in three-phase systems, with a small transformation it can be easily adapted to polyphatic machines. Thus, thanks to the work of this woman many engineers, physicists, mathematicians and researchers can solve complex calculations in their day to day by transforming Clarke.
References
[1] James E. Brittain (1985). From Computer to Electrical Engineer: The Remarkable Career of Edith Clarke. IEEE Transaction on Education, vol. E-28, pp. 184-189.
[2] Tony Furfari. Women in Electrical Engineering.
[3] R. Clarke (1926). Steady-state stability in transmission systems calculation by means of equivalent circuits or circle diagrams. Journal of the A.I.E.E., vol. 45, pp. 365-373.
[4] Edith Clarke Biography: Biography Books (2019).

Gai honi buruzko eduki gehiago
Elhuyarrek garatutako teknologia