El desordre i la mort de la humanitat: són sinònims?
2021/07/14 Ainhoa Oliden Sánchez - Kimika Fisika saileko doktoregaia (EHU) | Rebeca Sola Llano - Kimika Fisika saileko irakaslea (EHU) Iturria: Elhuyar aldizkaria
Representar l'estat. Quatre persones en una habitació quadrada: dues columnes i dues files, una a la mateixa distància. Des de la perspectiva superior diríem que aquesta ordenació és simètrica, és a dir, ordenada (figura 1).
Canviem l'escenari. S'ha demanat a totes les persones que es troben dins de la sala que facin un pas que s'ha limitat a quatre adreces: cap endavant, cap endarrere, cap a l'esquerra o cap a la dreta. Podria ser, sense acord entre ells, que tots avancessin. Si això fos així, es mantindrà l'ordre. La probabilitat que cadascuna d'aquestes persones prengui aquesta decisió és reduïda, d'un quart perquè cadascuna pot moure's en quatre direccions. Doncs la probabilitat que quatre persones actuïn per igual és encara menor, 1 part 4x4x4x4 o 1 part 256.

Si en lloc d'avançar cap endavant, cap endarrere, cap a l'esquerra o cap a la dreta simultàniament, la distribució no sofriria canvis, però la probabilitat de mantenir l'harmonia continuaria sent de 4 a 256 o d'1 a 64. Lleuger ascens, gairebé menyspreable [1].
Anem a l'últim escenari. En aquesta ocasió se'ls ha donat la llibertat d'anar a qualsevol direcció sense limitacions de mobilitat. Aquí sí. A causa de les situacions possibles i interminables, serà suficient fer un pas per a trencar definitivament l'ordenació simètrica i augmentar el desordre en un instant.
Tot això, definint una situació senzilla de quatre persones. Trobar milions i milions d'àtoms que poden moure's en la naturalesa en infinites direccions ens porta a concloure que els processos que es produeixen de manera espontània tendeixen a augmentar el desordre. Un clar exemple d'això és l'enfonsament d'un vaixell, l'explosió d'un volcà, el flux d'aigua descendent dels rierols de les muntanyes… El científic Rudolf Clausius va arribar a la mateixa conclusió en 1850, i per primera vegada va definir el terme entropia i va establir el segon principi de la termodinàmica, amb la finalitat de donar una explicació als processos que ocorren en la naturalesa [2].
Què és l'entropia?
El primer principi de la termodinàmica és ben conegut. Potser no explícitament, però tots hem sentit parlar del principi de conservació de l'energia equivalent. “L'energia no es produeix ni es destrueix, sinó que es transforma” [3]. En grec, la paraula termodinàmica significa moviment de calor, i el científic Rudolf va veure que, en sistemes de diferent energia, aquest moviment sempre es produïa amb la tendència a igualar l'energia [4].
Vegem més clarament amb un simple exemple: un got ple de gel (Figura 2). Què passarà amb els glaçons? Amb el temps el gel es fon i desapareix. Per què? Per les diferents concentracions d'energia que podem trobar en el sistema. Inicialment, les temperatures o energies del gel i el mitjà són diferents. Per tant, aquest flux d'energia es transmet de major a menor concentració i aquestes energies tendiran a igualar-se, és a dir, el mig aporta calor al gel i la temperatura del gel puja i es fon mentre el mig baixa.
Clausius va definir l'entropia (S) per a indicar si aquest moviment o distribució d'energia era uniforme o no, i va establir el segon principi de la termodinàmica: com més uniforme es dispersi aquesta energia, major entropia [4]. Dit d'una altra manera, quan l'energia es distribueix de forma totalment uniforme, l'entropia del sistema és màxima [5]. Per tant, l'entropia d'un cos homogeni es distribueix i expandeix automàticament en tot el seu volum, passant d'un estat ordenat a un estat desordenat [6].
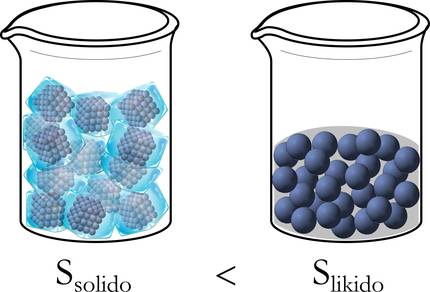
Per a comprendre millor, reprenguem l'exemple de gel abans esmentat. De fet, al principi, en estat sòlid, les molècules estan ben ordenades: empaquetades, sense llibertat de moviment. En canvi, en passar a estat líquid tenen un marge de desplaçament més ampli i es desordenen, i més encara quan es transforma de líquid a gas (figura 3).
Revisem ara la teoria de Rudolf en el dia a dia. Per exemple, és més possible trobar la nostra habitació potes enlaire que trobar tot ordenat i correctament. Podem pensar que el millor lloc per a guardar els nostres pantalons és l'armari, amb cadascun d'aquests vestits penjats en el seu propi penjador. No obstant això, pot ser cedida en el sòl, sobre la cadira, en el llit o en qualsevol altre lloc. Sembla que està escrit! Aquesta realitat és incontrolable i inevitable, ja que la probabilitat de mantenir l'ordre es considera menyspreable. Per tant, buscar la causa de l'augment de l'entropia seria insignificant.
Com aconseguir ordre?
Hem après amb experiència que és molt difícil aconseguir els nostres desitjos sense esforç. Al seu torn, el segon principi de la termodinàmica sosté que els processos no propis només poden produir-se treballant en el propi sistema.
Fins ara, no obstant això, hem parlat únicament de processos propis (processos espontanis). Els fets considerats no espontanis són aquells que no es produeixen de manera natural. I a què diem natural? Procés de creixement continu de l'entropia. Estem acostumats a veure processos que suposen un augment de l'entropia i, sense adonar-nos, els considerem normals.
Per tant, tot procés de la nostra vida és senyal que el temps avança. Si de sobte observéssim que l'entropia disminueix, l'única manera d'explicar-ho seria pensar que el temps va cap endarrere. Suposem que estem veient una pel·lícula a l'inrevés i veiem un plat caigut de la taula al sòl, a l'inrevés. Segurament riuríem, perquè sabem que el fet que ocorri d'aquesta manera és impossible [1].
Per tant, és clar que per a successos no espontanis és necessari aplicar un treball extern [6]. No obstant això, malgrat la disminució de l'entropia, l'entropia total del sistema i del seu entorn augmentarà al llarg del temps, pel fet que l'ordenació d'un sistema implica sempre la desordenación d'uns altres.
Anem cap a la mort tèrmica?
Es pot dir que l'entropia de l'univers va creixent contínuament [7], donant així una visió pessimista per al futur. Un continu augment del desordre significa que les diferències de concentració d'energia estan desapareixent. En igualar totalment les energies dels sistemes, no es podran aconseguir o fer més treballs ni es podran produir més canvis. En conseqüència, podríem dir que ens estem acostant a la mort tèrmica?
Pensem en un mòbil. Els telèfons mòbils funcionen gràcies a les bateries, és a dir, a la reacció química que es produeix en el seu interior. Generen un flux d'energia des del punt de major a menor concentració, la qual cosa provoca el funcionament del mòbil. Quan s'esgota la reacció química dins de la bateria o s'aconsegueix l'estat d'equilibri, on no podrem veure canvis nets, el gradient desapareix i s'obté un nivell d'energia uniforme. En altres paraules, el mòbil mor.
Per a ressuscitar el telèfon es necessita energia humana i prové fonamentalment del sol. La nostra estrella està composta majoritàriament per hidrogen, que, com tota la resta, s'està degradant. Donada l'elevada densitat i temperatura, es produeixen reaccions termonuclears en les quals els nuclis dels àtoms d'hidrogen es converteixen en nuclis dels àtoms d'heli [4, 8]. De nou, un exemple d'igualació de les concentracions d'energia. Com sabem avui dia, al final de l'hidrogen solar, l'energia s'igualarà totalment, i el mateix ocorrerà amb qualsevol altra estrella de l'univers, així com amb tot el que hi ha en l'univers.
Si el segon principi de la termodinàmica és aplicable a tot l'univers, les concentracions d'energia en tots els llocs s'estan igualant i el cosmos s'està degradant. Quan aquesta energia està totalment escalonada, l'entropia aconseguirà el seu màxim i a partir d'aquí no ocorrerà res. Encara que l'energia continuarà present, no hi haurà tendència al canvi ni a generar fluxos d'energia per a iniciar reaccions.
Hauríem de perdre l'esperança?
De fet, si ens fixem en la creació de l'univers, podem veure un príncep de llum. Vam néixer del no-res, i no serà possible tornar a crear-ho de zero! Com indica l'equació matemàtica, 0 = (+1) + (-1). És possible que d'on no hi ha res es pugui generar energia positiva i negativa per a després generar una mica major a través dels canvis [1].
En qualsevol cas, no és tan greu. El procés trigarà diversos anys a arribar al final i l'univers, tal com existeix, no sols viurà en el nostre temps, sinó en tota la vida de la humanitat i de la Terra [9].
Bibliografia:
[1] I. Asimov. 1977. Cent Preguntes Bàsiques sobre la Ciència. Alianza Editorial, Madrid.
[2] R. Clausius. 1864. Abhandlungen über die mechanische Wärmetheorie. F. Vieweg, Harvard College Library.
[3] P. Atkins, J. Estafa. 2010 Atkins' Physical Chemistry. Oxford University Press, la Xina.
[4] http://www1.euskadi.net/harluxet/
[5] R. Clausius. 1875. The mechanical theory of heat. Macmillan, Londres.
[6] R. J. Silbey, R. A. Alberty. 2001. Physical Chemistry. John Wiley & Sons, Inc.
[7] https://zthiztegia.elhuyar.eus/terminoa/eu/entropia.
[8] H. En Karttun, P. Kröger, H. Oja, M. Poutanen, and K. J. Donner. 2016 Fonamental astronomy. Springer, Finland.
[9] Ian Ridpath. 2016 Oxford Dictionary of Astronomy. Oxford University Press.

Gai honi buruzko eduki gehiago
Elhuyarrek garatutako teknologia