Trous noirs: un peu d'histoire (I)

1993/02/01 Arregi Bengoa, Jesus Iturria: Elhuyar aldizkaria

• Astrofisika

Ces dernières années, les trous noirs sont devenus des objets de grand prestige. Ces astres, qui ont une intensité suffisante pour que la zone de gravité ne sorte pas de son influence même la lumière elle-même, permettent à rien d'autre de sortir de son intérieur. Par conséquent, les trous noirs sont des zones d'espace totalement isolées du reste de l'univers. Ils continueront à ingérer la matière qui pourrait être dans leur environnement, mais en ne pouvant rien retirer de leur intérieur, en aucun cas vous pouvez obtenir des informations de celui-ci ou de savoir ce qui se passe là. Ces particularités étonnantes sont devenues quelque chose d'attrayant et ont transpercé le domaine de la science, apparaissant souvent aussi dans les domaines cinématographique et littéraire.

Figure .

Si le nom de «trou noir» a été proposé il ya vingt ans et la théorie moderne des trous noirs n'a pas beaucoup d'années de plus, l'idée des astres massifs qui ne laisseraient pas échapper la lumière est beaucoup plus ancienne. J. 1783 Mitchel, professeur à Cambridge, a publié un travail calculant le rayon nécessaire pour que la vitesse d'échappement d'une étoile de la même densité que le soleil soit celle de la lumière. Comme on le sait, la vitesse d'échappement est la vitesse nécessaire pour qu'un corps sorte de la gravité d'un autre. Imaginons que nous voulons envoyer un espace à une autre planète.

Si la vitesse de l'espace est inférieure à la vitesse d'échappement de la Terre (11,2 km/s), l'espace s'élèvera ou perdra de l'énergie (vitesse) et à un moment donné sa vitesse sera zéro. Puis le mouvement se détourne et retombe sur Terre. Si la vitesse dépasse 11,2 km/s, l'énergie de l'espace sera suffisante pour avancer dans l'espace interplanétaire et échapper à l'influence de la Terre.

Comme nous l'avons dit précédemment, si la vitesse d'échappement d'un astre était supérieure à celle de la lumière (300.000 km/s), la lumière elle-même ne pourrait pas sortir de son champ de gravité. La vitesse d'échappement solaire est de 618 km/s. J. Selon les calculs de Mitchel, une étoile de densité du Soleil devrait avoir un rayon cinq cents fois plus grand que celui du Soleil pour que la lumière soit également limitée à son champ de gravité.

Le scientifique britannique n'était pas le seul à avoir remarqué et traité ce problème. P. S. Laplace, dans un travail publié en 1799, a montré que la vitesse d'échappement d'une étoile de radio R = 1,48.10-27 M (avec la masse de l'étoile M en kg) était la vitesse de la lumière. Ces objets que nous avons décrits, Laplace les a appelés « corps sombres ».

Il semble logique de penser que ces idées étaient basées sur la théorie corpus de la lumière. Au siècle suivant, cependant, la théorie des ondes a été imposée et de ce point de vue, il était plus difficile de comprendre comment la gravité pouvait affecter la lumière. C'est peut-être pourquoi Laplace n'a pas inclus les conjectures au sujet des corps obscurs dans des publications ultérieures.

Les références à des corps sombres ou des trous noirs n'étaient pas XX. Réexposer jusqu'au début du XXe siècle. Le développement d'une théorie complète et complète ne pouvait être fait que lorsque Einstein a publié en 1915 la théorie de la relativité générale et les astrophysiques ont commencé à comprendre les dernières étapes de l'évolution des étoiles. On peut penser que compte tenu de la duplicité onde/fraction sur laquelle se base la mécanique quantique, considérant que la lumière est formée de photons, les travaux de Mitchel et de Laplace pourraient redevenir utiles.

Figure .

Cependant, ces travaux ont été réalisés du point de vue de la mécanique classique et ne tiennent pas compte de certaines particularités de la lumière. Nous ne pouvons pas comparer la lumière générée par une étoile à l'espace. Cette dernière perd de la vitesse en augmentant la hauteur, mais la vitesse de la lumière est constante et ne diminue pas malgré s'éloigner de l'étoile. Un des résultats de la théorie d'Einstein est comment la gravité affecte la lumière.

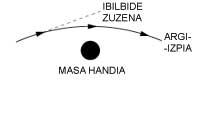
Selon la théorie générale de la relativité, le parcours de la lumière est le chemin et la distance la plus courte entre deux points. Quand l'espace est vide, cette voie est directe, mais quand il y a un corps, son champ de gravité déforme l'espace environnant, inclinant aussi le chemin de la lumière. La première figure montre un exemple de cet effet : le rayon de lumière qui traverse l'espace devient quand il passe par un corps massif.

C. 1916 Schwarzschild a utilisé la théorie d'Einstein pour analyser la situation de l'espace autour d'un point de grande masse, pour définir théoriquement le trou noir sans rotation. Le scientifique allemand a également calculé le rayon du trou noir obtenant la même valeur que Laplace. La surface sphérique définie par le rayon est appelée limite d'événements et tout ce qui est à l'intérieur constitue un trou noir.

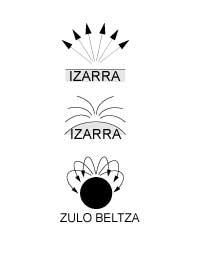
Par conséquent, il n'est pas possible de sortir de lui. Quant au parcours de la lumière, les différentes situations décrites dans la figure 2 nous aideront à comprendre le problème. Si on considère le cas d'une première étoile simple, (a), le champ de gravité ne sera pas très fort et la lumière échappera en suivant le parcours correct. Si nous considérons que l'étoile se contracte, (b), la même masse s'accumule dans un volume inférieur et les rayons sortent, mais s'écartant par le chemin droit. En bref (c), les rayons se pencheront complètement, retournant à la surface qui ont été reproduites (dans le cas du trou noir).

Cependant, les trous noirs ne pouvaient pas dire s'ils existaient ou non dans l'Univers tel que défini mathématiquement par Mitchel, Laplace ou Schwarzschill. Ensuite, les travaux d'astrophysique ont été ceux qui ont abordé le problème, mais les contributions des astrophysiciens seront discutés dans le prochain numéro.

ÉPHÉMÉRIDES SOLEIL: Le 18 février, il entre en Poissons à 15h 35m (UT). LUNE QUART CROISSANT PLEINE LUNE QUATRIÈME MENGUANTE QUART CROISSANT jour (UT) 623 h 55 min 1314 h 57 min 2113h 5min —---- PLANÈTES MERCURE: il est allongé au maximum le 21 février. Par conséquent, nous pouvons le voir au crépuscule dans ceux qui sont autour de ce jour. VÉNUS: Après avoir passé le mois précédent pour son allongement maximum, nous pourrons très bien le voir au crépuscule. Le 24 février son éclat est maximal, bien que ce jour soit proche de la Lune pour ne pas la voir très bien. MARTITZ: Après avoir passé l’opposition le mois précédent, nous pouvons encore le voir haut dès qu’il obscurcira. JUPITER: le mois prochain sera en opposition, donc nous l'aurons déjà en bon état à minuit et chaque jour plus tôt. SATURNE: il est en conjonction le 9 février, c'est-à-dire que nous ne pourrons pas le voir tout le mois.