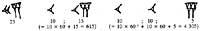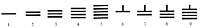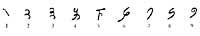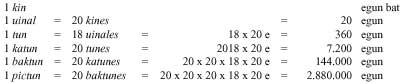Historia das cifras (IV)

1990/07/01 Angulo, Patxi Iturria: Elhuyar aldizkaria

• Matematika

Nos sistemas de numeración que vimos até agora as cifras tiñan un valor fixo. No sistema chinés escribíase o símbolo da orde entre os valores de diferente orde.

Paso decisivo

Nos sistemas de numeración que vimos até agora as cifras tiñan un valor fixo. A cifra romana L, por exemplo, en calquera lugar, custará sempre 50. No noso sistema non: No 79876 o primeiro sete da esquerda toma o valor 70.000 e o outro o valor 70, é dicir, o valor dunha cifra depende da posición. A isto denomínaselle principio de posición.

Sistema

chinés

entre valores de distinta orde

escribíase o símbolo da orde.

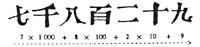
Até conseguir este principio o home deu moitas voltas ás cifras.

Esta regra básica foi inventada polos babilonios. A principios do ano 2000. Na época do rei Hamurabi (a. C. 1792-1750) foi un dos primeiros astrónomos e matemáticos babilónicos en crear un sistema de numeración. O valor da cifra variaba segundo a posición. Escribían os números na base sexagesimal mediante dous símbolos

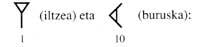
Números do 1 ao 59 por principio aditivo e a partir de aí por principio de posición. A pesar de que este sistema era similar ao noso, en cada orde de unidades utilizaba o principio aditivo e non utilizaban símbolos diferentes paira representar números até 59. Isto suscitou moitas dúbidas. Pero esta dificultade oculta outra máis profunda

ten. Como indicar que non se necesitan cifras nunha orde de unidades? É dicir, como escribir os números 203, 1003? Se se quere utilizar o principio de posición, débese escribir en 3 en primeiro lugar, 2 no terceiro e 2 no segundo. Os babilonios aínda non coñecían este concepto. 1200 anos.

Ao principio deixaban un oco entre dúas ordes

Pero isto non foi una solución adecuada. Por último, a. C. III. No século XX inventouse outro símbolo paira expresar a ausencia de orde

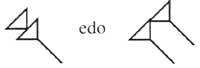
Este é o cero máis antigo. Pero isto non o tomaron como un número, senón no sentido do baleiro.

Dous mil anos despois os chineses erixiron esta regra. Alí durante a dinastía (a.C.) II - d.C. III. séculos) inventaron un sistema de raias horizontais e verticais.

A liña horizontal valorábase en 5. A partir de aí os números representábanse segundo o principio de posición:

Este sistema tivo un problema: cando as cifras dun número escribíanse só con liñas verticais (434), non se podía saber que número era (344, 443, 2324, ...). Máis tarde intercambiaron liñas horizontais e verticais entre si, e máis tarde mesturáronse estes dous sistemas, representando ordes sucesivas con diferentes sistemas: unidades, porcentaxes, dez mil, ... escribindo con liñas verticais e outros, dez, mil, ... con liñas horizontais. Solucionáronse algúns problemas. Con todo, paira comprender o concepto cero houbo séculos de existencia.

Paira expresar a falta dunha orde, algúns deixaban un oco. Isto non foi un bo camiño e finalmente valeuse do símbolo da tradicional numeración chinesa. Outros anotaron os números dentro duns cadros, deixando a casa da orde que faltaba. Pero C. III. Até o século XX non conseguiron o cero. Logrouse grazas á influencia de matemáticos e astrónomos hindús.

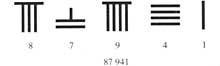
Séculos despois, en Centroamérica os mayas conseguiron os mesmos avances. No primeiro milenio da era cristiá alcanzaron a cima da súa sociedade en moitos campos: arte, escultura, arquitectura, matemáticas, educación, ... En astronomía, por exemplo, obtiveron datos máis precisos que os europeos; en matemáticas tamén coñecían o principio de posición e o cero.

Codex de Dresde (IX. No século XX, os mayas sazerdote tiñan aínda un sistema de base vinte (con cero e con principio de posición).

Segundo este sistema, o dezanove primeiros números escribíanse en puntos e raias. A partir de aí os números representábanse por columnas. Nas columnas había tantas plantas como orde. Unidades paira números de dúas ordes no inferior e de vinte no superior. Tres

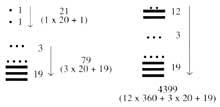
nas de orde, na terceira planta non se escribían as catro porcentaxes, senón os de 360. Nas seguintes plantas seguiuse a base de vinte. Por iso, as da 4ª planta son múltiplos de 7.200, as da 5ª son múltiplos de 144.000, ... Para que as cifras garden o seu lugar cando faltaba unha orde, inventaron o cero.

Ao principio, xunto coas cifras, escribían os símbolos da súa orde. Máis tarde déronse conta de que estes símbolos non eran necesarios e retiráronos. A razón da orde 360 da terceira planta hai que buscala en astronomía. Nos calendarios mayas a primeira planta indica os días, a segunda os meses (20 días), a terceira os anos (360 días), ...

Estes son os primeiros pobos que crearon a cifra cero e o principio de posición. Con todo, non souberon sacar proveito. Durante os dous mil anos que utilizaron o sistema aos babilonios non se lles ocorreu asociar cada cifra a un signo especial; os chineses seguiron utilizando a escritura ideográfica e os mayas escribían os números cun principio aditivo.

Grazas ao cero, os babilonios conseguiron notables avances, xa que o utilizaban como axente aritmético. Os mayas, pola súa singularidade na terceira planta, non puideron aplicar os avances nas operacións. Grazas a estas deficiencias, estes sistemas non serviron paira operar.

Sistema de numeración moderno

Estamos cerca do sistema de numeración moderno. Quen ten a honra de ser inventor do noso sistema?

A principios deste século algúns historiadores deron esa honra aos gregos. Pero non hai ningún documento que o demostre. Como vimos antes, os gregos utilizaron ao longo da historia dous sistemas: un equivalente ao sistema romano e outro alfabético. En ningún dos dous casos a cifra era cero. Mesmo descoñecían o principio de posición.

Beizos

sen os matemáticos hindús merecen a honra. Norte da India. O antepasado do noso sistema naceu cara ao século V.

A antiga numeración hindú parecía ás que vimos, pero tiña xa una característica do sistema moderno: as nove cifras representábanse con distintos símbolos. Con todo, paira escribir un número utilizaban o principio aditivo. Por tanto, atoparon límites similares. Como non podían escribir números grandes, ocorréuselles escribir con todas as letras:

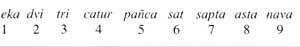
O nove primeiros números tiñan un nome especial. Puxeron nomes especiais a Hamarra e as súas verduras. Os outros números escribíanse con nomes compostos. Eles utilizaban unha orde crecente de esquerda a dereita. Entre as unidades e decimais paira escribir un número se intercalaba o nome de dez, entre dez e cen o nome do tecido, etc.

Debido ao costume e por necesidade breve, matemáticos e astrónomos hindús eliminaron os nomes da base e as súas verduras, mantendo a orde. Deste xeito obtiveron una numeración de posición verbal. Este avance supuxo outro: déronse conta de que necesitaban algo paira expresar a falta dunha orde. Paira iso utilizouse a palabra sunya (baleiro). Agora si tiñan os tres alicerces do sistema moderno:

• diferentes cifras paira números do 1 ao 9
• principio de posición
• cero

Con todo, tiñan que superar un obstáculo. O seu novo sistema, incluído o cero, era verbal. As dúas últimas bases, segundo os documentos coñecidos, como moi tarde en C. Xa sabían no século V. O 25 de agosto de 458 do Calendario Juliano, publicado polos membros do movemento relixioso hindú divino no tratado chamado Lokavibbar, aparece o número 14236713:

triny ekam sapta sat trini dve catvary ekakam

(literalmente tres sete seis tres catro)

É de destacar que xunto a cada enunciado aparece a palabra sthanakramad (literalmente: en orde de posición) como axuda paira non expertos. Outra mención especial: paira non aburrirse da repetición dunha cifra nun número utilizaron os sinónimos do nome de devandita cifra:

Isto poetizó as matemáticas e facilitou a memorización do cálculo.

Sabemos que os aritméticos hindús eran moi hábiles no cálculo. Pero antes de aplicar a base do noso cálculo (como noutros países) utilizáronse diferentes ferramentas (ábaco, táboa de cálculo, ...). Os hindús representaban o ábaco de columna na area. Na primeira columna da dereita as unidades, na segunda as decenas, na terceira as porcentaxes, etc. utilizando as cifras antigas que escribían. Pero este método era molesto e difícil.

d. C. VIN. A principios do século XX mesturáronse as numeracións oral e escrita, ao imporse á outra as vantaxes da numeración oral. Ao mesmo tempo, seguindo a imaxe do ábaco, cambiaron o sentido da escritura dos números. O cero expresouse cun punto ou cun pequeno círculo por motivos descoñecidos. Aos poucos fóronse introducindo cambios importantes. Ademais acurtáronse e melloraron as regras. Grazas ao seu tesón, os hindús conseguiron hai quince séculos una técnica de operación tan sinxela e rápida como a actual.

Con todo, debían dar o último paso: a normalización do concepto abstracto cero, xa que até entón o baleiro, a columna, ou o espazo baleiro, tiña significado. Como todos os ceros anteriores utilizábase paira encher ocos. Pero os hindús foron capaces de superar esta barreira e, a mediados de século, o cero tiña significado baleiro e nada.

Grazas a iso, nun traballo datado no ano 628, o matemático e astrónomo Brahmagupta demostrou como as seis operacións básicas (suma, resta, multiplicación, división, potencias e raíces) podían realizarse co patrimonio, a débeda e a nada (é dicir, con números positivos, negativos e nulos). Naceu o algebra moderno.