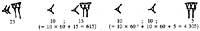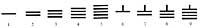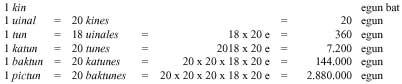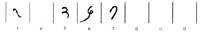History of figures (IV)

1990/07/01 Angulo, Patxi Iturria: Elhuyar aldizkaria

• Matematika

In the numbering systems we have seen so far the figures had a fixed value. In the Chinese system the command symbol was written between the values of different order.

Decisive step

In the numbering systems we have seen so far the figures had a fixed value. The Roman figure L, for example, anywhere, will always cost 50. In our system no: In 79876 the first seven on the left takes the value 70,000 and the other the value 70, that is, the value of a figure depends on the position. This is called the position principle.

System

chinese

between different order values

the symbol of order was written.

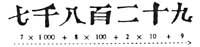
Until this principle was achieved, man made many turns to the figures.

This basic rule was invented by the Babylonians. At the beginning of 2000. At the time of King Hamurabi (a. C. 1792-1750) was one of the first Babylonian astronomers and mathematicians to create a numbering system. The value of the figure varied according to the position. Wrote numbers on the sexagesimal basis by two symbols

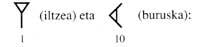
Numbers 1 to 59 by additive principle and thereafter by position principle. Although this system was similar to ours, in each order of units it used the additive principle and did not use different symbols to represent numbers up to 59. This raised many doubts. But this difficulty conceals another deeper

has. How to indicate that no numbers are needed in an order of units? That is, how to write numbers 203, 1003? If you want to use the position principle, you should write in 3 first, 2 in the third and 2 in the second. The Babylonians still did not know this concept. 1200 years.

At first they left a gap between two orders

But this was not an adequate solution. Finally, a. C. III. In the twentieth century another symbol was invented to express the absence of order

This is the oldest zero. But this was not taken as a number, but in the sense of emptiness.

Two thousand years later the Chinese erected this rule. There during the dynasty (BC) II - d.C. III. centuries) invented a system of horizontal and vertical stripes.

The horizontal line was valued at 5. From there the numbers were represented according to the position principle:

This system had a problem: when the numbers of a number were written only with vertical lines (434), one could not know what number it was (344, 443, 2324,...). Later they exchanged horizontal and vertical lines with each other, and later these two systems were mixed, representing successive orders with different systems: units, percentages, ten thousand, .. writing with vertical lines and others, ten, thousand, .. with horizontal lines. Some problems were solved. However, to understand the concept zero there were centuries of existence.

To express the lack of an order, some left a gap. This was not a good path and finally used the symbol of the traditional Chinese numbering. Others scored the numbers within a few boxes, leaving the missing order box. But C. III. Until the twentieth century they did not get zero. It was achieved thanks to the influence of Hindu mathematicians and astronomers.

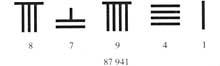
Centuries later, in Central America the Maya achieved the same advances. In the first millennium of the Christian era they reached the peak of their society in many fields: art, sculpture, architecture, mathematics, education,... In astronomy, for example, they obtained more precise data than the Europeans; in mathematics they also knew the principle of position and zero.

Dresden Codex (IX. In the 20th century, the Sazerdote Maya still had a base system of twenty (with zero and with beginning of position).

According to this system, the first nineteen numbers were written in points and stripes. From there the numbers were represented by columns. In the columns there were as many plants as order. Units for numbers of two orders in the lower and twenty in the upper. Three

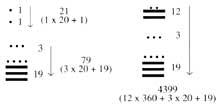
in those of order, in the third plant were not written the four percentages, but those of 360. In the following plants the base of twenty was followed. Therefore, those on the 4th floor are multiples of 7,200, those on the 5th are multiples of 144,000, ... For the figures to keep their place when an order was missing, they invented zero.

At first, along with the figures, they wrote the symbols of their order. Later they realized that these symbols were not necessary and removed them. The reason for the order 360 of the third floor must be sought in astronomy. In Mayan calendars the first floor indicates the days, the second the months (20 days), the third the years (360 days), ...

These are the first peoples who created the zero figure and the principle of position. However, they could not profit. During the two thousand years using the system, the Babylonians did not think of associating each figure to a special sign; the Chinese continued to use ideographic writing and the Mayans wrote the numbers with an additive principle.

Thanks to zero, the Babylonians made remarkable progress, since they used it as an arithmetic agent. The Maya, due to their uniqueness in the third floor, could not apply the advances in operations. Thanks to these shortcomings, these systems did not serve to operate.

Modern numbering system

We are close to the modern numbering system. Who has the honor of being an inventor of our system?

At the beginning of this century some historians gave that honor to the Greeks. But there is no document to prove it. As we have seen before, the Greeks used throughout history two systems: one equivalent to the Roman system and one alphabetic. In neither case the figure was zero. They even did not know the position principle.

Lips

without Hindu mathematicians deserve honor. North of India. The ancestor of our system was born around the 5th century.

The old Hindu numeration looked like the ones we have seen, but it already had a characteristic of the modern system: the nine figures were represented with different symbols. However, to write a number they used the additive principle. Therefore, they found similar limits. Since they could not write large numbers, they thought of writing with all the letters:

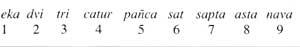
The first nine numbers had a special name. They put special names on Hamarra and her vegetables. The other numbers were written with compound names. They used a growing order from left to right. Between the units and decimals to write a number the name of ten was interspersed, between ten and a hundred the name of the fabric, etc.

Due to custom and brief necessity, Hindu mathematicians and astronomers removed the base names and their vegetables, keeping order. Thus they obtained a verbal position numbering. This advance meant another: they realized they needed something to express the lack of an order. The word sunya (empty) was used for this purpose. Now they did have the three pillars of the modern system:

• different numbers for numbers from 1 to 9
• position principle
• zero

However, they had to overcome an obstacle. His new system, including zero, was verbal. The last two bases, according to known documents, no later than C. They already knew in the 5th century. On August 25, 458 of the Julian Calendar, published by members of the divine Hindu religious movement in the treatise called Lokavibbar, the number 14236713 appears:

triny ekam sapta sat trini dve catvary ekakam

(literally three seven six three four)

It is noteworthy that alongside each statement appears the word sthanakramad (literally: in order of position) as an aid for non-experts. Another special mention: to avoid getting bored with the repetition of a figure in a number they used the synonyms of the name of that figure:

This poetized mathematics and facilitated the memorization of the calculus.

We know that Hindu arithmetics were very skilled in the calculation. But before applying the basis of our calculation (as in other countries) different tools were used (abacus, counting table, ..). The Hindus represented the column abacus in the sand. In the first column on the right the units, in the second the tens, in the third the percentages, etc. using the old figures they wrote. But this method was annoying and difficult.

d. C. VI. At the beginning of the twentieth century oral and written numerations were mixed, imposing on the other the advantages of oral numbering. At the same time, following the image of the abacus, they changed the meaning of the writing of the numbers. Zero was expressed with a point or a small circle for unknown reasons. Important changes were gradually introduced. The rules were also shortened and improved. Thanks to their determination, the Hindus achieved fifteen centuries ago a technique of operation as simple and fast as the current one.

However, they had to take the last step: the normalization of the abstract concept zero, since until then the void, the column, or the empty space, had meaning. Like all previous zeros it was used to fill gaps. But the Hindus were able to overcome this barrier and, in the middle of the century, zero had empty meaning and nothing.

Thanks to this, in a work dated 628, the mathematician and astronomer Brahmagupta demonstrated how the six basic operations (addition, subtraction, multiplication, division, powers and roots) could be performed with heritage, debt and nothingness (i.e., with positive, negative and null numbers). Modern algebra was born.