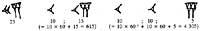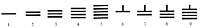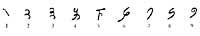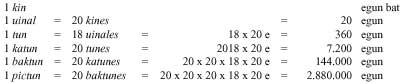Histoire des chiffres (IV)

1990/07/01 Angulo, Patxi Iturria: Elhuyar aldizkaria

• Matematika

Dans les systèmes de numérotation que nous avons vu jusqu'ici les chiffres avaient une valeur fixe. Dans le système chinois était écrit le symbole de l'ordre entre les valeurs d'ordre différent.

Étape décisive

Dans les systèmes de numérotation que nous avons vu jusqu'ici les chiffres avaient une valeur fixe. Le chiffre romain L, par exemple, n'importe où, coûtera toujours 50. Dans notre système non: En 79876 le premier sept de la gauche prend la valeur 70.000 et l'autre la valeur 70, c'est-à-dire la valeur d'un chiffre dépend de la position. On l'appelle principe de position.

Système

chinois chinois chinois chinois chinois chinois chinois chinois chinois chinois chinois chinois chinois

entre les valeurs d'ordre différent

On écrivait le symbole de l'ordre.

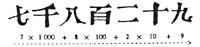
Jusqu'à ce principe l'homme a donné beaucoup de tours aux chiffres.

Cette règle de base a été inventée par les Babyloniens. Début 2000. À l'époque du roi Hamurabi (a. C. 1792-1750) a été l'un des premiers astronomes et mathématiciens babyloniens à créer un système de numérotation. La valeur du chiffre variait selon la position. Ils écrivaient les nombres à la base sexagésimale par deux symboles

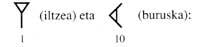
Nombres de 1 à 59 par principe additif et de là par principe de position. Bien que ce système soit similaire au nôtre, chaque ordre d'unités utilise le principe additif et n'utilise pas de symboles différents pour représenter des nombres jusqu'à 59. Cela suscita beaucoup de doutes. Mais cette difficulté cache une autre plus profonde

a. Comment indiquer que les chiffres ne sont pas nécessaires dans un ordre d'unités? Autrement dit, comment écrire les numéros 203, 1003? Si vous voulez utiliser le principe de position, vous devez écrire en 3 en premier, 2 en troisième et 2 en second. Les Babyloniens ne connaissaient pas encore ce concept. 1200 ans.

Au début, ils laissaient un écart entre deux ordres

Mais ce n'était pas une solution adéquate. Enfin, a. C. III. Au XXe siècle, un autre symbole a été inventé pour exprimer l'absence d'ordre

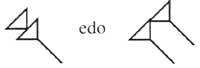
C'est le plus ancien zéro. Mais cela ne l'a pas pris comme un nombre, mais dans le sens du vide.

Deux mille ans plus tard les Chinois ont érigé cette règle. Là pendant la dynastie (a.C.) II - d.C. III. siècles) inventé un système de rayures horizontales et verticales.

La ligne horizontale était évaluée à 5. De là, les nombres étaient représentés selon le principe de position:

Ce système a eu un problème: lorsque les chiffres d'un numéro étaient écrits uniquement avec des lignes verticales (434), on ne pouvait pas savoir quel nombre était (344, 443, 2324, ...). Plus tard, ils échangèrent des lignes horizontales et verticales entre eux, et plus tard se mêlèrent ces deux systèmes, représentant des ordres successifs avec différents systèmes: unités, pourcentages, dix mille, ... écrivant avec des lignes verticales et autres, dix, mille, ... avec des lignes horizontales. Certains problèmes ont été résolus. Cependant, pour comprendre le concept zéro il y avait des siècles d'existence.

Pour exprimer le manque d'ordre, certains laissaient un trou. Ce n'était pas un bon chemin et a finalement été validé par le symbole de la numérotation traditionnelle chinoise. D'autres ont noté les nombres dans des images, laissant la case de l'ordre manquant. Mais C. III. Jusqu'au 20ème siècle, ils n'ont pas obtenu le zéro. Il a été accompli grâce à l'influence des mathématiciens et des astronomes hindouistes.

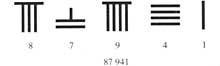
Des siècles plus tard, en Amérique centrale, les Mayas ont obtenu les mêmes progrès. Dans le premier millénaire de l'ère chrétienne, ils ont atteint le sommet de leur société dans de nombreux domaines: l'art, la sculpture, l'architecture, les mathématiques, l'éducation, ... En astronomie, par exemple, ils ont obtenu des données plus précises que les Européens; en mathématiques, ils ont également connu le principe de position et zéro.

Codex de Dresde (IX. Au XXe siècle, les Mayas sazerdote avaient encore un système de base vingt (avec zéro et avec principe de position).

Selon ce système, les dix-neuf premiers numéros étaient écrits en points et rayures. De là, les nombres étaient représentés par des colonnes. Dans les colonnes il y avait autant de plantes comme ordre. Unités pour les nombres de deux ordres dans le inférieur et de vingt dans le supérieur. Trois

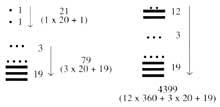
dans l'ordre, au troisième étage n'étaient pas écrits les quatre pourcentages, mais ceux de 360. Dans les plantes suivantes, la base de vingt a été suivie. Ainsi, celles du 4ème étage sont des multiples de 7200, celles du 5ème sont des multiples de 144.000, ... Pour que les chiffres gardent leur place quand un ordre manquait, ils ont inventé le zéro.

Au début, avec les chiffres, ils ont écrit les symboles de leur ordre. Plus tard, ils ont réalisé que ces symboles n'étaient pas nécessaires et les ont retirés. La raison de l'ordre 360 du troisième étage doit être recherchée en astronomie. Dans les calendriers mayas le premier étage indique les jours, le deuxième les mois (20 jours), le troisième les années (360 jours), ...

Ce sont les premiers peuples qui ont créé le chiffre zéro et le principe de position. Cependant, ils n'ont pas su profiter. Pendant les deux mille ans qu'ils utilisèrent le système aux Babyloniens, il ne leur vint pas d'associer chaque chiffre à un signe spécial ; les Chinois continuèrent à utiliser l'écriture idéographique et les Mayas écrivirent les nombres avec un principe additif.

Grâce au zéro, les Babyloniens ont réalisé des progrès remarquables, puisqu'ils l'utilisaient comme agent arithmétique. Les Mayas, par leur singularité au troisième étage, n'ont pas pu appliquer les progrès dans les opérations. Grâce à ces lacunes, ces systèmes n'ont pas servi à fonctionner.

Système de numérotation moderne

Nous sommes près du système de numérotation moderne. Qui a l'honneur d'être inventeur de notre système?

Au début de ce siècle, certains historiens ont donné cet honneur aux Grecs. Mais il n'y a aucun document qui le prouve. Comme nous l'avons vu auparavant, les Grecs utilisèrent au cours de l'histoire deux systèmes : un équivalent au système romain et un autre alphabétique. Dans aucun des deux cas, le chiffre était nul. Ils ne connaissaient même pas le principe de position.

Lèvres, lèvres, lèvres

sans les mathématiciens hindous méritent l'honneur. Nord de l'Inde. L'ancêtre de notre système est né vers le cinquième siècle.

L'ancienne numérotation hindoue ressemblait à celle que nous avons vue, mais elle avait déjà une caractéristique du système moderne : les neuf chiffres étaient représentés par différents symboles. Cependant, pour écrire un nombre ils utilisaient le principe additif. Ils ont donc trouvé des limites similaires. Comme ils ne pouvaient pas écrire de grands nombres, il leur vint d'écrire avec toutes les lettres:

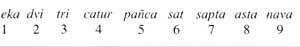
Les neuf premiers numéros avaient un nom spécial. Ils ont donné des noms spéciaux à Hamarra et à ses légumes. Les autres numéros étaient écrits avec des noms composés. Ils utilisaient un ordre croissant de gauche à droite. Parmi les unités et décimales pour écrire un numéro, on intercalait le nom de dix, entre dix et cent le nom du tissu, etc.

En raison de la coutume et par nécessité brève, mathématiciens et astronomes hindous ont supprimé les noms de la base et leurs légumes, en gardant l'ordre. Ils ont ainsi obtenu une numérotation de position verbale. Cette avancée a été un autre: ils ont réalisé qu'ils avaient besoin de quelque chose pour exprimer le manque d'un ordre. Pour cela, le mot sunya (vide) a été utilisé. Maintenant, ils avaient les trois piliers du système moderne:

• différents chiffres pour les nombres de 1 à 9
• début de position
• zéro zéro zéro zéro zéro zéro zéro zéro zéro zéro zéro zéro zéro zéro zéro zéro

Cependant, ils devaient surmonter un obstacle. Son nouveau système, y compris le zéro, était verbal. Les deux dernières bases, selon les documents connus, au plus tard en C. Ils savaient déjà au Ve siècle. Le 25 août 458 du Calendrier Julien, publié par les membres du mouvement religieux indien divin dans le traité appelé Lokavibbar, apparaît le numéro 14236713:

triny ekam sapta sat trini dve catvary ekakam

(littéralement trois sept six trois quatre)

A noter qu'à côté de chaque énoncé apparaît le mot sthanakramad (littéralement : en ordre de position) comme aide pour les non-experts. Une autre mention spéciale : pour ne pas s'ennuyer de la répétition d'un chiffre dans un nombre ont utilisé les synonymes du nom de ce chiffre :

Cela poétisa les mathématiques et facilita la mémorisation du calcul.

Nous savons que les arithmétiques hindous étaient très habiles dans le calcul. Mais avant d'appliquer la base de notre calcul (comme dans d'autres pays) différents outils ont été utilisés (abaque, tableau de comptage, ...). Les hindous représentaient l'abaque de colonne dans le sable. Dans la première colonne de droite les unités, dans la deuxième les dizaines, dans la troisième les pourcentages, etc. utilisant les chiffres anciens qui écrivaient. Mais cette méthode était ennuyeux et difficile.

d. d. C. VI. Au début du XXe siècle, les numérations orales et écrites ont été mélangées, imposant à l'autre les avantages de la numérotation orale. En même temps, suivant l'image de l'abaque, ils changèrent le sens de l'écriture des nombres. Le zéro a été exprimé avec un point ou un petit cercle pour des raisons inconnues. Peu à peu, des changements importants ont été introduits. De plus, les règles ont été raccourcies et améliorées. Grâce à leur teson, les hindous ont obtenu il y a quinze siècles une technique d'opération aussi simple et rapide que la technique actuelle.

Cependant, ils devaient faire le dernier pas: la normalisation du concept abstrait zéro, car jusqu'alors le vide, la colonne, ou l'espace vide, avait une signification. Comme tous les zéros précédents, il était utilisé pour remplir des trous. Mais les hindous ont pu surmonter cette barrière et, au milieu du siècle, le zéro avait une signification vide et rien.

Ainsi, dans un travail daté de 628, le mathématicien et astronome Brahmagupta démontra comment les six opérations de base (addition, soustraction, multiplication, division, puissances et racines) pouvaient être effectuées avec le patrimoine, la dette et le néant (c'est-à-dire avec des nombres positifs, négatifs et nuls). L'algèbre moderne est né.