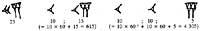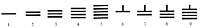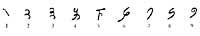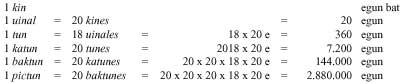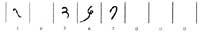Historia de las cifras (IV)

1990/07/01 Angulo, Patxi Iturria: Elhuyar aldizkaria

• Matematika

En los sistemas de numeración que hemos visto hasta ahora las cifras tenían un valor fijo. En el sistema chino se escribía el símbolo del orden entre los valores de diferente orden.

Paso decisivo

En los sistemas de numeración que hemos visto hasta ahora las cifras tenían un valor fijo. La cifra romana L, por ejemplo, en cualquier lugar, costará siempre 50. En nuestro sistema no: En el 79876 el primer siete de la izquierda toma el valor 70.000 y el otro el valor 70, es decir, el valor de una cifra depende de la posición. A esto se le denomina principio de posición.

Sistema

chino

entre valores de distinto orden

se escribía el símbolo del orden.

Hasta conseguir este principio el hombre dio muchas vueltas a las cifras.

Esta regla básica fue inventada por los babilonios. A principios del año 2000. En la época del rey Hamurabi (a. C. 1792-1750) fue uno de los primeros astrónomos y matemáticos babilónicos en crear un sistema de numeración. El valor de la cifra variaba según la posición. Escribían los números en la base sexagesimal mediante dos símbolos

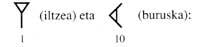
Números del 1 al 59 por principio aditivo y a partir de ahí por principio de posición. A pesar de que este sistema era similar al nuestro, en cada orden de unidades utilizaba el principio aditivo y no utilizaban símbolos diferentes para representar números hasta 59. Esto suscitó muchas dudas. Pero esta dificultad oculta otra más profunda

tiene. ¿Cómo indicar que no se necesitan cifras en un orden de unidades? Es decir, ¿cómo escribir los números 203, 1003? Si se quiere utilizar el principio de posición, se debe escribir en 3 en primer lugar, 2 en el tercero y 2 en el segundo. Los babilonios todavía no conocían este concepto. 1200 años.

Al principio dejaban un hueco entre dos órdenes

Pero esto no fue una solución adecuada. Por último, a. C. III. En el siglo XX se inventó otro símbolo para expresar la ausencia de orden

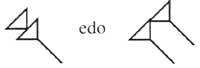
Este es el cero más antiguo. Pero esto no lo tomaron como un número, sino en el sentido del vacío.

Dos mil años después los chinos erigieron esta regla. Allí durante la dinastía (a.C.) II - d.C. III. siglos) inventaron un sistema de rayas horizontales y verticales.

La línea horizontal se valoraba en 5. A partir de ahí los números se representaban según el principio de posición:

Este sistema tuvo un problema: cuando las cifras de un número se escribían sólo con líneas verticales (434), no se podía saber qué número era (344, 443, 2324, ...). Más tarde intercambiaron líneas horizontales y verticales entre sí, y más tarde se mezclaron estos dos sistemas, representando órdenes sucesivas con diferentes sistemas: unidades, porcentajes, diez mil, ... escribiendo con líneas verticales y otros, diez, mil, ... con líneas horizontales. Se solucionaron algunos problemas. Sin embargo, para comprender el concepto cero hubo siglos de existencia.

Para expresar la falta de un orden, algunos dejaban un hueco. Esto no fue un buen camino y finalmente se valió del símbolo de la tradicional numeración china. Otros anotaron los números dentro de unos cuadros, dejando la casilla del orden que faltaba. Pero C. III. Hasta el siglo XX no consiguieron el cero. Se logró gracias a la influencia de matemáticos y astrónomos hindúes.

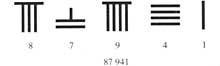
Siglos después, en Centroamérica los mayas consiguieron los mismos avances. En el primer milenio de la era cristiana alcanzaron la cima de su sociedad en muchos campos: arte, escultura, arquitectura, matemáticas, educación, ... En astronomía, por ejemplo, obtuvieron datos más precisos que los europeos; en matemáticas también conocían el principio de posición y el cero.

Codex de Dresde (IX. En el siglo XX, los mayas sazerdote tenían todavía un sistema de base veinte (con cero y con principio de posición).

Según este sistema, los diecinueve primeros números se escribían en puntos y rayas. A partir de ahí los números se representaban por columnas. En las columnas había tantas plantas como orden. Unidades para números de dos órdenes en el inferior y de veinte en el superior. Tres

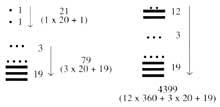
en las de orden, en la tercera planta no se escribían los cuatro porcentajes, sino los de 360. En las siguientes plantas se siguió la base de veinte. Por eso, las de la 4ª planta son múltiplos de 7.200, las de la 5ª son múltiplos de 144.000, ... Para que las cifras guarden su lugar cuando faltaba un orden, inventaron el cero.

Al principio, junto con las cifras, escribían los símbolos de su orden. Más tarde se dieron cuenta de que estos símbolos no eran necesarios y los retiraron. La razón del orden 360 de la tercera planta hay que buscarla en astronomía. En los calendarios mayas la primera planta indica los días, la segunda los meses (20 días), la tercera los años (360 días), ...

Estos son los primeros pueblos que crearon la cifra cero y el principio de posición. Sin embargo, no supieron sacar provecho. Durante los dos mil años que utilizaron el sistema a los babilonios no se les ocurrió asociar cada cifra a un signo especial; los chinos siguieron utilizando la escritura ideográfica y los mayas escribían los números con un principio aditivo.

Gracias al cero, los babilonios consiguieron notables avances, ya que lo utilizaban como agente aritmético. Los mayas, por su singularidad en la tercera planta, no pudieron aplicar los avances en las operaciones. Gracias a estas deficiencias, estos sistemas no sirvieron para operar.

Sistema de numeración moderno

Estamos cerca del sistema de numeración moderno. ¿Quién tiene el honor de ser inventor de nuestro sistema?

A principios de este siglo algunos historiadores dieron ese honor a los griegos. Pero no hay ningún documento que lo demuestre. Como hemos visto antes, los griegos utilizaron a lo largo de la historia dos sistemas: uno equivalente al sistema romano y otro alfabético. En ninguno de los dos casos la cifra era cero. Incluso desconocían el principio de posición.

Labios

sin los matemáticos hindúes merecen el honor. Norte de la India. El antepasado de nuestro sistema nació hacia el siglo V.

La antigua numeración hindú parecía a las que hemos visto, pero tenía ya una característica del sistema moderno: las nueve cifras se representaban con distintos símbolos. Sin embargo, para escribir un número utilizaban el principio aditivo. Por tanto, encontraron límites similares. Como no podían escribir números grandes, se les ocurrió escribir con todas las letras:

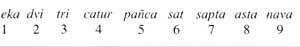
Los nueve primeros números tenían un nombre especial. Pusieron nombres especiales a Hamarra y sus verduras. Los otros números se escribían con nombres compuestos. Ellos utilizaban un orden creciente de izquierda a derecha. Entre las unidades y decimales para escribir un número se intercalaba el nombre de diez, entre diez y cien el nombre del tejido, etc.

Debido a la costumbre y por necesidad breve, matemáticos y astrónomos hindúes eliminaron los nombres de la base y sus verduras, manteniendo el orden. De este modo obtuvieron una numeración de posición verbal. Este avance supuso otro: se dieron cuenta de que necesitaban algo para expresar la falta de un orden. Para ello se utilizó la palabra sunya (vacío). Ahora sí tenían los tres pilares del sistema moderno:

• diferentes cifras para números del 1 al 9
• principio de posición
• cero

Sin embargo, tenían que superar un obstáculo. Su nuevo sistema, incluido el cero, era verbal. Las dos últimas bases, según los documentos conocidos, a más tardar en C. Ya sabían en el siglo V. El 25 de agosto de 458 del Calendario Juliano, publicado por los miembros del movimiento religioso hindú divino en el tratado llamado Lokavibbar, aparece el número 14236713:

triny ekam sapta sat trini dve catvary ekakam

(literalmente tres siete seis tres cuatro)

Es de destacar que junto a cada enunciado aparece la palabra sthanakramad (literalmente: en orden de posición) como ayuda para no expertos. Otra mención especial: para no aburrirse de la repetición de una cifra en un número utilizaron los sinónimos del nombre de dicha cifra:

Esto poetizó las matemáticas y facilitó la memorización del cálculo.

Sabemos que los aritméticos hindúes eran muy hábiles en el cálculo. Pero antes de aplicar la base de nuestro cálculo (como en otros países) se utilizaron diferentes herramientas (ábaco, tabla de conteo, ...). Los hindúes representaban el ábaco de columna en la arena. En la primera columna de la derecha las unidades, en la segunda las decenas, en la tercera los porcentajes, etc. utilizando las cifras antiguas que escribían. Pero este método era molesto y difícil.

d. C. VI. A principios del siglo XX se mezclaron las numeraciones oral y escrita, al imponerse a la otra las ventajas de la numeración oral. Al mismo tiempo, siguiendo la imagen del ábaco, cambiaron el sentido de la escritura de los números. El cero se expresó con un punto o con un pequeño círculo por motivos desconocidos. Poco a poco se fueron introduciendo cambios importantes. Además se acortaron y mejoraron las reglas. Gracias a su tesón, los hindúes consiguieron hace quince siglos una técnica de operación tan sencilla y rápida como la actual.

Sin embargo, debían dar el último paso: la normalización del concepto abstracto cero, ya que hasta entonces el vacío, la columna, o el espacio vacío, tenía significado. Como todos los ceros anteriores se utilizaba para rellenar huecos. Pero los hindúes fueron capaces de superar esta barrera y, a mediados de siglo, el cero tenía significado vacío y nada.

Gracias a ello, en un trabajo fechado en el año 628, el matemático y astrónomo Brahmagupta demostró cómo las seis operaciones básicas (suma, resta, multiplicación, división, potencias y raíces) podían realizarse con el patrimonio, la deuda y la nada (es decir, con números positivos, negativos y nulos). Nació el algebra moderno.