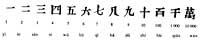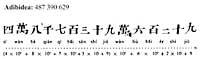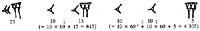History of figures (III)

1990/06/01 Angulo, Patxi Iturria: Elhuyar aldizkaria

• Matematika

Advancing

The initial numerical systems were based on the additive principle, that is, repeated as many times as necessary to represent a number (symbols). For example, number 2619 in some systems would need eighteen symbols. These systems did not meet the needs of accountants. Therefore, from the time of the ancient Empire (a. C.) XXVIII - XXIII. centuries) Egyptian scribes tried to facilitate writing until they got the so-called hieratic numbering

...

The new forms of the figures hardly remembered the initials. To write the number 2619, only the symbols corresponding to the numbers 2000, 600, 10 and 9 should be written.

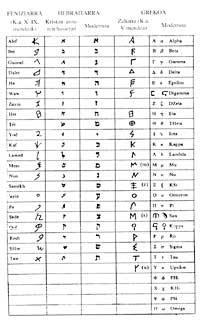
Two thousand years later, the Israeli scribes and the Greek mathematicians came up with the same thing, but this time, without schematizing the symbols, the numbers were adapting the letters of the alphabet.

Alphabet A.C. Around 1500 the Phoenicians invented Syria on the Palestinian coast. In the East it was transmitted to the peoples of Moa?a, Edomar, Ammonar and Hebrew. Also the Aramese nomads, who in the Middle East scattered him from Egypto to India. BC. IX. From the twentieth century it spread throughout the Mediterranean, being approved by the western peoples in a progressive way.

Twenty-six Phoenician letters created the Paleo-Hebrew and Aramean writing (from which they derived palminium, nabatar, syriar, Arabic, Persian, Turkish and Hindu alphabet). It was also the basis of the Greek alphabet. Greek is the first alphabet to introduce strict script of vowels. The latter was suggestive of the Etruscan alphabet, later Latin, and later of the Gothic, Georgian, Armenian and Cyrillic. It should be noted that all customs have preserved for centuries the names and order of the twenty-six letters.

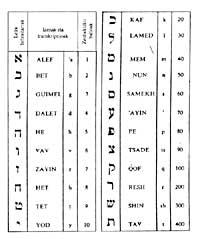
The Hebraitarians wrote the letters to write the numbers, starting from the right to the left and the largest. Between the last two symbols to separate the numbers from the words two quotes were written and when the figure was unique, in the upper left only a quotation mark.

But the maximum number they could write with this method was four hundred. Despite seeking solutions, they did not make great progress. They facilitated writing until number 999.999 and from there the obstacles did not disappear.

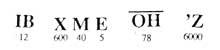
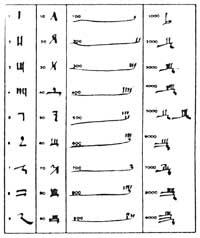
The Greek arithmetics also came up with representing numbers in letters. The classic alphabet was added the signs digamma, san and qopp a.

The intermediate numbers were written with letters together. To distinguish between words and numbers within a text, they were topped with a horizontal line. They wrote a quote on the top and left of the unit's letters to write numbers from 1,000 to 9,000.

We do not know which of these two systems is the oldest, between Hebrew and Greek. The oldest are the Greeks, Elephantine papyri (a. C.) 331-330) and coins of Ptolemy II Philadelphian (BC) 286-246). The Hebrans, for their part, are the coins of the Asmonean dynasty the oldest; a. C. 78. However, this does not mean any antiquity.

The main advantage of this alphabetic writing was the summary of writing. The number 479 was written in three figures (letters). However, most of the countries mentioned continued to use the additive principle. Therefore, the resources of their written numbering remained limited.

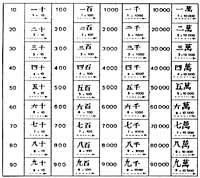
The people looking for a different solution were Chinese. These had thirteen special symbols.

In fact symbols are not figures, but normal images of Chinese writing. They indicate not only the graphic value, but also the phonetic value that corresponds to the names of Chinese numbers. Although today the various symbols are used according to Chinese notation, they are also pronounced. The illustrations of the previous figure are of the kaish-u type, the most widespread today, the simplest and oldest of the contemporaries (IV. It remains as used in the 19th century).

Another way they use is the official figures. It is more complicated than the previous one, used in official papers and arises to avoid fraud. The third form, called xíngshu, arises to summarize and accelerate writing. It is used in scribes, sketches, etc. With the excess of abbreviations, the above symbols became an excessively summary graph called caoshu, which only experts understood. Finally we have figures called ngán mà o gán mà zí (secret marks), used in cryptography. They are also used by traders.

In all forms the same numbering principle is used to express numbers. Multiples of the tenth are written using the multiplication principle and intermediate numbers combine the multiplication and sum principles. This principle had two main advantages: the symbols were not repeated so many times and in memory we had to keep fewer different symbols. Thanks to this they managed to write large numbers with few symbols (from 1 to 999 999 999 999 999 999 999 999 999 999 999 999 999 999 999 999 999 999). However, this method did not facilitate the calculation of operations, which were performed in abacus, table, rule, ...