History of figures (I)
1990/04/01 Angulo, Patxi Iturria: Elhuyar aldizkaria
Prehistory Prehistory
Human beings of old used the senses to express quantities that, like some animals, were not able to distinguish large quantities (as we do not understand today the quantity of three trillion).
The first numbers that were invented were one and two. One to express oneself (within a group). Also to express the penis (to differentiate from women) or man (to differentiate from animals).
Bia was an expression of duplicity (empowerment and manhood, life and death, truth and false, good and evil, etc. ).
In general, it can be said that from there (two) to separate larger quantities no special symbols were used and when they had to represent large quantities the same symbol was used, regardless of quantity. Their witnesses can be found in several languages of their environment: in the French they are similar trois (three) and très (very), in the English three (three) and throng (one machine), in the Latin only the first four numbers were declined.
It could be said, therefore, that at that time “the human capacity in terms of the understanding of the numbers did not pass by four.” This should not surprise us if we take into account that, at first glance, we are not able to guess how many cars there are in a row.
How did the first inhabitants learn to count? To answer this question it is necessary to distinguish and understand the two forms of numbers: cardinal and ordinal. Below is an example: If we say “It has 28 days of February” we speak of the number of days of February. Therefore, number 28 indicates a cardinal. On the contrary, if we say “today is February 28”, today we are saying it is February 28. Therefore, we indicate the order, that is, the ordinal form.
At first they used the method of pairing, that is, on a stick that blew for each grain, or they took a stone, or touched a part of the body. But that wasn't a big breakthrough. And it is that when they had to recount the same thing they had to redo bleeding. For example, when a flock of sheep went out in the morning and kept it in the afternoon, they had to count to know if any had been lost.
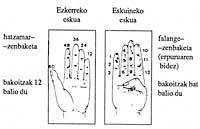
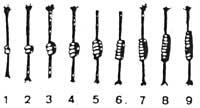
The Papuans of New Guinea used the body to quantify at the beginning of this century. Each part of the body indicated a number and to count it up to a number, maintaining the order in which the parts corresponding to all the previous numbers were touched. For example, to count 10 they played the chip (1) of the right hand, the tenant (2), the middle (3), the index (4) and the thumb (5), then the wrist (6), the elbow (7), the shoulder (8), the ear (9) and the eye (10). But if once they had done this they meant that they had counted 10, they did not touch the right eye directly, but began with the chip (1). This tells us that they had no abstract idea of numbers.
The exposed here is applicable to the old neighbors and without lips we can say that the body was the first support of arithmetic. It is the habit of having fingers of hands that still survive.
We could say that with these techniques they also learned to count at the same time that they learned to differentiate both forms. It was demonstrated that the differentiation capacity was human. We use both forms so often that we often forget the difference.
Invention of bases
Once the separation capacity was achieved, they found another problem: stones, sticks, notches, etc., which could not count large quantities. Continuous use. The solution was not, on the other hand, to give a special name to each number (number). Therefore, the human being was found in the need to express the greatest amounts of symbols at least.
To achieve this, different villages have invented different systems. The most widespread is base 10. Many peoples have used it, but how did they do it? To answer, let's put an example (he thinks they still did not know how to write): they took strips of different colors; white, blue, red… In the white strip of each animal they put a shell. In this strip when there were ten shells, they were pulled out and put one in the blue strip. In the white strip the shells were resumed. Then, when ten shells were accumulated in the blue strip, they were removed and put one on the red strip. Thus, when the animals finished they had two shells in red strip, six blue strips and three white strips, indicating the number of 263. All this was done without trust.
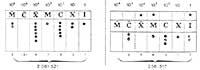
The test of the use of this system can be found in several languages, such as the Chinese oral numbering system:
Base 10 has an advantage over larger bases, its usefulness. But, why not have smaller bases? We should look in the statements for the reason: 4326 in two bases 11100110 As you know, more figures are needed.
But the use of base ten should not be sought in mathematical advantages, but in our hands. And it is that man has always used his hands to count, and in his hands there are ten fingers.
The ten base is not the only one that has been used. Bases five, twenty, twelve and sixty have also been used.
The reason why we use base 5 is found in the hand. For the count the fingers of one hand were used and the objects were grouped in five, that is, when in the left hand there were five raised fingers were lowered and in the right hand one was raised. So they could count up to twenty. The footprint of five bases can be found in several languages. For example, in the Api language of the New Hebrides

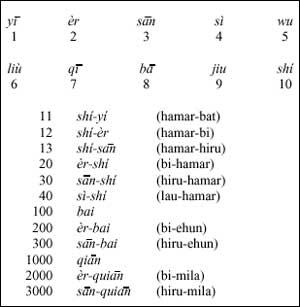
We can also find examples of twenty bases without going further, in Euskara. The first twenty numbers in Basque have a name and from there they are grouped in twenty:

Other examples: Maia, ...
The peoples who used this base also took into account the toes of the foot when counting.
The twelve base is wider than the previous one and has a great advantage over ten: The number 12 has divisors 2, 3, 4 and 6, facilitating the calculation for the division. We have the “dozen” and the “coarse” (12 dozen) that still live on this base. Among the villages that used this base are the Sumerian, Babylonian and Roman.
Its origin is unknown, but we should probably look for it in hand. And it is that, eliminating the thumb, in the other four fingers there are three phalange, forming a total of twelve phalange. This base is currently used in India, Pakistan, Afghanistan, Egypto, Syria, Turkey, etc.
Undoubtedly, the most enigmatic base is the sexagesimal. As a counting unit it becomes heavy. However, there are many peoples who have used it throughout history. We have his footprints. For example, time measurement is done in hours, minutes and seconds; the arches and angles are expressed in sixty bases by degrees, minutes and seconds.
The Sumerians were the first to use it. These passed to the Babylonian mathematicians and astronomers and these to the Greeks and Arabs.
There are different hypotheses about the origin of this base. One of them bases his argument on the union of two different civilizations. Let us think that if one used the base ten and the other the base twelve, if it collected both, according to this hypothesis, could reach the base sixty. In fact, the smallest multiple of the numbers 10 and 12 is 60.
Another possibility, in the same hypothesis, would be composed of five and twelve bases. The advantage of this case is the product of the numbers 60, 5 and 12. Therefore, we would not have to look for the smallest multiple of the commons. In addition, in the Sumerian language, evidence of the emergence of five bases can be found:

First calculators
Man, as he advanced in the use of the concept of number, tried to solve deeper problems. At the same time, the resources were improving. We can say that the most important function of the human being of that time was to facilitate wealth accounting.
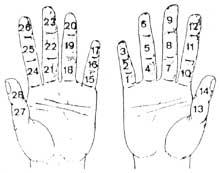
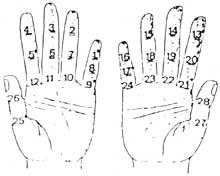
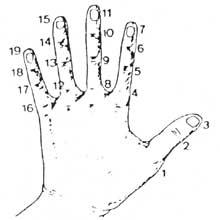
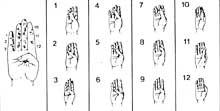
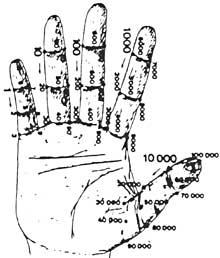
At first they had their hands. Therefore, we can consider that the first calculator was the hand. Although it does not seem so, ten billion can be counted with hands. Different methods were developed using falanges and joints between falanges. For their accounting, they put laces or other signals on the fingers or the number they played with the other hand. But the use of the hand was not limited to counting. They also performed manual calculations. For example, they knew how to multiply manually.
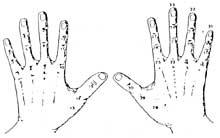

However, with the hands only indicated the numbers, but they could not keep them in memory. When relations between societies were accentuated with the development of trade, man found himself faced with another problem: how can I memorize what I had counted up to then?
It provided different methods and tools to address this problem. As an example, we will mention the “quipu” (knot) used by the cechueros. It had a main string to which other string groups joined, placed in regular sections. Although these tools met many other functions, they were mainly used to count. In the strings were made trabas of numbers (quantities). Currently this method can be found in: Siberia, Hawaii, Nigeria, New Mexico, etc.

Another prehistoric method was bone or wood. The oldest trace of the era “Aurignac” (a. C. C. We get between 35,000 and 20,000).
At first, the method consisted of making bleeding. Subsequently, different systems were improved and used. Each type of object was marked with a special symbol on the stick or bone. 150 years ago the archives were taken away in the Treasury Minister of Great Britain. XIX. At the beginning of the twentieth century the books of accounts in the French State, Switzerland, Germany, etc. were sticks (tayas). This method has been used as receipt, invoice or credit card in exchanges between trade and customer.
There is, however, another method that has influenced more arithmetic and accounting, is the accumulation of stones (stones, or sticks, shells, nuts, etc. ).
The accumulation of stones, together with the method of bleeding, indicates the grade 0 of counting, since it does not need an abstract discovery of numbers.
When the man began to use the bases, it was quite flexible to advance.


At present, the method of congestion in some tributes is used as a sign of differentiation and wealth. This method has helped man to form in the calculus. The word calculus comes from the Latin word “calculus”, whose meaning is “rounded stone”. The same etymology can be found in other languages: in Greek the word “pséphos” has meanings “numbers” and “a stone”; in Arabic the words “haswa” (reef) and “ihsa” (numbering, statistics) have the same root. Bowling is the origin of abacus and ball markers.
The first abacos were made in the soil by parallel ditches. Later on boards or stones, by parallel lines. Each ditch and line had a different value, being the value subject to the base. The stones, the calculus, and later the tiles, were placed on ditches and stripes, each of them took the value of the line or ditch.
On the East side, on the contrary, ball markers were created with the same function. Besides having these instruments, they could also perform operations. At present there is still a great custom of using the abacos in China, Japan, USSR and all the east.

Gai honi buruzko eduki gehiago
Elhuyarrek garatutako teknologia