The Creation of Science in Greece: A Pythagorean School
1986/04/01 Bandres Unanue, Luis Iturria: Elhuyar aldizkaria

While the dominant tendency of the Ionian school was the rationalist, what the Pythagorean schools took was a mystical tendency derived from orfism, which focused on observation and research.
Pitago (582-500 BC) was born in Samos, but around 530 he went to Southern Italy.
Those of this school sought a principle of intelligence which is the creator of the Universe. Aside from the tendency of the Ionian school based on the transformation of substance, this school established that, at the base of the material world, the only thing that the mind can acquire is the number.
Even though before the creation of this school, the Babylonians adapted to the bodies of amasado minute numerical proportions and Anaximadro himself spoke of room nine, eighteen and twenty times the thickness of the disc r, nine, eighteen and twenty times greater, the adaptation of numbers to all aspects of Nature is the result of a Pythagorean school.

We are used to using the idea of numbers (i.e., abstract quantities). We have no problem in five or a hundred figures, regardless of what they are, to be able to work. Hence, for both philosophy and mathematics, let us be aware of the difficulty involved in finding and isolating the unity of the concepts of the five, or of tissue, in groups of heterogeneous things, is really difficult.
In the field of mathematics, this generated arithmetic. The idea that in philosophy is the number at the base of the real world. Aristotle said: "It seems that the number is the basis, that is, the matter that forms real things, in the opinion of the Pythagoreans." The Pythagorean also worked in music and saw that by giving the quintet and octave of a base note in this field they were in fixed relationships of 6/4/3 length of a string. The idea that the basic entities were formed by definite and indivisible units, received from it a great help.
Then, based on this scheme of relative numbers, they wanted to build the whole theory of the Universe. These relative numbers corresponded to those indivisible space units. They consider that the distances between the planets and the Earth should follow a musical progression. This would create the "music of the spheres".
Being the sum of the first four numbers, the tenth was a perfect number, so the fusion bodies should also have ten. But as they only saw nine, they launched the hypothesis of an unforeseen "contralur". Aristotle criticized this dream with actions.
However, the Pythagoreans carried out the cosmogony. Most of what we know about it is known through the Filolao of the Kro ton. He lived in the middle of the fifth century BC. Somewhere, they realized that the Earth was spherical and the rotation of the apparent heavens was easier to express if the rotation of the Earth was accepted. This rotation of the Earth would not occur on its axis but on a fixed point of space, turning the contralura at the other end of the diameter.

However, as in this rotation the half that has the life of the Earth Sphere is always on the side of the external fusion, it is not possible to see the aforementioned crest. At the fixed point that is not seen would be on a great fire: the "altar of the universe". This idea led to the creation of a wrong eryte, of what the Pythagoreans established heliocentric theory before Aristarchus and Copernicus.
On the part of Kosmogonia Pitagora and her students abandoned the idea of a single material element to recognize that matter is formed by earth, water, fire and air. These elements represented a combination of four qualities per pair: heat, cold, humidity and dryness. Thus, while the water is cold and humid, the fire is hot and dry.
The first Pythagoras combined geometry with arithmetic. Pitagora imparted teaching based on abstraction, precise definitions and demonstrations. If we take into account the practical knowledge of Egypo and Mesopotamia, lines, points, etc. It is difficult to know when and where abstract ideas appeared; however, these achievements are traditionally added to the Pythagoreans and with them the creation of abstract geometry. This school showed, among other things, that the angles of a triangle form two straight angles or that on the side n the interior angles of a polygon of c (2n 4) serve as a right angle.
The best known achievement of the founder of this school is the theorem baptized as "Theorem of Pitagora": "The square built with the hypotenuse of a straight triangle is as much as if of the squares constructed by two other parts of that triangle" (Euklide, "Elements", I, 47).
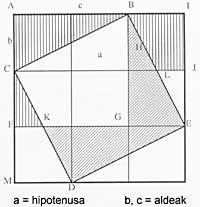
Plutarch, Diogene Laercio and Proklo affirm that this theorem was enunciated by Pitagora and that, apart from its original origin, apparently known to the Babylonians, is one of the deepest bases in the history of mathematics.
The mystical idea of Nature in the doctrine of numbers in this school demonstrates the importance that the Pythagoras had of the opposing elements: light and darkness, love and hatred, etc. This mystical idea reappeared in the doctor Alkmeon.
In this sense, man is a microcosm, that is, a small universe: while the body reflects the structure of the world, the soul is the harmony of the number.
If the Jonians defended the philosophy of matter, the Pythagoras challenged the philosophy of appearance. a.C. In the fifth century this last school was divided into two branches: one became a religious institution and the other developed a theory of almost scientific number.

Gai honi buruzko eduki gehiago
Elhuyarrek garatutako teknologia