Nombre de numéros

1989/02/01 Angulo, Patxi Iturria: Elhuyar aldizkaria

• Matematika

Ces ensembles sont représentés avec les lettres N, Z, Q, R, C respectivement, et accomplissent que chacun d'eux appartient au groupe suivant. Ceci est généralement dit mathématiquement N\ Z Q Q B C.

Mais tout cela est une simple théorie, car en réalité, dans la rue, les nombres les plus utilisés sont ceux du groupe Z et comme beaucoup ceux du groupe Q. En fait, les nombres type 1, 2, 1000, 3627 sont les plus utilisés et, pour ainsi dire, si nous voulons exprimer les dettes, nous mettons en avant les nombres (–) en négatif. Bien sûr, des nombres décimaux sont également utilisés. Exemple 2,13 m, 7,14 kg. 1,8 l, etc. Cependant, menuisiers, plombiers, etc. remplacent le mètre et le centimètre par millimètre en tant qu'unité au moment d'indiquer les mesures. Ainsi, les nombres décimaux deviennent simples: 2130 mm par exemple.

Cette utilisation des nombres naturels, en plus de donner son nom aux nombres, a conduit de nombreux mathématiciens à effectuer une analyse approfondie de la même et tant de personnes qui ne sont pas mathématiques. Le fruit de cet approfondissement est la théorie numérique. Cette théorie avec le mathématicien Fermat XVII. Nous pouvons dire qu'il est né au XIXe siècle. Dans ce siècle, précisément, a été publié le premier traité sur les Jeux Mathématiques écrit par le poète et cinéaste Claude-Gaspard Bachet et Méziriac: Problèmes plaisant détectables qui se font par les noms. En plus du jeu de cartes et de nombres connus à l'époque, on y trouvait des questions plus profondes. Entre autres, la construction de carrés magiques et des problèmes d'analyse illimités.

D'autre part, nous devons considérer comme fruit les résultats obtenus dans le domaine des jeux numériques, parfois profonds, nombres premiers, nombres amis, etc. et dans d'autres cas seulement curiosités. Nous continuerons sur cette dernière voie.

Pour commencer, pourquoi pas, nous prendrons le 142857 normal. Il donne un nombre réel et normal, comme tout autre. Cependant, ce n'est pas vrai. Multiplier ce nombre par les six premiers nombres naturels:

142857 x 1 = 142857
142857 x 2 = 285714
142857 x 3 = 428571
142857 x 4 = 571428
142857 x 5 = 714285
142857 x 6 = 857142

tous les produits ont les mêmes chiffres, en gardant l'ordre des chiffres comme si c'était un cycle. Si elle est également multipliée par 7:

142857 x 7 = 999.999

vous obtenez. Ce dernier résultat, avec un petit effort, peut nous amener à connaître la nature du nombre. Si on calcule l'expression décimale du nombre rationnel 1/7,

0,142857 142857 142857 142857 ... (0,142857 142857... x 7 = 0,99999999...)

On obtient, c'est-à-dire le numéro 142857 initial est la période du numéro 1/7.

D'autres nombres ont été trouvés avec les mêmes propriétés. Ces nombres sont appelés nombres cycliques. Entre autres, ceux générés par les numéros 17, 19, 23, 29, 47, 59, 61 et 97 mineurs de 100. Par exemple, le numéro 17 produit la fraction 1/17, étant sa période 0588235294117647. Si vous multipliez ce nombre par 1, 2, ..., 16, vous obtiendrez les mêmes chiffres; dans le même ordre, mais en commençant par un autre nombre (pas zéros):

0588235294117647 x 3 = 1764705882352941

Tous les nombres cycliques sont des périodes des fractions inverses de certains nombres premiers.

Laissons pour le moment les numéros cycliques et voyons d'autres numéros. De nombreux lecteurs connaissent probablement le numéro 12345679 et ses propriétés:

12345679 x 9 = 111 111 12345679
x 18 = 222 222
12345679 x 81 = 999 999 999

Cependant, nous ne savons pas si vous connaissez ou non que ce qui est ici accompli pour le numéro 9 peut être rempli dans d'autres numéros. Voici comment le faire. Nous calculerons comme exemple un autre pour le nombre 7. Nous le posons comme équation : nous voulons chercher le nombre x, qui multiplié par 7 nous donnera un nombre de 1 chiffres, c'est-à-dire :

x . 7 = 111 111 111 ... (on ne connaît pas le nombre de chiffres)

Donc pour chercher x il faut diviser le nombre 1111... par 7 jusqu'à ce que la division soit exacte.

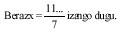
Si le calcul est effectué

Dans ce cas, le nombre de 1 chiffres a six chiffres. Cette méthode nous montre que pour le numéro 2 il n'est pas possible d'obtenir ce numéro (même pas pour les couples), car il n'est pas le numéro 111... et est divisible par le numéro 2.

Curieusement, le numéro 49 est le 2267573696145124716553287981859410430839.

Passons à un autre.

Prenez un nombre qui n'a pas tous les chiffres égaux. Nous avons choisi 8161. Ce que nous allons faire ici dans ce numéro, vous devez le répéter avec le numéro que vous avez avancé.

La même chose sera faite avec le numéro qui apparaît sur le compte

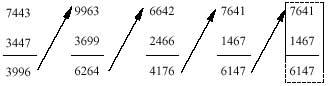
Quand est-ce que ça finit ? Dans la dernière déduction, on voit clairement quelle est la réponse. Si dans la dernière déduction la différence a les mêmes chiffres que le minuendo et le resteur, cela signifie que si les chiffres sont réarrangés, on obtiendra la même soustraction. Par conséquent, vous ne pouvez pas suivre.

Quoi ? Avez-vous eu la même chose avec votre numéro? Si nous ne nous trompons pas, vous avez obtenu le même numéro 6174, non?

Il en va de même pour les nombres à 3 chiffres

A la fin on obtient toujours le 495.

Nous vous laissons l'analyse des nombres à deux et cinq chiffres.

Pour finir nous dirons que les résultats que vous avez sous ces lignes ne méritent pas un autre nom que la curiosité. Dans le premier groupe toutes les multiplications les chiffres 1, 2, 3, 4, 5, 6, 7, 8 et 9 apparaissent une seule fois:

138 x 42 = 5796
157 x 28 = 4396
159 x 48 = 7632
186 x 39 = 7254
198 x 27 = 5346
297 x 18 = 5346
483 x 12 = 5796
1738 x 4 = 6952
1963 x 4 = 7852

Dans le deuxième groupe les carrés de certains numéros spéciaux:

1 ² = 1
11 ² = 121
111 ² = 12321
1111 ² = 1234321
11111 ² = 123454321 111111
² = 12345654321
111111
² = 1234567654321 1111 ² = 123456765874321 11111
^{2 2} = 12345676587654321

9 ^{2 2}