Numbers

1989/02/01 Angulo, Patxi Iturria: Elhuyar aldizkaria

• Matematika

These sets are represented with the letters N, Z, Q, R, C respectively, and each of them belongs to the next group. This is often said mathematically N\ Z Q Q B C.

But all this is a mere theory, since in reality, in the street, the most used numbers are those of group Z and at most those of group Q. In fact, the numbers type 1, 2, 1000, 3627 are the most used and, so to speak, if we want to express the debts, we put before the numbers (–) in negative. Of course, decimal numbers are also used. Example 2.13 m, 7.14 kg. 1.8 l, etc. However, carpenters, plumbers, etc. replace the meter and centimeter per millimeter as a unit when indicating the measurements. Thus, decimal numbers become simple: 2130 mm for example.

This use of natural numbers, in addition to naming numbers, has led many mathematicians to conduct a thorough analysis of them and so many people who are not mathematics. The fruit of this deepening is numerical theory. This theory with the mathematician Fermat XVII. We can say that it was born in the nineteenth century. In that century, precisely, the first treatise on Mathematical Games was published written by the poet and filmmaker Claude-Gaspard Bachet and Méziriac: plaisant detectable problems qui se font par les nombres. In addition to the game of cards and numbers known at that time, deeper issues were included. Among others, the construction of magic squares and unlimited analysis problems.

On the other hand, we must consider as fruit both the results obtained in the field of numerical games, sometimes deep, prime numbers, friend numbers, etc. and in other cases only curiosities. We will continue on this last path.

For starters, why not, we will catch the natural 142857. It gives a real and normal number, like any other. However, it is not true. Multiplying this number by the first six natural numbers:

142857 x 1 = 142857 142857 x 2 = 285714 142857 x 3 = 428571 142857 x 4 = 571428 142857 x 5 = 714285 142857 x 6 = 857142

all products have the same figures, keeping the order of the figures as if it were a cycle. If it is also multiplied by 7:

142857 x 7 = 999.999

is obtained. This last result, with a small effort, can lead us to know the nature of the number. If the decimal expression of the rational number 1/7 is calculated,

0,142857 142857 142857 142857 .. (0,142857 142857... x 7 = 0,99999999...)

is obtained, that is, the initial number 142857 is the period of number 1/7.

Other numbers with the same properties have been found. These numbers are called cyclic numbers. Among others, those generated by numbers 17, 19, 23, 29, 47, 59, 61 and 97 under 100. For example, number 17 produces fraction 1/17, its period being 0588235294117647. If you multiply this number by 1, 2, .., 16, you will get the same numbers; in the same order, but starting with another number (not zeros):

0588235294117647 x 3 = 1764705882352941

All cyclic numbers are periods of the reverse fractions of certain prime numbers.

Let's leave cyclical numbers for the moment and let's see other numbers. Probably many readers know the number 12345679 and its properties:

12345679 x 9 = 111 111 111 12345679 x 18 = 222 222 12345679 x 81 = 999 999 999 999

However, we do not know whether or not you know that what is fulfilled here for number 9 can be filled in other numbers. Here's how to do it. We will calculate another example for number 7. We propose it as an equation: we want to look for the number x, which multiplied by 7 will give us a number of 1 figures, that is:

x . 7 = 111 111 111 111 .. (we do not know the number of figures)

so to search x you have to divide the number 1111... by 7 until the division is accurate.

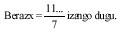
If the calculation is performed

In this case the number of 1 figures has six figures. This method shows us that for number 2 it is not possible to obtain this number (not even for pairs), since it is not number 111... and it is divisible by number 2.

As a curiosity, the number obtained for number 49 is 2267573696145124716553287981859410430839.

Let's move on to another.

Take a number that doesn't have all the same figures. We chose 8161. What we are going to do here in this number you must repeat it with the number you have advanced.

The same will be done with the number that appears in the account

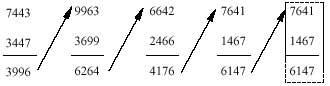
when does it end? The last deduction clearly shows what the answer is. If in the last deduction the difference has the same figures as the minute and the restator, this means that if the figures are reordered the same subtraction will be obtained. Therefore, it cannot be followed.

What? Has the same happened to you with your number? If we're not wrong, you've got the same number 6174, right?

The same goes for 3-digit numbers

In the end you always get the 495.

We leave for you the analysis of the numbers of two and five figures.

Finally, we will say that the results you have under these lines deserve no other name than curiosity. In the first group all multiplications figures 1, 2, 3, 4, 5, 6, 7, 8 and 9 appear only once:

138 x 42 = 5796 157 x 28 = 4396 159 x 48 = 7632 186 x 39 = 7254 198 x 27 = 5346 297 x 18 = 5346 483 x 12 = 5796 1738 x 4 = 6952 1963 x 4 = 7852

In the second group the squares of some special numbers:

1 2 = 1 11 2 = 121 111 2 = 12321 1111 2 = 1234321 11111 2 = 123454321 111111 2 = 12345654321 11111111 2 = 1234567654321 1111 2 = 12345676765874321 1111111 2 = 12345678678987654321

9 2