Chaîne d'or et...

1988/06/01 Angulo, Patxi Iturria: Elhuyar aldizkaria

• Matematika

Le jeu qui a créé de nombreuses rumeurs ces derniers temps est la chaîne d'or. On a déjà beaucoup parlé de ce jeu dans les médias, la télévision, les journaux, la radio. Nous relierons ici ce jeu avec les mathématiques.

Commençons par le développement du jeu et voyons comment 40.960.000 pesetas peuvent être gagnées. Nous supposons que la personne A achète une liste. Une fois la liste achetée, vous devrez verser 5000 pesetas à la première personne. Comme il a payé 5.000 pesetas supplémentaires pour la liste, il a pour le moment perdu 10.000 pesetas. Maintenant, vous devez supprimer le premier nom de la liste et le vôtre à la 12e place, à savoir écrire.

Cette nouvelle liste doit être vendue à deux personnes. Si ces deux sont B et C, ils auront sur leur liste le nom de A à la 12ème place (en ce moment A récupère 10.000 pesetas, donc il n'a rien perdu). Les personnes B et C doivent passer les listes à deux autres personnes, comme D, E, F et G. Dans les listes de ces quatre personnes nous trouverions le nom de A à la 11e place. Dans la prochaine étape 8 seront les personnes qui ont le nom de A à la 10ème place dans la liste. La prochaine fois 16 personnes auront le nom de A sur la 9ème place. Il n'est pas difficile d'estimer que le nombre de personnes qui ont le nom de A en première position est 4.096.

Ces derniers doivent vendre les listes à 8.192 personnes, dans toutes ces listes le nom de A est en 1ère position. Par conséquent, ces 8.192 personnes devront payer cinq mille pesetas pour acheter la liste, à savoir, A devrait facturer 8.192 x 5.000 = 40.960.00 pesetas (si tout va bien). En attendant de mieux suivre ce qui est exposé, la table est jointe avec toutes les étapes du processus:

Jusqu'ici, nous avons fait une description du jeu. Cette description montre une augmentation importante du nombre de personnes. À la fin de l'article, nous en parlerons ainsi que de grands nombres. Ici, nous avons mentionné les mots jeu et argent, et maintenant il nous est difficile de ne pas mentionner d'autres jeux de hasard que nous connaissons pour gagner de l'argent rapide.

Cette fois, nous allons procéder au calcul approximatif des probabilités de ces jeux.

Nous ne pouvons pas considérer la chaîne d'or comme un jeu de hasard. Quelle est la probabilité de vendre une liste? Je connais un ami qui a vendu les deux listes un jour, mais aussi un ami qui a passé deux semaines et n'a vendu aucune liste. Nous ne parlons donc pas de la probabilité de ce jeu, mais des autres.

Quinelles

Pour commencer, pourquoi pas, nous analyserons les cinq. Bien sûr, dans ce jeu le facteur humain a son importance, nous ne le nierons pas (1, X, 2 n'ont pas la même chance de sortir dans les matchs Real-Sabadell ou Osasuna-Atletia de Bilbao).

Mais du point de vue de la personne qui fait le pari, à chaque match nous pourrions mettre 1, X ou 2, en approchant seulement avec un, c'est-à-dire, la probabilité de réussir sera de 1/3. Chance de deviner deux matches 1/3 . 1/3 (première et deuxième). Par conséquent, ce serait la probabilité de réussir les 14 matches (le tout avec une colonne bien sûr).

Avec deux ou trois symboles augmentera la probabilité. Le plus grand pari multiple est de 5 triples et 2 doubles. Cela suppose 972 paris. Par conséquent, dans ce cas, la probabilité est de 0,0002032 (soit 4.921 paris seulement une chance). Comme vous pouvez le constater, bien que beaucoup de progrès aient été accomplis, la dixième partie n'a pas été atteinte et le montant à dépenser est de 19.440 pesetas (nous n'analyserons pas ici les développements abrégés).

Nous continuerons avec la loterie. Le facteur humain n'influence pas ce jeu. Il ya beaucoup de prix à la loterie, mais le plus grand ne correspond qu'à l'un des 80.000 numéros. Probabilité dans ce cas

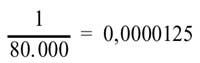
est, faible du tout. Il y a un prix appelé pedrea (comme nous le savons tous, si le dernier chiffre de votre numéro correspond au prix principal, ils vous renvoient ce que vous jouez). Étant donné que dans un tirage ordinaire il y a environ 1.200 prix (sans compter les finales), la probabilité d'obtenir un prix est de 0,015 (c'est à dire, seulement une chance sur 67), il n'est pas mal comparée à la quinilla.

Lotus

Le système de tirage au sort du lotus est totalement différent. Le joueur doit choisir 6 sur 49. Les chances d'être récompensé sont présentés dans le tableau suivant.

Ici, nous n'analyserons pas les cas où plusieurs paris sont placés sur un carré. (Dans le cas le plus simple, comme vous pouvez le constater, une seule des 1055 est à gagner).

Dans le nouveau jeu BONO-LOTO, les chances sont 4 fois plus grandes, car un même pari participe à 4 tirages. Elles seront les suivantes:

(Dans le cas le plus simple, 263 paris, il n'y a qu'une seule chance).

Tirage au sort des aveugles

Il n'y a que 5 prix dans le tirage du ONCE. Participent 100.000 numéros. La probabilité d'obtenir le prix principal est de ^1/10 5, soit 0,00001. La probabilité d'obtenir le deuxième prix (mais pas le premier) est de 9/10 ⁵ = 0,00009. La troisième (et non les deux ci-dessus) est obtenue avec une probabilité de 9/10 ⁴ = 0,9. Pour obtenir le quatrième (et non les précédents) la probabilité est de ^{9/10 3} = 0,009 et enfin la probabilité d'atteindre seulement le cinquième est de 9/10 ² = 0,09. (Si un prix est gagné, il faut garder à l'esprit que vous ne pouvez pas obtenir de prix inférieurs) Mais la probabilité d'obtenir au moins un prix est de 1/10 = 0,1 (ce qui correspond à la réussite du dernier chiffre).

Jusqu'à présent, nous avons dit ce qui concerne les probabilités de jeu connus. Comme vous le voyez, il n'est pas facile d'obtenir de l'argent avec ces méthodes.

Chaîne en or

Maintenant, et comme promis, nous allons parler de l'augmentation du nombre de personnes qui participent au jeu de la Chaîne d'Or et des grands nombres.

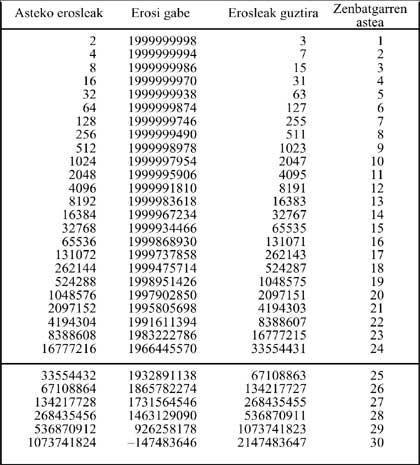
Supposons qu'une personne a besoin d'une semaine pour vendre deux listes. Dans l'État, l'achat de la liste devrait être de 20 millions d'habitants. Comme vous pouvez le voir dans la liste ci-dessous, à la semaine 23, 8.388.608 achèteraient une liste, restant 3.222.786 personnes sans liste, voir tableau original. La semaine suivante, il faudrait vendre 16.777.216 listes. Si nous nous assurons que chaque personne achète une seule liste, ils ne seraient pas amis pour acheter toutes les listes. C'est-à-dire,

Une liste a été utilisée pour indiquer. Mais il est surprenant de savoir que prenant la moitié de la population mondiale, soit 2 milliards de personnes, le jeu se terminerait par la semaine 29 (soit 6 semaines plus tard), comme vous pouvez le voir dans la liste ci-dessous.

Pour finir

Prenez maintenant un papier et ne dites pas plus ou moins combien de fois vous pouvez doubler. Essayez-le avec un folio. Avez-vous réussi ? Non ? Prenez une page plus grande, par exemple la double page du journal et réessayez. Combien de fois avez-vous plié? Supposons que l'épaisseur d'une feuille est de 0,001 cm.
Si nous plions la feuille une fois que nous obtenons l'épaisseur de deux feuilles. En repliant, l'épaisseur des quatre feuilles et de continuer ainsi, en les pliant à ^{50 fois nous obtiendrions l'épaisseur de 2 50} = 1.125.699.906.842.624 feuilles, c'est-à-dire :

c'est-à-dire, plus de onze millions de kilomètres d'épaisseur. Dans la pratique, il a été démontré qu'il peut être plié jusqu'à 8 fois. Si nous parlons de grands nombres, nous allons poser deux questions pour terminer l'article: combien de temps faut-il pour compter un million de nombres à partir de 1 (un, deux, ...)? et compter un milliard ? (Calculez les chiffres que vous comptez en une minute).