Loto-ri buruzko jolasak
1986/08/01 Goñi, Jesus Mari | Etxeberria, J. Iturria: Elhuyar aldizkaria
Alizia oporretan kanpora joan zaigunez, oraingoan beste joku-mota bat izango da gure idazlaneko gai.
Azkeneko hilabetetan, Estatuan loto jokoa ezartzearen hasiera ikusi dugu. Martxan jarri bezain laster, jendeak itxaropen handiz onartu du. Aldizkariak, egunkariak... eta beste zenbait publikazio loto-ri buruzko artikuluez beterik daude.
Artikulu eta atal hauek, sistema laburraz mintzatzen dira, eta nahiz eta zehazki ez esan, apostulariei zera sinesterazi nahi zaie: boleto horiek betetzeko zenbait era ezberdin badela, eta aterako diren zenbakiei igarrita, dirua erraz eskura daitekeela.
Loto, zorizko jokoa (aleatorioa) dela esan behar da eta aterako diren zenbakiak aurrez jakiteko bide egokirik ez dagoela.
Hau esan ondoren, ez dizuegu zenbakiak asmatzeko bide egokirik emango, eta... dena dela, bide hori edukiko bagenu ere, ez genizueke azalduko. Ulertzen duzue zergatik, ezta?
Baina dena dela, loto-ri buruz azterketa txiki batzuk egitea nahi dugu. Lehendabizi, zein probabilitate daukagu sei zenbakiak asmatzeko, bost hogerleko jokatzen ditugunean?
Dakigunez, probabilitatearen definizio klasikoak A-gertakizun baten probabilitatea era honetara ematen digu:
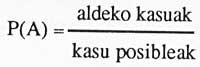
Gure apostuan sei zenbakiak asmatzeko aldeko kasuak bat dira. Eta... zenbat dira kasu posibleak?
Arazoa ez da zaila, zeren eta dakigunez 49 zenbakietatik, sei aukeratu behar dituzu eta seiak asmatu.
Eta sei zenbaki ezberdinak irteteko kasu posibleak, honela lortuko dira: 49 zenbaki hauekin 6nakako taldeen konbinazioak eginaz. Hau da, 49 zenbakizko multzo baten, 6 zenbakizko azpimultzo guztiak izango dira:
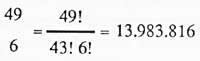
Beraz, asmatzeko probabilitatea zera da:
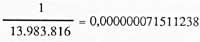
Ez zaigu oso handia atera, ezta? Baina hala eta guztiz ere, 200 milioi gureganatzen baldin baditugu? Beno, denak helduak gara eta bakoitzak ikusiko du.
Gure kalkuluak egiterakoan, zera beharko genuke izan kontutan: loto, gabonetako loteriaren sistema berdinekoa dela. Baina gabonetan gehienez 100.000 zenbaki banatzen badira, loto-n 13.983.816 zenbaki banatzen dira. Aldatzen dena, noski, sarien banaketa da.
Eta oraindik gabonetako loteriaz mintzatzen diren sistema laburtuak ez ditugu behin ere ikusi!
Loto-ri buruz hitz egiten hasi garenez, joko honi buruz buruhauste batzuk proposatu nahi dizkizuegu.
Buruhauste hauek, tabernan entzundako elkarrizketa baten ondoren egindakoak dira.
Han zegoen zenbait neska-mutil berriketan, eta lehenengoz honako hau entzun genuen:
Ez dakit nola bete nuen loto-txartel hau, baina joan zen astean ez nuen zenbaki bat ere asmatu... zaila da gero eh! Ez dakit kasu hauetan zergatik ez duten saririk ematen.
(1) Guk: Zein da zenbaki bat bera ere ez asmatzeko dugun probabilitatea?
Pellok hau esan zuen: Nik, zenbaki bikoitiak irteten direla gehien uste dut. Begira aurreko astean ere, sei zenbakietatik bost bikoitiak ziren... Datorren astean nik, denak bikoitiak ipini behar ditut.
(2) Guk: Zein da sei zenbakiok bikoitiak izateko probabilitatea?
Zerbitzariak ere parte hartu eta zera esan zuen:
Egia dena zera da: zenbakiak zifra desberdinez bukatzen direla. Aurreko astekoak hartzen baditugu: 2, 6, 3, 4, 0 eta 8az bukatu ziren.
Guk: Zein da 6 zenbakiok zifra desberdinez bukatzeko probabilitatea?
Ikusten dugunez, denek zuten zerbait esateko. Joxe orduantxe ailegatu zen, eta berak honako hau bota zigun.
Segidako bi astetan, gutxienez zenbakiren bat errepikatzen da.
(4) Guk: Zein da Joxek esan duena gertatzeko probabilitatea?
(5) Azkenik, arazo hau azaltzen dizuegu. 6 zenbaki aukeratu behar dituzu, baina ondoko baldintzak kontutan harturik, eta noski, kontutan hartu bost hogerleko dauzkazula.
- Zenbaki lehenik (primorik) ez dadila egon
- Loto-ko 6 zenbaki aukeratzerakoan, 10 zifrak erabiltzea, eta zifra bakoitza gehienez behin bakarrik erabiltzea.
- Zenbaki bat aukeratu ondoren, ezin duzu bere ondoko laukitxoetan dagoenik ipini.
- Azkeneko baldintza, bi eratara uler daiteke.
"Ondoko laukitxoak" alde amankomun bat daukatenak badira, guk 6 ebazpen lortu ditugu.
"Ondoko laukitxoak" puntu amankomun bat daukatenak badira, guk ebazpen bakarra lortu dugu.
Beno, orain zuen esku geratzen da... Ah! eta gutxi gastatu!

Gai honi buruzko eduki gehiago
Elhuyarrek garatutako teknologia